Όταν το ελατήριο έχει μάζα

• Δημοσιεύτηκε από τον/τηνΚορφιάτης Ευάγγελος στις 12 Νοέμβριος 2011 και ώρα 1:30

Αφορμή για την παρούσα ανάρτηση ήταν η θέση που διατύπωσε ο Γιάννης ο Κυριακόπουλος όσον αφορά στην συχνότητα ταλάντωσης ενός σώματος, το οποίο είναι δεμένο σε ελατήριο όχι αμελητέας μάζας.

Το συνηθισμένο αποτέλεσμα για την γωνιακή συχνότητα της ταλάντωσης του σώματος είναι:

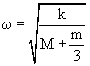
όπου M η  μάζα του σώματος, m η μάζα του ελατηρίου και k η σταθερά του ελατηρίου.

Σημαντικός προβληματισμός μου όσον αφορά το αποτέλεσμα αυτό ήταν το γεγονός ότι δεν μπορούσα να επαληθεύσω εκ των υστέρων την σχέση

ΣF=-Μω²x για το σώμα.

Βασική άποψη ήταν ότι πρέπει να μελετήσει κανείς τόσο την κίνηση του σώματος όσο και τα διαμήκη κύματα που διαδίδονται στο ελατήριο.

Η ορθή σχέση για τον θεμελιώδη τρόπο ταλάντωσης είναι:

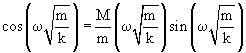
Στην σύντομη αυτή πραγματεία κατ’ αρχάς εξάγεται (ως υπενθύμιση) η εξίσωση των διαμήκων κυμάτων σε ένα γραμμικό ελαστικό μέσο και εφαρμόζεται στην περίπτωση ενός ελατηρίου.

Στην συνέχεια ανευρίσκονται οι κανονικοί τρόποι ταλάντωσης του συστήματος ελατήριο – μάζα τόσο στην περίπτωση που το ελατήριο είναι οριζόντιο όσο και στην περίπτωση που το ελατήριο είναι κατακόρυφο.

Τέλος εξετάζεται βήμα το βήμα η κίνηση του σώματος.

Η συνέχεια στο Blogspot ή σε  ή σε 

Τα σχόλια

Σχόλιο από τον/την Κυριακόπουλος Γιάννης στις 12 Νοέμβριος 2011 στις 10:47

Βαγγέλη θα το μελετήσω.

Πριν διαβάσω οτιδήποτε (εκτεταμένη γαρ μελέτη) βλέπω μια σχέση παραπάνω όπου το αριστερό σκέλος παίρνει τιμές μικρότερες της μονάδας. Το δεξιό;

Το θέμα το γνώρισα από τον Βαγγέλη Κουντούρη ο οποίος επιβεβαίωσε πειραματικά.

Σχόλιο από τον/την Κορφιάτης Ευάγγελος στις 12 Νοέμβριος 2011 στις 13:11

Μια απολογία και μια διευκρίνιση

Η ακριβής σχέση που δίνει την συχνότητα του θεμελιώδη τρόπου ταλάντωσης μπορεί να πάρει την απλούστερη μορφή

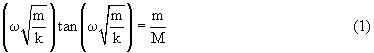
Η σχέση που προτείνουν οι Κυριακόπουλος Γιάννης και Κουντούρης Βαγγέλης είναι

Κάνοντας λάθος στον αριθμητικό υπολογισμό της δεύτερης όταν m=M μου προέκυπτε ότι τα δύο αποτελέσματα ήταν ριζικά διαφορετικά.

Αναπτύσσοντας κατά Taylor την πρώτη στην περίπτωση που mM η δεύτερη έβγαινε προσέγγιση της πρώτης.

Όμως, υπολογίζοντας τις δύο συχνότητες αριθμητικά για διάφορες τιμές του λόγου σ=m/M διαπίστωσα ότι για m<=M σχεδόν συμπίπτουν.

Ας θέσουμε

και ω₁, ω₂ της συχνότητες που προκύπτουν από τις σχέσεις (1) και (2).

σ=0.5               ω₁=0.653ω₀                 ω₂=0.654ω₀

σ=1                  ω₁=0.860ω₀                 ω₂=0.866ω₀

σ=5                  ω₁=1.313ω₀                 ω₂=1.369ω₀

σ=10                ω₁=1.428ω₀                 ω₂=0.1519ω₀

Επομένως όταν η μάζα του ελατηρίου είναι μικρότερη ή ίση της μάζας του σώματος, τότε η σχέση (2) είναι ακριβής.

Όταν m>10M οι δύο σχέσεις αποκλίνουν.

Σχόλιο από τον/την Κυριακόπουλος Γιάννης στις 12 Νοέμβριος 2011 στις 16:03

Βαγγέλη όχι φυσικά προτείνουμε εμείς. Το ανέφερε ο Βαγγέλης , εξετέλεσε το πείραμα και αλληλογραφήσαμε (πριν 7 νομίζω χρόνια). Τώρα είδα ότι και η Βικιπέδεια το αναφέρει με απλουστευμένη απόδειξη.

Σκαλίζοντας τα ηλεκτρονικά κιτάπια μου βρίσκω ότι ο Βαγγέλης χρησιμοποίησε ελατήριο 150 g , σώματα της τάξης του kg και το πείραμα είχε υπολογίσει effective mass (ενεργός μάζα;; , δρώσα μάζα;;) 50 g.

Σχόλιο από τον/την Κορφιάτης Ευάγγελος στις 12 Νοέμβριος 2011 στις 16:50

Γιάννη ευχαριστώ για την συμμετοχή στην συζήτηση.

Σε κάθε περίπτωση μάθαμε από σας τι γίνεται όταν το ελατήριο έχει μάζα.

Είναι εντυπωσιακή η ταύτιση των αποτελεσμάτων που δίνουν οι δύο σχέσεις όταν m<=M.

Με τα πειραματικά δεδομένα που αναφέρεις ισχύει ότι

ω1=0,35349ω₀ και ω2=0,35353ω_{0 .}

Θα είχε ενδιαφέρον να δούμε τι λέει το πείραμα για μεγάλες μάζες ελατηρίου (m>10M).

Αυτό που με ενοχλεί στην απλουστευμένη απόδειξη είναι το γεγονός ότι θεωρείται δεδομένο το γεγονός ότι το σώμα κάνει α.α.τ.

Αν δεν λάβεις υπόψη τα κυματικά φαινόμενα δεν μπρείς να επιβεβαιώσεις την συνθήκη της απλής αρμονικής ταλάντωσης.

Σχόλιο από τον/την Διονύσης Μάργαρης στις 12 Νοέμβριος 2011 στις 18:11

Βαγγέλη να σε ευχαριστήσω για την παραπάνω μελέτη που μοιράστηκες μαζί μας. Η αλήθεια είναι ότι θέλει μελέτη και σε πρώτη ευκαιρία, θα της  αφιερώσω χρόνο. Το σημαντικό νέο, που βάζει στην συζήτηση, είναι τα διαμήκη κύματα που διαδίδονται κατά μήκος του ελατηρίου που ομολογώ ότι είναι η πρώτη φορά που το συναντώ και το οποίο, (εκ των υστέρων βέβαια) είναι κάτι πολύ λογικό, αλλά που τουλάχιστον εγώ, δεν το είχα ποτέ σκεφτεί…

Σχόλιο από τον/την Κυριακόπουλος Γιάννης στις 12 Νοέμβριος 2011 στις 18:14

Για να γίνει το πείραμα που λες πρέπει να χρησιμοποιήσουμε το μαύρο ελατήριο που έχει σταλεί στα Λύκεια μήκους 4m κρεμασμένο από το μπαλκόνι του 1ου ορόφου , σώμα περί τα 100g και αισθητήρες.

Εκτός από το μαύρο υπάρχει και το τεράστιο ελατήριο στο οποίο η ταχύτητα των κυμάτων είναι πολύ μικρή. Αν το κρεμάσουμε από τον δεύτερο όροφο με μια μικρή μάζα η ταλάντωση θα έχει περίοδο της ίδιας τάξης με τον χρόνο που χρειάζεται το κύμα να διασχίσει το ελατήριο. Τι θα βλέπαμε;

Σχόλιο από τον/την Φιορεντίνος Γιάννης στις 12 Νοέμβριος 2011 στις 19:13

Βαγγέλη πολλά συγχαρητήρια για τη μελέτη σου. Όπως προανέφερε ο Διονύσης είναι η πρώτη φορά που συναντώ και εγώ τα διαμήκη κύματα να “συμμετέχουν” στην λύση του προβλήματος. Πολύ σπουδαία η σημείωση στο τέλος της εργασίας. Επίσης να ρωτήσω και κάτι: θεωρώντας και ανώτερους τρόπους ταλάντωσης σημαίνει ότι αυξάνονται οι βαθμοί ελευθερίας του συστήματος;

Σχόλιο από τον/την Κυριακόπουλος Γιάννης στις 12 Νοέμβριος 2011 στις 21:32

Γιάννη διαισθητικά πίστευα πάντοτε πως ναι. Έχει περισσότερους βαθμούς ελευθερίας.

Στέλνω δυο προσομοιώσεις-μοντελοποιήσεις όπου φαίνεται ότι διαφορετικές αρχικές συνθήκες οδηγούν σε εκδήλωση ή όχι της συνύπαρξης συχνοτήτων.

Με αρχική ταχύτητα.

Χωρίς αρχική ταχύτητα.

Φυσικά δεν είμαι απόλυτα σίγουρος μια και δεν μπορώ να κατασκευάσω συνεχές μέσο και οι μοντελοποιήσεις αυτές με έχουν κρεμάσει στο παρελθόν. Ταιριάζει πάντως αυτό που φαίνεται με την εικόνα του μικρού -χοντρού ελατηρίου όταν δεν κρεμάς κάτι σ’ αυτό.

Σχόλιο από τον/την Φιορεντίνος Γιάννης στις 12 Νοέμβριος 2011 στις 21:35

Γιάννη καλησπέρα.

Αυτό που σκέφθηκα διαβάζοντας την εργασία του Βαγγέλη, ήταν ότι τελικά ένα τέτοιο σύστημα θα πρέπει να έχει (θεωρητικά) άπειρους βαθμούς ελευθερίας.

Σχόλιο από τον/την Κυριακόπουλος Γιάννης στις 12 Νοέμβριος 2011 στις 21:44

Ναι αλλά για να εκδηλωθούν θα πρέπει να ευνοήσουν κατάλληλες αρχικές συνθήκες π.χ. τμήματα του ελατηρίου να “βληθούν¨με διαφορετικές ταχύτητες.

Αν η μάζα του κρεμασμένου σώματος είναι μεγάλη η ταλάντωσή του είναι κατά προσέγγιση αρμονική ενώ του ελατηρίου όχι.