Γεια σας Νίκο και Βασίλη,καλο καλοκαιρι. Νίκο πολυ ωραια ασκηση και δυσκολη.Μια διαφορετικη διατυπωση λυσης που βασιζεται στον χρονο κινησης αλλα που μπορει να την καταλαβει μονο μαθητης θετικης ειναι η εξης: Νικο αναφερομαι στο σχημα που βλεπω στην λυση σου:
Τελευταία διόρθωση6 μήνες πριν από Διονύσης Μάργαρης
Καλησπέρα!
Κωνσταντίνε και Βασίλη σας ευχαριστώ για τις λύσεις που αναρτήσατε.
Αν και εκτός ύλης νομίζω ότι αξίζει κάποιος να ασχοληθεί αφού το αποτέλεσμα ειναι μια ανταμοιβή που προσφέρει κάθε άσκηση με στροφορμή!
Ιδιαίτερο το θέμα σου Νίκο και η λύση σου επίσης μιας και ξεκινάς από από τις αντίθετες συνιστωσες της στροφορμής στο Γ ως προς το Ο .
Ενδιαφέρουσες και οι υπόλοιπες λύσεις.
Ανεβάζω μια διαφορετικη λύση ξεκινώντας από το ότι LΓ(Ο)=0 άρα η υ(Γ) διέρχεται από το Ο …..
Κώστα καλησπέρα!
Γνωρίζω ότι είσαι “συλλέκτης” καλών ασκήσεων τις οποίες λύνεις με το δικό σου τρόπο!
Σε ευχαριστώ πολύ! Λείπει νομίζω μια λύση αμιγώς γεωμετρική από τον Γιάννη Κυριακόπουλο αλλά μάλλον ειναι διακοπές!
Καλησπέρα Νίκο.Αν θεωρήσουμε ότι ο φορέας της ταχύτητας οποιαδήποτε στιγμή τέμνει τον φορέα της αρχικής στο Β’ όπου ισχύει (ΒΒ’)=(ΔΓ)/2 (κλασικό ζήτημα) τότε το θέμα ανάγεται σε αμιγώς γεωμετρικό.Τα τρίγωνα ΟΒΒ’ και ΟΔΓ είναι όμοια.Άρα R/(BB’)=R+(ΒΔ)/(ΔΓ) έτσι R/(BB’)=R+y/2(BB’) οπότε y=R.
Τελευταία διόρθωση6 μήνες πριν από Θυμιος Τσιτζηρας
Μία ακόμη λύση από τον Παναγιώτη Χριστάκο.
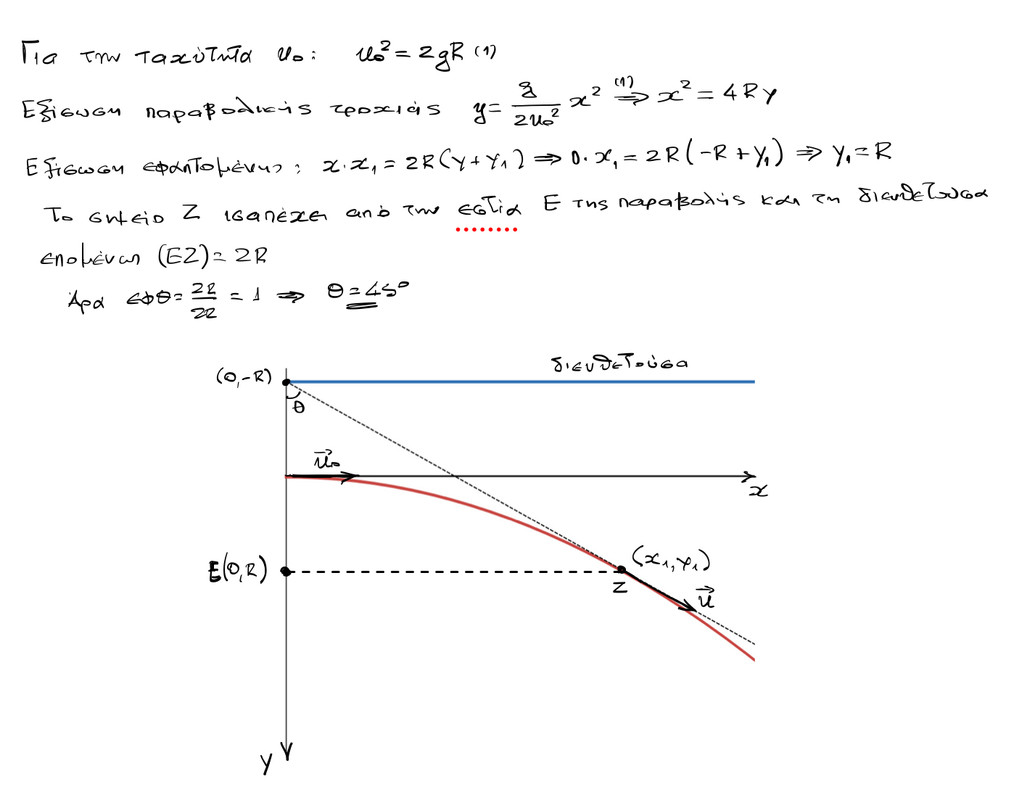
Γεια σας Νίκο και Βασίλη,καλο καλοκαιρι. Νίκο πολυ ωραια ασκηση και δυσκολη.Μια διαφορετικη διατυπωση λυσης που βασιζεται στον χρονο κινησης αλλα που μπορει να την καταλαβει μονο μαθητης θετικης ειναι η εξης: Νικο αναφερομαι στο σχημα που βλεπω στην λυση σου:
Καλησπέρα!
Κωνσταντίνε και Βασίλη σας ευχαριστώ για τις λύσεις που αναρτήσατε.
Αν και εκτός ύλης νομίζω ότι αξίζει κάποιος να ασχοληθεί αφού το αποτέλεσμα ειναι μια ανταμοιβή που προσφέρει κάθε άσκηση με στροφορμή!
Kαλησπέρα. Πράγματι ωραία ασκηση.Μια επιπλεον λυση
Ευχαριστώ πολύ Γιώργο για τη λύση σου και το σχολιασμό!
Καλημέρα .
Ιδιαίτερο το θέμα σου Νίκο και η λύση σου επίσης μιας και ξεκινάς από από τις αντίθετες συνιστωσες της στροφορμής στο Γ ως προς το Ο .
Ενδιαφέρουσες και οι υπόλοιπες λύσεις.
Ανεβάζω μια διαφορετικη λύση ξεκινώντας από το ότι LΓ(Ο)=0 άρα η υ(Γ) διέρχεται από το Ο …..
Κώστα καλησπέρα!
Γνωρίζω ότι είσαι “συλλέκτης” καλών ασκήσεων τις οποίες λύνεις με το δικό σου τρόπο!
Σε ευχαριστώ πολύ! Λείπει νομίζω μια λύση αμιγώς γεωμετρική από τον Γιάννη Κυριακόπουλο αλλά μάλλον ειναι διακοπές!
Καλησπέρα Νίκο.Αν θεωρήσουμε ότι ο φορέας της ταχύτητας οποιαδήποτε στιγμή τέμνει τον φορέα της αρχικής στο Β’ όπου ισχύει (ΒΒ’)=(ΔΓ)/2 (κλασικό ζήτημα) τότε το θέμα ανάγεται σε αμιγώς γεωμετρικό.Τα τρίγωνα ΟΒΒ’ και ΟΔΓ είναι όμοια.Άρα R/(BB’)=R+(ΒΔ)/(ΔΓ) έτσι R/(BB’)=R+y/2(BB’) οπότε y=R.
Καλησπέρα Θύμιο! Σε ευχαριστώ πολύ για το σχόλιο σου στην ανάρτηση μου!