by 
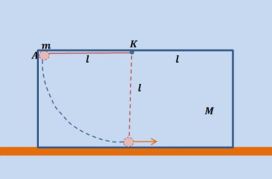
Κενό κιβώτιο μάζας Μ , διαστάσεων l×l×2l βρίσκεται πάνω σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή οριακής τριβής μ=0,25. Από το κέντρο Κ της οροφής του, έχουμε δέσει με νήμα , μη εκτατό ,αμελητέας μάζας και μήκους l , σώμα μάζας m=Μ αμελητέων διαστάσεων. Αφήνουμε το σώμα m από τη θέση Α να κινηθεί. Η αντίσταση του αέρα θεωρείται αμελητέα και το κιβώτιο δεν ανατρέπεται.
Η μηχανική ενέργεια που μετατράπηκε σε θερμική λόγω τριβών, είναι ίση με
Α)σχεδόν mgl B) 0,5mgl Γ) 0,86mgl Δ) μηδέν
Ποια σχέση είναι η σωστή;
η απάντησή μου(;)
Πρόδρομε μία ερώτηση: Στην λύση σου θεωρείς πως την μόνιμη, τελική κατάστασή του, το σύστημα την αποκτά όταν το εκκρεμές βρίσκεται σε ακραία θέση;
Γενικά έχω την εντύπωση ότι η λύση κοντά στα 0,86mgl είναι σωστή ως προσέγγιση αν η ποσότητα Lω2/g είναι πολύ μικρότερη της μονάδας (L το μήκος του νήματoς και ω η γωνιακή ταχύτητα του εκκρεμούς).
Η προσομοίωση που έκανα δείχνει αρχική ενέργεια μπαλακίου 160 J και 0 του κουτιού.
Στο τέλος έγινε 22,8 J του κρεμασμένου και μηδέν του κουτιού.
Απώλειες 137,3J ή ποσοστό 85%.
Το 74% και κάτι ψιλά, προκύπτει μεταξύ αρχής και της στιγμής που το νήμα είναι κατακόρυφο.
Οπότε περιμένω τη λύση για να καταλάβω τι συνέβη.
Γιάννη δεν καταλαβαίνω, από την στιγμή που σταματήσει το κιβώτιο, η απώλεια ενέργειας θα είναι μία και όταν το νήμα είναι κατακόρυφο και όταν βρίσκεται σε ακραία θέση (το εκκρεμές ταλαντώνεται χωρίς απώλειες στο εσωτερικό του κιβωτίου).
Καλά το λες Στάθη. Όμως πότε σταματάει το κιβώτιο;
Μάλλον εδώ:
Η αρχική μηχανική ενέργεια είναι 160 J. Αυτή είναι κάπου 22,8 J.
Δες όμως την εικόνα την πρώτη φορά που το νήμα γίνεται κατακόρυφο:
Η μηχανική ενέργεια είναι κάπου το 24,5% των 160J και όχι το 15%.
Μετά το σταμάτημα κάποια στιγμή το νήμα είναι κατακόρυφο:
Η ενέργεια είναι κάπου 15% της αρχικής. Απώλειες 85%.
Γιάννη εξακολουθώ να μην καταλαβαίνω. Την πρώτη φορά που το νήμα είναι κατακόρυφο δεν έχει σταματήσει το κιβώτιο, για αυτό η απώλεια δεν είναι η ζητούμενη. Όταν σταματήσει το κιβώτιο χάνεται επιπλέον ενέργεια, εξού και το 15% της αρχικής. Αυτό καταλαβαίνω ότι βγάζει το ip.
Το θέμα είναι μόλις σταματήσει το κιβώτιο, σε ποια θέση βρίσκεται το σφαιρίδιο και τι ταχύτητα έχει; Είναι καλή προσέγγιση να υποθέσουμε ακραία (μηδενικής ταχύτητας) την θέση του; Αυτό εξαρτάται από το μήκος του νήματος και τις μάζες.
Κάνω μια υπόδειξη της λύσης παραπάνω, στο τέλος της εκφώνησης. Όποιος θέλει να την προσπαθήσει , ας μη τη δεί.
Η προυπόθεση που έθεσα είναι ότι, στην τελευταία ταλάντωση τα σώματα ακινητοποιούνται ταυτόχρονα, κάτι που νομίζω ότι πρέπει να ισχύει.
Καλό σας βράδυ…
καλησπέρα σε όλους
θεωρώ ότι πολύ δύσκολο το θέμα
βλέπω ότι η κίνηση του κιβωτίου θα πάψει όταν το σφαιρίδιο βρεθεί σε max γωνία φ, τέτοια ώστε η οριζόντια συνιστώσα της τάσης του νήματος να είναι όση η οριακή τριβή, η αντίδραση του δαπέδου είναι τότε το βάρος του κιβωτίου συν την κατακόρυφη συνιστώσα της τάσης του νήματος
πολλή η τριγωνομετρία όμως
η απώλεια ενέργειας είναι, τότε, όση η μείωση της δυναμικής ενέργειας του σφαιριδίου
Μάλλον η λύση που αναφέρθηκε από τον Γιάννη Μήτση και τον Πρόδρομο (αν κάνω λάθος μου το λέτε) είναι η παρακάτω.
Στο σχήμα του Προδρόμου (T η τάση του νήαμτος, Τολ η τριβή ολίσθησης, Ν η κατακόρυφη δύναμη από το έδαφος):
Καταλαβαίνω ότι στέκει σαν λύση μόνον αν το κιβώτιο ακινητοποείται με το σφαιρίδιο στην ακραία θέση, ή αν ισχύει ότι ω2<<g/l. Ακόμη αν η μέγιστη γωνία στην μόνιμη κατάσταση είναι πολύ μικρή (δεν ισχύει για την τιμή συν(φ)=0.86)
Τώρα βλέπω πως την ίδια λύση μάλλον πρότεινε και ο Βαγγέλης.
(Έχω μπλέξει με τα σχήματα, δεν μπορώ πλέον να τα ανεβάσω μέσω imgbb, συγγνώμη για την ταλαιπωρία)
Παιδιά δεν έχω λύσει το πρόβλημα.
Οι προσομοιώσεις δείχνουν δύο πράγματα:
Δεν ξέρουμε αν το κιβώτιο σταματάει όταν το εκκρεμές είναι σε ακραία θέση.
ναι Στάθη, έτσι σκέφτηκα
το σφαιρίδιο στη μέγιστη φ, δεχόμαστε στιγμιαία ακινησία του κιβωτίου, δέχεται από το νήμα (άρα και ασκεί, ουσιαστικά στο άνω άκρο του, δηλαδή στο κιβώτιο) δύναμη mgσυνφ, η οποία αναλύεται σε οριζόντια mgσυνφημφ ίση με την τριβή μΝ και σε κατακόρυφη mgσυνφσυνφ
Ν=Μg+mgσυνφσυνφ, ΔΕ=mgh, h=l(1-συνφ)