by 
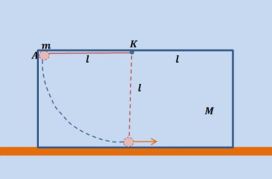
Κενό κιβώτιο μάζας Μ , διαστάσεων l×l×2l βρίσκεται πάνω σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή οριακής τριβής μ=0,25. Από το κέντρο Κ της οροφής του, έχουμε δέσει με νήμα , μη εκτατό ,αμελητέας μάζας και μήκους l , σώμα μάζας m=Μ αμελητέων διαστάσεων. Αφήνουμε το σώμα m από τη θέση Α να κινηθεί. Η αντίσταση του αέρα θεωρείται αμελητέα και το κιβώτιο δεν ανατρέπεται.
Η μηχανική ενέργεια που μετατράπηκε σε θερμική λόγω τριβών, είναι ίση με
Α)σχεδόν mgl B) 0,5mgl Γ) 0,86mgl Δ) μηδέν
Ποια σχέση είναι η σωστή;
η απάντησή μου(;)
Παρατηρώντας την εξέλιξη βλέπω πως ο ρυθμός απωλειών μειώνεται δραματικά με τον χρόνο. Έτσι αν υποθέσουμε ότι βρίσκεται σε ακραία θέση το εκκρεμές, το όποιο λάθος είναι ελάχιστο.
Γιάννη, αναρωτιέμαι (για την τελευταία σου πρόταση), μπορεί όταν το σφαιρίδιο ακινητοποιείται, το κιβώτιο να έχει ορμή; ποια δύναμη του την έδωσε
Καλημέρα Βαγγέλη, Γιάννη, Στάθη και όσοι μας διαβάζετε!!
Δυστυχώς κάνω λάθος σε πράξεις! Αρχικά έβαλα 0,744mgl , ενώ ήταν 0,86mgl. Γράφοντας τη λύση είπα να αποδείξω ότι :μετά τη θέση που η οριακή στατική τριβή, εξισώνεται με την συνιστώσα της τάσης του νήματος, και θεωρώντας από τη θέση αυτή όπου εφθ=2+(-)ρίζα(2) ,
το κιβώτιο δεν ολισθαίνει για οποιαδήποτε γωνία θ'<θ , υπολόγισα ότι αυτό δεν ισχύει, παρά για πάρα πολύ μικρές γωνίες.
Καταλήγω στο συμπέρασμα ότι η απώλεια ενέργειας είναι πολύ μεγάλη(!!!), και ότι στις θέσεις που το σφαιρίδιο σταματά ως προς το έδαφος, μπορεί το κιβώτιο να μη σταματά, ή και αντίστροφα .
Ίσως με μεγαλύτερο συντελεστή τριβής ή άλλη σχέση μαζών, να αποδεικνύεται ότι κάποια στιγμή το κιβώτιο δεν ολισθαίνει , ενώ το σφαιρίδιο ταλαντώνεται με την μηχανική ενέργεια που έχει απομείνει στο σύστημα.
Πάντως σας ευχαριστώ που ασχοληθήκατε με το πρόβλημά μου και καταθέσατε τις απόψεις σας!
Να είστε καλά.
Καλημέρα παιδιά.
Μια προσομοίωση:
Παλινδρομεί μέχρι να σταματήσει. Δεν είναι απλό θέμα.
Βαγγέλη λέγοντας “το κιβώτιο σταματάει” εννοώ τελείως.
Φαίνεται πως το κιβώτιο σταματάει όταν η σφαίρα δεν είναι σε ακραία θέση.
Δύο στιγμιότυπα:
Το κιβώτιο μένει ακίνητο από το αριστερό στιγμιότυπο ως το δεξί.
Μετά όμως τίθεται πάλι σε κίνηση.
Δηλαδή με πιο απλά λόγια, αν ακινητοποιηθεί το κιβώτιο δεν σημαίνει αυτό ότι σταμάτησε εσαεί και ότι έληξαν οι απώλειες ενέργειας.
Στάθη και Βαγγέλη ας δεχθώ την επόμενη σχέση:
Όμως αν ο συντελεστής τριβής είναι 1 τότε οι απώλειες είναι μηδενικές.
Το κιβώτιο δεν τίθεται σε κίνηση.
Γιάννη δεν θεωρώ ότι η λύση είναι αυτήν της σχέσης που έγραψα. Στην καλύτερη περίπτωση είναι μια προσέγγιση, έχω γράψει πότε θεωρώ ότι ισχύει. Έγραψα αυτήν την λύση από τις περιγραφές των φίλων για τις λύσεις τους και μάλιστα ρώτησα αν αυτό εννοούν.
Υπάρχει και ένα σημείο που απέκρυψα, η συγκεκριμένη εξίσωση
μ m + μ m συν2(φ)=m συν(φ) (1-συν2(φ))1/2
έχει δύο ρίζες για μ=0.25, την συν(φ)=0.86 ή φ=30ο και την συν(φ)=0.28 ή φ=74ο
Θεωρώ πως το πού θα βρίσκεται το σφαιρίδιο όταν ακινητοποιηθεί το κιβώτιο εξαρτάται από την συχνότητα αιώρησής του, δηλαδή από τις μάζες και το μήκος του νήματος. Σε αυτό το συμπέρασμα οδηγούν οι διαφορικές της κίνησης. Άλλαξε τις τιμές αυτών των μεγεθών στο ip που ανάρτησες και θα φανεί αμέσως.
Δεν νομίζω ότι λύνεται αναλυτικά αυτό το πρόβλημα.
Πιστεύω Στάθη και εγώ ότι δεν λύνεται αναλυτικά.
Μπορούμε να βρούμε πότε ξεκινά η ολίσθηση του κιβωτίου.
Μπορούμε να βρούμε τις απώλειες μέχρι την στιγμή που το μπαλάκι θα βρεθεί στην κατώτερη θέση,
Τα υπόλοιπα είναι δύσκολα.
α, Γιάννη, το ανάποδο, να σταματάει το κιβώτιο πρώτο, αυτό μπορεί, άρα ξαναγράφω την πρώτη μου πρόταση “πολύ δύσκολο το θέμα” και, άρα, μόνο πειραματικά (ή με το διαβολοκόλπο που εσύ ξέρεις) η προσέγγισή του…
Καλησπέρα συνάδελφοι. Δεν ξέρω αν είδατε τη λύση μου, νομίζω ότι μάλλον είναι σωστή. Βλέποντας το Ι.Ρ. του Γιάννη, παρατηρώ ότι όταν το σφαιρίδιο σταματά να ανεβαίνει, έχει την ίδια ταχύτητα με το κιβώτιο! Το θεωρώ λογικό, πρέπει να μην υπάρχει τότε σχετική κίνηση.
Όταν το κιβώτιο σταματά να κινείται, έκανα την υπόθεση ότι η ταχύτητα του σφαιριδίου είναι μηδενική, κάτι που είναι συμβατό με το ότι θα έχουν σχετική ταχύτητα μηδέν, αφού το κιβώτιο έχει ταχύτητα μηδέν, θα έχει τότε και το σφαιρίδιο. Άρα η τάση του νήματος θα είναι ίση με τη συνιστώσα του βάρους του σφαιριδίου Τ=mgσυνθ, κι έτσι η στατική τριβή θα έχει την οριακή της τιμή
Τορ.=μΝ=μ(Μg+Tσυνθ)=>μ[Μg+mg(συνθ)^2]=mgσυνθ.ημθ
για μ=1/4 και M=m υπολογίζω τη γωνία θ με εφθ=2(+-)ριζα(2)=(0,585 ή 2,414). ή (θ=30ο ή θ=73,4ο)
Περίμενα μετά από αυτή τη στιγμή, για κάθε γωνία θ'<θ του νήματος με την κατακόρυφη, να επαληθεύεται ότι Τx<Τορ. Το graph που έκανα για τη σχέση που προκύπτει με αφετηρία το παραπάνω, με διέψευσε!! Για γωνίες που έχουν εφθ'[0, π/50] επαληθεύεται, και όχι για μεγαλύτερες που οι τιμές τους κυμαίνονται από εφθ=π/20 έως εφθ=2,414 ή από εφθ=π/50 έως εφθ=0,585 !
Δεν μπορώ να εξηγήσω την αντίφαση που έχουν οι υπολογισμοί μου με το Ι.Ρ. του Γιάννη. Γιάννη αν θέλεις βάλε τις τιμές που έχω για να δούμε τι γίνεται!!
Επίσης παρατήρησα στο Ι.Ρ. ότι η ολική ενέργεια του συστήματος ,σταθεροποιείται μετά από μερικές αιωρήσεις. Αυτό ενισχύει την πρόβλεψή μου ότι θα γινόταν αυτό κάποια στιγμή, γι’ αυτό και έθεσα στην ομήγυρη τον προβληματισμό μου.
Να είστε καλά .
Καλησπέρα συνάδελφοι.
το πρόβλημα ελύθη!!
Τα ”σκαμπανεβάσματά” μου ως προς τη λογική της αντιμετώπισής μου στον προβληματισμό που έθεσα στην ομήγυρη, οφείλονταν σε ένα αριθμό 3 που είχα παραλείψει στις πολλές πράξεις που έκανα!!!
Μετά από τη διόρθωση, όλα ρέουν ομαλά.
Ολίσθηση του κιβωτίου υπάρχει μέχρι το νήμα να σχηματίσει με την κατακόρυφη γωνία 30ο , και μετά το κιβώτιο δεν ολισθαίνει.
Έτσι οι απώλειες μηχ. ενέργειας λόγω τριβών είναι 86%mgL .
Επομένως σωστή είναι η Γ.
Δείτε την αναλυτική λύση που έκανα, αξίζει τον κόπο.
Ευχαριστώ όσους ασχολήθηκαν με το πρόβλημα που έθεσα στο φόρουμ.
Να είστε καλά.
Σωστή μου φαίνεται Πρόδρομε.