by 
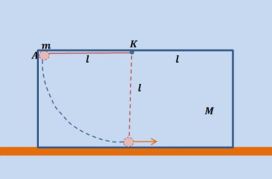
Κενό κιβώτιο μάζας Μ , διαστάσεων l×l×2l βρίσκεται πάνω σε οριζόντιο επίπεδο με το οποίο παρουσιάζει συντελεστή οριακής τριβής μ=0,25. Από το κέντρο Κ της οροφής του, έχουμε δέσει με νήμα , μη εκτατό ,αμελητέας μάζας και μήκους l , σώμα μάζας m=Μ αμελητέων διαστάσεων. Αφήνουμε το σώμα m από τη θέση Α να κινηθεί. Η αντίσταση του αέρα θεωρείται αμελητέα και το κιβώτιο δεν ανατρέπεται.
Η μηχανική ενέργεια που μετατράπηκε σε θερμική λόγω τριβών, είναι ίση με
Α)σχεδόν mgl B) 0,5mgl Γ) 0,86mgl Δ) μηδέν
Ποια σχέση είναι η σωστή;
η απάντησή μου(;)
Είναι σωστή Γιάννη.
Επιβεβαίωσέ το με το Ι.Ρ. θέτοντας τις τιμές που έχω.
Όπως έγραψα και παραπάνω, παράλλειψα ένα 3 στις πράξεις , και το graph έβγαζε μια γραφική παράσταση που ήταν αντίθετη με τη λογική της λύσης μου.
Το “καταραμένο” 3 το έχω στη λύση με κόκκινο χρώμα, για να μου υπενθυμίζει ότι το αμελητέο λάθος δεν το βλέπουμε, γιατί δεν το αμφισβητούμε!!
Ευχαριστώ πολύ για την ενασχόλησή σου.
Η προσομοίωση.
Φαίνεται η αρχική και η τελική ενέργεια.
(160-23)/160=0,856
Ευχαριστώ Γιάννη, να είσαι καλά φίλε. Τώρα έχουμε και οπτικοποίηση του φαινομένου!!
Γιάννη και Πρόδρομε καλησπέρα. Γιάννη αν μπορείς θέλω να δεις κάτι: Δοκίμασε στο ip να αλλάξεις μόνον το μήκος του νήματος, αφήνοντας τα υπόλοιπα στις παλιές τους τιμές (προσπάθησα να το κάνω εγώ και δεν τα κατάφερα, δεν το χειρίζομαι καλά το ip). Είμαι περίεργος να δούμε αν τότε αλλάζει το ποσοστό της απώλειας στην ενέργεια.
Η διασκευή Στάθη:
Μικρότερο νήμα
Από το 80 κάπου στο 11,6. Ίδιο μάλλον ποσοστό.
Καλησπέρα Στάθη. Όπως θα είδες από τη λύση μου, η απώλεια ενέργειας λόγω τριβών είναι 0.86mgL σε αρχική μηχ. Ενέργεια mgL. Άρα το % ποσοστό είναι 86%.
Δεν εξαρτάται από το μήκος L.
Κάτι έχεις στο νου σου!! Δεν μπορώ να το φανταστώ. Μήπως εννοείς τον παράγοντα της γωνιακής ταχύτητας ω του σφαιριδίου; Αλλά από τη λύση μου δεν έχουμε εμπλοκή του! Εννοείται ότι οι διαστάσεις του κιβωτίου είναι τέτοιες που δεν υπάρχει κίνδυνος ανατροπής. Το απέδειξα στην προηγούμενη ανάρτησή μου, αλλά ισχύει κι εδώ.
Πάντως σ’ευχαριστώ για την ενασχόλησή σου με το θέμα.
Να με συγχωρείτε που προχθές δεν συμμετείχα λόγω υποχρεώσεων…, και εκφράσατε τους προβληματισμούς σας χωρίς να μπορώ on line να δώσω διευκρινίσεις.
Να είσαι πάντα καλά.
Πρόδρομε θα μου φανεί πολύ περίεργο αν το αποτέλεσμα δεν εξαρτάται από την αναλογία των μαζών και το μήκος του νήματος (δηλαδή από την συχνότητα των ταλαντώσεων του σφαιριδίου).
Επειδή δεν με εμπιστεύομαι με το ip, κοιτάξτε να δείτε αν το παρακάτω αρχείο ip είναι σωστό. Αν είναι σωστό, τότε μειώνοντας το μήκος στο 1m, η απώλεια γίνεται 42.5%.
Στάθη κόντυνες το νήμα αλλά κράτησες ίδια στάθμη μηδενικής δυναμικής ενέργειας.
Αν αφαιρέσουμε 40 από το αρχικό γίνεται 40. Αφαιρούμε και 40 από το τελικό και γίνεται 6 και κάτι. Οπότε (40-6,2)/40=0,845
Γιάννη το ήξερα ότι κάτι πήγαινε στραβά, η διαφορά ήταν μεγάλη. Υποδιπλασιάζοντας το μήκος του νήματος βρίσκουμε μέσω ip αλλαγές στην ενεργειακή απώλεια, περίπου στο 1%, αν κατάλαβα καλά.
Το διόρθωσα:
Πρόδρομος 4
Μάλλον δεν έχουμε διαφορές στο ποσοστό. Μάλλον κάνουμε προσεγγίσεις στην ανάγνωση και βγαίνουν διαφορούλες. Το πιστεύω πλέον.
Διαισθητικά:
Η κεντρομόλος είναι ανάλογη του υ^2. Το ίδιο και η κινητική ενέργεια.
Βαγγέλη Κουντούρη
Γιάννη Κυριακόπουλε
Γιάννη Μήτση
Στάθη Λεβέτα
και όλοι όσοι παρακολούθησαν τη συζήτηση για το δύσκολο πρόβλημα που έθεσα στο forum,
σας ευχαριστώ!
Να είστε καλά.