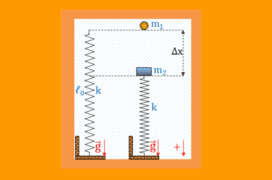
Σώμα μάζας m2 ισορροπεί ακίνητο στο πάνω άκρο κατακόρυφου ιδανικού ελατηρίου σταθεράς k
και φυσικού μήκους l0 , το κάτω άκρο του οποίου έχει στερεωθεί σε ακλόνητο οριζόντιο επίπεδο. Στην
κατακόρυφο που συμπίπτει με τον άξονα του ελατηρίου σε ύψος l0 από το οριζόντιο επίπεδο, συγκρατείται ακίνητο μικρό σφαιρίδιο …
Ελαστική κρούση και απλή αρμονική ταλάντωση
![]()
Καλημέρα Νίκο. Όμορφη! Επειδή δεν προσεξα ότι η εκφώνηση ελεγε για ελαστική κρούση και νόμισα ότι ήταν πλαστική , έκανα λυση για πλαστική κρουση. Δειχνει ενδιαφέρουσα και αυτη η περίπτωση. Για αυτο και την ανεβάζω
Καλησπέρα Γιώργο!
Σε ευχαριστώ για το σχόλιο σου. Μάλιστα έκανες πιο πολύ δουλειά με την πλαστική κρούση! Επιπλέον είτε γίνει ελαστική είτε γίνει πλαστική κρούση, το πλάτος της ταλάντωσης που θα επακολουθήσει ειναι τι ίδιο!
Ναι τα πλάτη είναι ίδια
Και με ενέργειες
Γειά σου Νίκο. Γειά χαρά σε όλους. Ωραίο θέμα . Μια παρατήρηση: Το σώμα m2 μετά την κρούση κάνει επιβραδυνόμενη κίνηση ενώ το άλλο ομαλά επιταχυνόμενη ξεκινώντας με ταχύτητα μηδέν . Δεν θα έπρεπε να ελέγξουμε αν τα σώματα δεν θα ξανασυγκρουστούν πριν να φτάσει το m2 στη κάτω ακραία θέση; Με μια πρόχειρη εξέταση βρίσκω ότι ο χρόνος που χρειάζεται το m1 για να φτάσει στην κάτω ακραία θέση της ΑΑΤ του m2 είναι μικρότερος του Τ/4. Σε κάθε περίπτωση όμως δεν θα έπρεπε να γίνει αυτός ο έλεγχος; Αυτό διορθώνεται εύκολα με τη φράση “αμέσως μετά την κρούση το σώμα m1 απομακρύνεται”. Αυτά αν δεν κάνω κάποιο λάθος.
Συμπληρώνω ότι η αν η κρούση λάβει χώρα μετά τη στιγμή Τ/4 πάλι αλλάζουν τα πράγματα και απαιτείται έλεγχος .
Καλησπέρα Γιώργο!
Δίκαιος ο προβληματισμός σου απλά το ερώτημα αφορά την ταλάντωση του σώματος σαν κίνηση άσχετα με το αν γίνει και δεύτερη κρούση.
Σε ευχαριστώ για τη συμμετοχή!