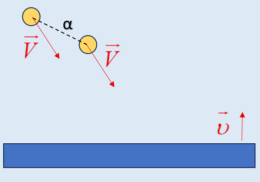
Δυο μπαλάκια κινούνται με ίσες ταχύτητες κατά μέτρο, διεύθυνση και φορά. Ίσα διανύσματα δηλαδή.
Εκτός πεδίου βαρύτητας.
Απέχουν αρχικά απόσταση α.
Μια λεία σανίδα, πολύ μεγάλης μάζας, κινείται όπως στο σχήμα με ταχύτητα κάθετη σ’ αυτήν.
Οι κρούσεις είναι ελαστικές.
Η απόσταση των μπαλακιών τελικά:
- Θα μείνει ίδια. 2. Θα αυξηθεί. 3. Θα μειωθεί.
![]()
Όμορφη Γιάννη.
Δύο πατατηρήσεις
,α) πρέπει να αναφερθεί ότι το x (η οριζόντια απόσταση) παραμενει ίδια λόγω των ίδιων οριζόντιων συνιστωσών της V, Vx
β) η Vx στον κινούμενο παρατηρητήπρεπει να αφαιρεθεί( δεν υπάρχει).
Καλησπέρα Γιώργο.
Υπάρχει η συνιστώσα. Ο παρατηρητής δεν είναι ακίνητος ως προς τη σανίδα.
Τη βλέπει να κινείται προς τα αριστερά.
Έτσι βλέπει τα μπαλάκια να πέφτουν κάθετα στη σανίδα (να μην έχουν οριζόντιες συνιστώσες ταχυτήτων) και λογικά να μένει σταθερή η οριζόντια απόστασή τους.
Ναι το κατάλαβα μετά οτι ο παρατηρητης εκτελει συνθετη κίνηση. Οπότε ακυρες και οι δυο παρατηρήσεις.
Νομίζω Γιάννη ότι η απόσταση θα παραμείνει η ίδια. Δεν ξέρω αν αυτό που λες ότι η ταχύτητα της σανίδας είναι κάθετη σ’ αυτήν παίζει κάποιο ρόλο. Πάντως αν πάρουμε ως σύστημα αναφοράς τη σανίδα, έχουμε δύο μπάλες που πέφτουν πάνω της με ην ίδια ταχύτητα και γωνία, οπότε μετά την ανάκλαση θα απέχουν μεταξύ τους ίδια απόσταση αφού η μεταξύ τους σχετική ταχύτητα θα συνεχίσει να είναι μηδέν
Καλημέρα Πάνο.
Όντως και λοξά να κινείται η σανίδα οι αποστάσεις θα μείνουν ίδιες.
Η σχετική τους ταχύτητα είναι μηδέν εκτός από το χρονικό διάστημα που η μία κατεβαίνει και η άλλη ανεβαίνει.
Πράγματι Γιάννη όταν μετά την ανάκλαση του πρώτου η απόσταση μεταξύ τους αλλάζει. Όταν όμως ανακλαστεί και το δεύτερο, τότε αφού έχουν την ίδια ταχύτητα διανυσματικά, θα αποκτήσουν τελικά την ίδια απόσταση μεταξύ τους η οποία και θα διατηρηθεί αφού η κοινή ταχύτητα θα γίνει μηδέν.
Καλημέρα Πάνο.
Σωστή η παρατήρησή σου.