Δυο μεταλλικά μικρά σφαιρίδια ίδιων διαστάσεων έχουν μάζες m1, m2 όπου m1 = 2m2 και είναι φορτισμένα με ηλεκτρικά φορτία Q1 = +12∙10–6 C, Q2 = –4∙10–6 C αντίστοιχα. Η απόσταση των κέντρων των σφαιριδίων είναι r = 0,3 m και διατηρούνται ακίνητα πάνω στο λείο οριζόντιο επίπεδο με τη βοήθεια αβαρών και μη εκτατών νημάτων όπως φαίνεται στο σχήμα.
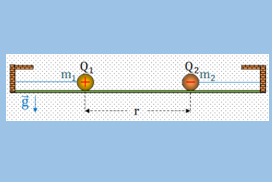
Δίνεται η σταθερά του νόμου Coulomb kc = 9∙109 N∙m2/C2.
Δ1. Να βρεθεί το μέτρο της τάσης των νημάτων.
Κόβουμε συγχρόνως τα νήματα οπότε τα σφαιρίδια με μάζες m1, m2 αρχίζουν να επιταχύνονται και τελικά συγκρούονται κεντρικά και ελαστικά αφού διανύσουν αποστάσεις r1, r2 αντίστοιχα. Να βρεθούν:
Δ2. Οι αποστάσεις r1, r2.
Δ3. Τα ποσοστά % μεταβολής της κινητικής ενέργειας κάθε σφαιριδίου λόγω της κρούσης.
Δ4. Αν γνωρίζουμε ότι μετά την κρούση οι δυνάμεις Coulomb έχουν το μέγιστο δυνατό μέτρο, να βρεθεί το πλήθος των ηλεκτρονίων που μετακινήθηκαν από το σφαιρίδιο μάζας m2 προς το σφαιρίδιο μάζας m1 κατά τη διάρκεια της επαφής τους.
Δίνεται το στοιχειώδες ηλεκτρικό φορτίο e = 1,6∙10–19 C.
Η συνέχεια εδώ.
![]()
Καλημέρα Κυριάκο. Πολύ όμορφη.
Η απάντηση σου στο Δ2 πολύ καλή για τους μαθητές. Με μαθηματικές σχεσεις:
r1= Συ1* Δt
r2= Συ2*Δt= Σ2υ1*Δt=2Συ1*Δt = 2r1
Επίσης στο τελευταίο ερώτημα μπορουμε να χρησιμοποιήσουμε το πόρισμα:
” Όταν το άθροισμα δυο αριθμών είναι σταθερό , το γινόμενο γινεται μεγιστο όταν οι αριθμοί είναι ίσοι” , αρα : q1=q2= 4*10^(-6) C.
Βεβαια εσύ με την λύση σου , στην ουσία, αποδυκνύεις την αλήθεια του πορίσματος.
Καλησπέρα Γιώργο! Το ερώτημα Δ2 ειναι όμορφο αλλά όχι σαν το τελευταίο που κρύβει μέσα του καλά κρυμμένη την Α.Δ.Ε. Η δυναμική ενέργεια αλληλεπίδρασης των σωματιδίων πριν την κρούση είναι αρνητική και μετά γίνεται θετική. Η κινητική ενέργεια του συστήματος δεν μεταβλήθηκε μιας και κρούση είναι ελαστική. Άρα έχουμε μια προφανή αύξηση της ενέργειας του συστήματος! Που βρέθηκε η επιπλέον ενέργεια; Υπάρχει ερμηνεία ή η άσκηση ειναι λάθος;
Τι λέτε συνάδελφοι;
Καλό απόγευμα Νίκο.
Από πού προκύπτει ότι η κινητική ενέργεια του συστήματος, πριν και μετά την κρούση, είναι ίσες; Αυτό προκύπτει από την διατήρηση της ενέργειας, με την υπόθεση ότι η δυναμική ενέργεια παραμένει σταθερή.
Και όταν μιλάμε για δυναμική ενέργεια συμπεριλαμβάνουμε και την ενέργεια λόγω ηλεκτρικής αλληλεπίδρασης;
Αν πάμε τώρα στην δυναμική ενέργεια του συστήματος, πριν την κρούση πόση είναι;
Δεν είναι ϊση με Kq1q2/r, όση υπολογίζουμε θεωρώντας αλληλεπίδραση δύο σημειακών φορτίων, αφού και τα φορτία κάθε σφαιριδίου αλληλεπιδρούν μεταξύ τους και έχουμε άλλους δύο προσθετέους. Έναν που μας δίνει την ενέργεια του ηλεκτρικού πεδίου του ενός σφαιριδίου και έναν του άλλου.
Σε μια τέτοια περίπτωση πρέπει να πάμε στην ενέργεια αγωγού U=1/2 q^2/C, όπου C η χωρητικότητά του, αν γνωρίζουμε ακτίνα σφαιριδίου και να βρούμε την ολική δυναμική ενέργεια του συστήματος.
Το ίδιο θα πρέπει να κάνουμε και μετά την κρούση.
Και η διαφορά τους;
Όταν αντιμετωπίζουμε πρόβλημα σαν αυτό (εκτός κρούσης) μιλάμε για την απώλεια ηλεκτρικής δυναμικής ενέργειας λόγω μεταφοράς φορτίων από τη μια σφαίρα στην άλλη, οπότε παράγεται έργο W=qΔV… το οποίο αποδίδουμε στο φαινόμενο Joule.
Καλησπέρα Διονύση! Οι σφαίρες έχουν ίδιες διαστάσεις, δηλαδή ίδια ακτίνα R σύμφωνα με την εκφώνηση, άρα ίδια χωρητικότητα C που ειναι ανάλογη προς αυτή.
Αν υπολογίσουμε την ενέργεια λόγω κατανομής του ηλεκτρικού φορτίου στους δυο αγωγούς-σημειακά φορτία, με τον τύπο που αναφέρεις, πριν την επαφή και κάνουμε το ίδιο μετά από αυτήν θα διαπιστώσουμε ότι ελαττώνεται και μάλιστα γίνεται η ελάχιστη δυνατή αφού οι διαστάσεις είναι ίδιες και στα δυο σφαιρίδια.
Αν πάλι υπολογίσουμε την αύξηση της δυναμικής ενέργειας αλληλεπίδρασης λόγω της μετακίνησης του ηλεκτρικού φορτίου θα δούμε ότι είναι αντίθετη της μείωσης που υπολογίσαμε από την ανακατανομή των φορτίων στα σφαιρίδια.
Καλησπέρα παιδιά.
Ένα όμοιο θέμα:
Η απάντηση εδώ:
καλησπέρα σε όλους
δεν είδα τις λύσεις και τα σχόλια
η γνώμη μου είναι ότι έπρεπε να δοθεί και η σταθερά G της παγκόσμιας έλξης ή να θεωρηθούν οι βαρυτικές δυνάμεις και ενέργειες ασήμαντες σε σύγκριση με τις αντίστοιχες ηλεκτρικές