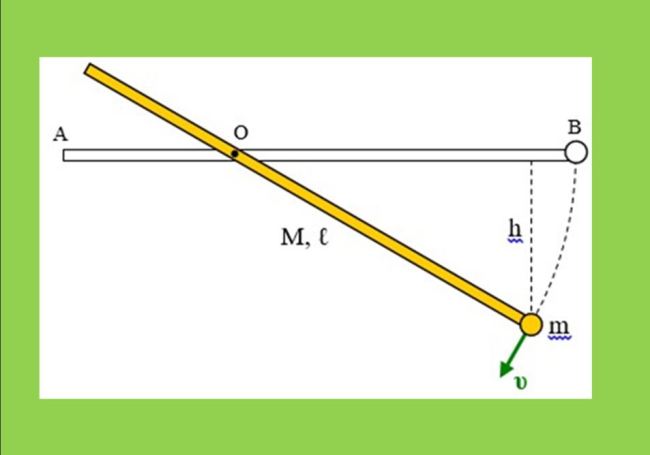
Λεπτή, ισοπαχής, ομογενής ράβδος μάζας Μ και μήκους ℓ μπορεί να στρέφεται χωρίς τριβές γύρω από σταθερό οριζόντιο άξονα Ο, κάθετο σ’ αυτήν, που τη χωρίζει σε δύο τμήματα ΟΑ και ΟΒ. Στο άκρο Β είναι στερεωμένο σφαιρίδιο αμελητέων διαστάσεων, μάζας m.
Το σύστημα ισορροπεί αρχικά με τη ράβδο σε οριζόντια θέση και το αφήνουμε ελεύθερο να κινηθεί.
Να βρεθεί το μέτρο υ της ταχύτητας του σφαιριδίου, όταν αυτό θα έχει κατέλθει κατά ύψος h από την αρχική του θέση.
(Ιράβδου = 1/12·Μ·ℓ² ).
Απάντηση:
Το σφαιρίδιο έπεσε κατά h. Επομένως η δυναμική του ενέργεια μειώθηκε κατά m·g·h και η κινητική του αυξήθηκε κατά:
1/2·m·υ² = m·g·h → υ = (2gh)1/2
Πότε μπορεί να είναι ένα τέτοιο αποτέλεσμα σωστό ;

Δινω και το link αν θελει κανεις να το κατεβασει ή να το δει κάνοντας μεγέθυνση : Ε Δ Ω
![]()
κώστα καλησπέρα
αυτό συμβαίνει όταν η ακτίνα περιστροφής του σημειακού σώματος είναι 2L/3
με κάθε επιφύλαξη
Καλησπέρα Κώστα.
Μια τέτοια λύση ΔΕΝ μπορεί να είναι ποτέ σωστή.
Το αποτέλεσμα, μπορεί να είναι το ίδιο, αν ικανοποιείται κάποια ειδική σχέση όσον αφορά τη θέση του άξονα…
Καλησπέρα Κώστα .
Ύστερα από ένα “κάρο” πράξεις κατέληξα στο αποτέλεσμα του Μανώλη… χ=(ΟΒ)=2L/3.
Σημαίνει άραγε κάτι ; …σκέφτομαι :()
Γειά σου Διονύση.
Εννοείς ότι η λύση του Κώστα δεν μπορεί να δοθεί σαν λύση … σαφές αυτό.
”Το σφαιρίδιο έπεσε κατά h. Επομένως η δυναμική του ενέργεια μειώθηκε κατά m·g·h και η κινητική του αυξήθηκε κατά:
1/2·m·υ² = m·g·h → υ = (2gh)1/2
Πότε μπορεί να είναι ένα τέτοιο αποτέλεσμα σωστό ;”
φυσικά σε μια τέτοια λύση το μόνο που είναι σωστο είναι το αποτέλεσμα, τίποτε άλλο
Καλησπέρα Παντελή.
Αυτό ακριβώς εννοώ. Δεν είναι αυτή η λύση, ούτε μπορεί να γίνει αποδεκτή ως λύση.
Ότι το αποτέλεσμα σε κάποια ειδική περίπτωση, μπορεί να είναι αυτό, ναι αυτό μπορεί να συμβεί (προφανώς δεν έκανα πράξεις, αλλά το μήκος που δίνετε ο Μανόλης και συ, έχει …τα προσόντα 🙂 ).
Να δώσω και μια άλλη εκδοχή.
Αν η ράβδος έχει αμελητέα μάζα.
Αυτό που λέμε… αβαρής!
Καλησπέρα Διονύσης.
Κλέβεις 🙂
Αν υπάρχουν και άλλες συντηρητικές δυνάμεις, εκτός του βάρους, θα έπρεπε να υπάρχουν και οι προσθετέοι με τις υπόλοιπες δυναμικές ενέργειες…
Διονύση με κρέμασες!!!
Απάντησα σε σχόλιο που…σκέφτεσαι να βάλεις 🙂
Καλησπέρα σε όλους,
Εμένα μου φαίνεται σωστή!
«Αν ένα σώμα ανταλλάσσει ενέργεια με το περιβάλλον του μέσω συντηρητικών δυνάμεων, τότε η μηχανική του ενέργεια παραμένει σταθερή»!
Οπότε: ½mυ²=mgh → … 🙂 🙂
Παιδιά συγγνώμη,
Πήγα να διορθώσω το σχόλιό μου και προλάβατε και γράψατε από κάτω!
θα ήθελα να προσθέσω επίσης ότι αν τη στιγμή που ξεκινα το σημειακό , η δύναμη που δέχεται απο τη ράβδο είναι μηδεν τότε στη συνέχεια η δύναμη που θα του ασκεί η ράβδος δεν εχει εργο
Έχεις δίκιο Διονύση, πήγα να διορθώσω τα Times New Roman και πήγε πιο κάτω το σχόλιο. Δεν ξέρω αν μπορείς να το μεταφέρεις πιο πάνω.
Για τις δυνάμεις που γράφεις … η μόνη συντηρητική που βλέπω στο σφαιρίδιο είναι το βάρος του 🙂
Γεια σου και πάλι Διονύση.
Ας το πούμε τότε αλλιώς.
Αν δεν εξασφαλίσεις ότι η δύναμη που δέχεται το σφαιρίδιο από τη ράβδο, δεν παράγει έργο, δεν μπορείς να διατυπώσεις καμιά ΑΔΜΕ…
Μανώλη εννοείς ότι το σφαιρίδιο δεν δέχεται δύναμη από τη ράβδο καθώς κατέρχεται 🙂