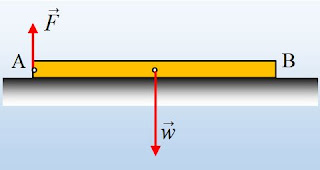
Σε λείο οριζόντιο επίπεδο ηρεμεί μια ομογενής δοκός ΑΒ μήκους 2m και μάζας 24kg. Σε μια στιγμή στο άκρο Α τη δοκού, ασκούμε μια κατακόρυφη δύναμη, με φορά προς τα πάνω, μέτρου F=90Ν και παρατηρούμε ότι η σανίδα συνεχίζει να ηρεμεί.
- Να βρεθεί η δύναμη που ασκεί το επίπεδο στη δοκό, καθώς και η ροπή της ως προς το κέντρο μάζας Κ της δοκού.
- Ποια η μέγιστη τιμή F1 που μπορεί να πάρει το μέτρο της δύναμης, χωρίς να πάψει η δοκός να ισορροπεί;
- Αν η δύναμη πάρει τιμή F2 =200Ν, να βρεθεί η αρχική επιτάχυνση που θα αποκτήσει το άκρο Α της δοκού.
- Υποστηρίζεται η θέση ότι αυξάνοντας το μέτρο της ασκούμενης κατακόρυφης δύναμης F, στο ένα άκρο της δοκού, μπορούμε να πετύχουμε, το άμεσο χάσιμο της επαφή της ράβδου με το επίπεδο. Να εξετάσετε αν αυτό μπορεί να συμβεί.
Δίνεται η ροπή αδράνειας μιας ομογενούς δοκού ως προς άξονα κάθετο που περνά από το μέσον της Ιcm= Μℓ2/12 και g=10m/s2.
ή
![]()
Άριστη!
Θα συνεχίσεις με το “σε ποια θέση ανασηκώνεται”;
Καλημέρα Διονύση ,καλημέρα Γιάννη.
Ένας μήνας με καθημερινές απουσίες πάει πολύ, αλλά κοινωνικές υποχρεώσεις
με πέταξαν στη νήσο , προστέθηκαν κι άλλα τινά όπως ο “Πυθαγόρας” στην …ατζέντα της εγγονής ,ήρθε κι ο πόλεμος που έκαμε θρύψαλα τη λογική μου και είπα σήμερα να δώσω σημεία “ζωής” .
Με μια ράβδο και τη δράση μιας δύναμης , έφτιαξες ωραία ερωτήματα “σκαλοπάτια” σκέψης, με όμορφο πλατύσκαλο το iii) !
Να έχεις πάντα όμορφες ιδέες, στοχεύοντας σε συγκεκριμένα κέντρα.
πολύ καλή, Διονύση
(στην πρώτη σειρά της απάντησης άλλαξε αμοιβαία τα σύμβολα F και Ν)
Καλό μεσημέρι παιδιά.
Γιάννη, Παντελή και Βαγγέλη, σας ευχαριστώ για το σχολιασμό.
Παντελή… περιμένουμε!
Γειά σου Διονύση. Πολύ μου άρεσε.
Καλό απόγευμα Αποστόλη.
Σε ευχαριστώ.
Διονύση για μια ακόμη φορά το πας παραπέρα. Άλλη μια καινούρια ιδέα και αυτό από μόνο του έχει την αξία του. Μπράβο!
Μόνο που σκέφτομαι, αλλά σίγουρα δεν έχω χρόνο να το δω, μήπως πρέπει η άσκηση της Ν να γίνεται με μια γραμμική κατανομή σε όλο το μήκος της ράβδου και βέβαια συνισταμένη αυτή που υπολογίζεις, όπως φαντάζομαι ότι γίνεται πριν ασκηθεί η F.
Καλησπέρα Στέφανε και σε ευχαριστώ για το σχολιασμό.
Προφανώς η κάθετη δύναμη στήριξης δεν ασκείται σε ένα σημείο, αλλά σε όλη την επιφάνεια που έρχεται σε επαφή με το έδαφος.
Αλλά αυτή η κατανομή μπορεί να προσεγγιστεί με μια δύναμη (συνισταμένη) και μια ροπή ως προς το μέσον της σανίδας.
Πώς μπορεί να εκφραστεί η ροπή αυτή; Θεωρώντας μία δύναμη με μεταφορά του φορέα της!
Έτσι δεν μελετάμε κάθε περίπτωση ανατροπής ενός στερεού, όπως για παράδειγμα:
Ο ελάχιστος χρόνος
Καλησπέρα Διονύση
Πολύ ωραία παρουσίαση. Εξαιρετικό το Ερώτημα 4.
Διονύση με καλύπτεις. Σε ευχαριστώ.
Να είσαι καλά.
Καλό βράδυ
Καλημέρα Μανώλη, σε ευχαριστώ για το σχολιασμό και χαίρομαι που σου άρεσε.
Καλημέρα
Με αφορμή και το σχόλιο του Γιάννη βρήκα, με κάποια ταλαιπωρία, τη σχέση που συνδέει το Ν με με τη γωνία στροφής της ράδου θ για F>mg/2. Το θέμα μου φαίνεται πολύ ενδιαγέρον και όταν το ολακληρώσω θα δώσω το σύνδεσμο που θα οδηγεί στο σχετικό docx αρχείο. Στην εικόνα δίνω μια σύνοψη
.
θ=47,47 μοίρες
Καλημέρα Μανώλη.
Σε ευχαριστώ για την μελέτη που μας δίνεις.
Καλημέρα
Τελικά ολοκλήρωσα τη διερεύνηση του θέματος. Στο διάγραμμα φαίνεται ότι όσο μεγάλου μέτρου και αν είναι η εεξασκούμενη δύναμη η ράβδος θα συρθεί στο δάπεδο πριν απογειωθεί