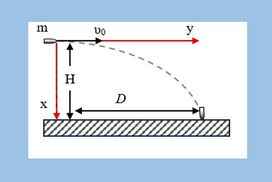
Από ύψος Η πάνω από το έδαφος εκτοξεύεται οριζόντια μία σφαίρα μάζας m=0,5Kg με ταχύτητα μέτρου υ0=20m/s. Το βλήμα φτάνει στο έδαφος τη στιγμή t=4s και έχει ταχύτητα μέτρου υ=30m/s και κατεύθυνση κατακόρυφη. Σε όλη τη διάρκεια της κίνησης το βλήμα δέχεται σταθερή δύναμη F μέτρου F. Θεωρώντας την κίνηση σύνθετη στους άξονες x και y να απαντήσετε στα ακόλουθα ερωτήματα.
i) Να βρείτε την επιτάχυνση της σφαίρας.
ii) Να υπολογίσετε τη δύναμη F.
iii) Nα βρείτε τη μετατόπιση της σφαίρας σε όλη τη διάρκεια της κίνησής της.
iv) Να υπολογίσετε το έργο της δύναμης F σε όλο το διάστημα της κίνησης.
v) Βρείτε την ισχύ της δύναμης F τη χρονική στιγμή t=2s.
Δίνεται το μέτρο της επιτάχυνσης της βαρύτητας g=10m/s2.
Απάντηση
![]()
Χρήστο πολύ ενδιαφέρουσα η ιδέα σου.
Αξίζει ίσως να αναφερθεί πως στο ίδιο αποτέλεσμα (κάθετη ταχύτητα στο έδαφος)
φθάνουμε με διαφορετικές δυνάμεις, ανάλογα τί επιθυμούμε ή τί μπορούμε….
Καλή δύναμη στη νέα σχολική χρονιά
Καλημέρα Χρήστο.
Πολύ καλή ιδέα. Αν έδινες τελική κατακόρυφη ταχύτητα 20m/s, μήπως είχες καλύτερα αποτελέσματα;
Καλημέρα Χρήστο και λοιποί “συνδαιτυμόνες”!
Ενδιαφέρον το οριζόντιο φρενάρισμα, για πρόσπτωση με ταχύτητα κατακόρυφη καθώς και τα ερωτήματα που έθεσες!
Αν το βλήμα το σχεδίαζες σαν σφαίρα δεν θα έκανα την επόμενη παρατήρηση.
Το βλήμα στο σχήμα σου πως πέφτει με τον άξονα του κατακόρυφο ,ποιά ροπή το έστρεψε;
Νομίζω … πρέπει να σχεδιαστεί όπως τη στιγμή της βολής.
Δεν σου κρύβω πως χρόνια πριν με απασχόλησε το …πως το ακόντιο των ακοντιστών ενώ φεύγει με “θετική κλίση” πέφτει στο έδαφος με “αρνητική”; Βέβαια ορισμένες πτήσεις δεν τα καταφέρνουν.
Αν καλά και με όποια ερωτηματικά, για άλλους παράγοντες, έχω καταλάβει ,ο ρίπτης προσδίδει κατά την εκτίναξη του ακοντίου κατάλληλη “εμπειρική” ω για περιστροφή και πτώση με τη μύτη.
Καλή σχολική χρονιά εύχομαι
Καλησπέρα σε όλους.
Θοδωρή, Διονύση και Παντελή ευχαριστώ για το σχόλιο.
Θοδωρή έχεις δίκιο μπορεί να προέλθει με διάφορους τρόπους. Δεν ξέρω πως μπορεί να γραφεί για να καταλάβει κάποιος ότι εννοώ μια τέτοια δύναμη…
Διονύση έχεις δίκιο. Το είχα στην αρχή σε τέτοια εκδοχή και μάλιστα εβγαινε και αχ=αy και απο εκεί να ξεκλειδώνει η άσκηση αλλά ήταν πιο δύσκολη η εκδοχή και την άφησα αλλά άλλαξα και τα νούμερα.
Παντελή έχεις απόλυτο δίκιο. Για να τονιστεί η κατακόρυφη ταχύτητα στράφηκε η σφαίρα αλλά δεν είναι σωστό. Η διόρθωση στο σχήμα έγινε. Μάλιστα αν θυμάσαι υπάρχει τετοιο ερώτημα στο S4E.
Παντελή ψαρεύοντας στο διαδίκτυο βρήκα αρκετά για το ακόντιο.
Περισσότερα
paper
simulation
Σύνδεσμος
Καλησπέρα Χρήστο. Καλή σχολική χρονιά.
Ωραία άσκηση, για καλούς μαθητές. Δεν πρόσεξα ότι η δύναμη είναι τυχαίας διεύθυνσης και την έλυσα με οριζόντια προς τα αριστερά. Ίσως πρέπει να δίνεται στo σχήμα το διάνυσμα F. Όσο το μάθημα είναι 2ωρο δεν προλαβαίνουμε να κάνουμε τέτοιες καλές ασκήσεις, για να δείξουμε στους μαθητές μας πως εφαρμόζουμε την ΑΑΚ. Έκανα 4 μαθήματα στην οριζόντια βολή και τώρα μένουν άλλα 4 για την κυκλική κίνηση. Προηγούνται όμως εκλογές, περίπατος και ημέρα αθλητισμού. 😆
Και όλα τα τμήματα έχουν μέσα 27 με τους μισούς για Οικονομικά…
Χρήστο ευχαριστώ για τα link ,όμως το paper δεν ανοίγει.
Αντρέα καλησπέρα.
¨Εχεις δίκιο η άσκηση δεν είναι εύκολη και είναι για απαιτητικούς μαθητές. Όσο για την δύναμη αν δεν υπάρχει η κατακόρυφη συνιστώσα η ταχύτητα υy θα είχε μέτρο 40m/s. ¨Ετσι σαν βοηθητικό στοιχείο για να μην σχεδιαστει η δύναμη θα ήταν να εξετάσετε αν υπάρχει συνιστώσα στην κατακόρυφη διεύθυνση.
Τώρα γι αυτά που περιγράφεις νομίζω δεν χρειάζεται καν σχόλιο. Η αλήθεια είναι ότι έχω το προνόμιο το τμήμα να είναι ομοιογενές και οι μαθητές να ενδιαφέρονται για το κάτι παραπάνω.
Παντελή ο σύνδεσμος διορθώθηκε.