Το σώμα του σχήματος, αμελητέων διαστάσεων, ταλαντώνεται σε λείο οριζόντιο επίπεδο, δεμένο στο άκρο ιδανικού ελατηρίου και τη στιγμή t1 περνά από την θέση Β, με ταχύτητα υ1 με κατεύθυνση προς τα δεξιά. Στο σώμα ασκείται δύναμη απόσβεσης Fαπ=-bυ και η κίνηση μπορεί να είναι φθίνουσα ή και εξαναγκασμένη, αφού μπορεί να ασκείται στο σώμα και εξωτερική αρμονική δύναμη.
i) Η θέση ισορροπίας, από την οποία μετράμε και την απομάκρυνση x, είναι η θέση Ο, όπου το ελατήριο έχει το φυσικό μήκος του:
Α) Μόνο για την περίπτωση της φθίνουσας ταλάντωσης.
Β) Μόνο για την εξαναγκασμένη ταλάντωση.
Γ) Και στις δύο ταλαντώσεις.
Δ) Σε καμιά από τις δύο αυτές ταλαντώσεις.
ii) Αν η ταλάντωση είναι φθίνουσα:
Α) Η επιτάχυνση του σώματος στη θέση Β, όπου η απομάκρυνση είναι x1, έχει μέτρο:
α) α1< k|x1|/m, β) α1= k|x1|/m, γ) α1> k|x1|/m.
Β) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Γ) Το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια ταλάντωσης Ε3 και επιτάχυνση μέτρου α3.
Γ1) Αν η ενέργεια ταλάντωσης την στιγμή t1 είναι ίση με Ε1, τότε:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Γ2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
iii) Αν η ταλάντωση του σώματος είναι εξαναγκασμένη και η απομάκρυνση του σώματος ικανοποιεί την εξίσωση x=Α∙ημ(ωδt):
Α) Η επιτάχυνση του σώματος στη θέση Ο είναι μηδενική ή όχι;
Β) Αν το σώμα τη στιγμή t1 έχει επιτάχυνση α1 και ενέργεια ταλάντωσης Ε1, τότε όταν το σώμα θα ξαναπεράσει από την θέση Β κινούμενο προς τα δεξιά, μια επόμενη χρονική στιγμή t3, έχοντας ενέργεια Ε3 και επιτάχυνση μέτρου α3, θα ισχύουν:
Β1) Για τις ενέργειες ταλάντωσης:
α) Ε3 < Ε1, β) Ε3 = Ε1, γ) Ε3 > Ε1.
Β2) Για τα μέτρα των επιταχύνσεων α1 και α3 ισχύει:
α) α3 < α1, β) α3 = α1, γ) α3 > α1.
Να δικαιολογήσετε τις απαντήσεις σας.
ή
![]() Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
![]() Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
Η φθίνουσα σε αντιπαράθεση με την εξαναγκασμένη
![]()
Αφιερωμένη στον Χρήστο Αγριόδημα, ο οποίος την … προκάλεσε!
Διονύση καλημέρα
Βάζεις πολλά πράγματα στη θέση τους.
Εγώ προσωπικά τακτοποίησα αυτά τα οποία τελούσαν υπό διευκρίνιση η επαλήθευση και σε ευχαριστω.Ειναι ένα κείμενο που ενδιαφέρει ( το λέω μετα λόγου γνώσεως)
πολλούς συναδέλφους.
Καλημέρα Παρμενίων και σε ευχαριστώ πολύ για το σχόλιο.
Αντί να ακολουθήσω την “κλασσική” μέθοδο, μιλώντας για το πόσο είναι η δυναμική ενέργεια στην εξαναγκασμένη και αν αυτή δίνεται από τη μια ή την άλλη εξίσωση και τι συμβαίνει στο συντονισμό, και, τι αν η ιδιοσυχνότητα είναι μικρότερη ή μεγαλύτερη από την συχνότητα του διεγέρτη, πράγματα που έχουν διατυπωθεί πολλές φορές, είπα να δούμε τα πράγματα από άλλη οπτική γωνία…
Ελπίζω να φανεί χρήσιμη σε συναδέλφους και μαθητές…
ΥΓ
Να τονίσω ότι πρέπει να “διαβάζεται” και να μην περνά απαρατήρητη η εξίσωση:
1/2 kx^2…
Εξίσωση η οποία περιέχει τη σταθερά του ελατηρίου και όχι κάποια σταθερά που να συνδέεται με την συχνότητα του διεγέρτη.
Διονύση για άλλη μια φορά ρίχνεις φως σε κάτι που το βιβλίο όχι μόνο το έχει στο σκοτάδι αλλά ούτε καν αναφέρει κάτι
Πολύ καλή και αναλυτική εφαρμογή
Καλημέρα κύριε Διονύση.θα ήθελα να καταλάβω πως η θ.Ι. ταυτίζεται με τη θέση φυσικού μήκους αν στη θέση αυτή δεν ισχύει ότι ΣF=0, είτε στην περίπτωση της φθίνουσας ταλάντωσης είτε στην περίπτωση της εξαναγκασμενης ταλάντωσης.Ιδίως στην περίπτωση των εξαναγκασμένων ταλαντώσεων δεν θα υπάρχει διαφοροποίηση αν έχουμε συντονισμό ή όχι;Στην περίπτωση του συντονισμού όντως ΣF = Fελ. αφού οι δυνάμεις απόσβεσης και διεγέρτη είναι αντίθετες.
Καλημέρα Κώστα, καλημέρα Παύλο.
Σας ευχαριστώ για το σχολιασμό.
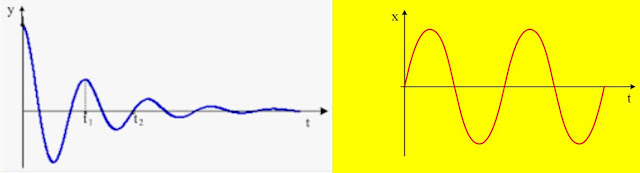
Παύλο, ας δούμε στο σχήμα, όπου αριστερά είναι η γραφική παράσταση x=f(t) για την φθίνουσα και δεξιά για μια εξαναγκασμένη, μετά το πέρας των μεταβατικών φαινομένων:
Στην φθίνουσα τι είναι αυτό το x; Απομάκρυνση από ποια θέση; Για δες, πού καταλήγει η καμπύλη; Πού, σε ποια θέση τελικά το σώμα ισορροπεί; Δεν ισορροπεί (και σταματά…) στη θέση x=0; Και μόλις σταματήσει, δέχεται κάποια οριζόντια δύναμη; Προφανώς όχι. Αλλά τότε αυτή η θέση είναι η θέση φυσικού μήκους του ελατηρίου.
Πάμε στην εξαναγκασμένη. Υπάρχει κάποια αμφιβολία ότι όταν x=0 θα έχουμε και α=0; Αυτό προκύπτει από τις αντίστοιχες χρονοεξισώσεις, για ΚΑΘΕ κυκλική συχνότητα του διεγέρτη. Δεν μας ενδιαφέρει αν έχουμε ή όχι συντονισμό.
Και τότε ποιες δυνάμεις ασκούνται στο σώμα στη θέση x=0;
Οι δυνάμεις (οριζόντιες) είναι δύο, η δύναμη απόσβεσης (με μέγιστο μέτρο) και η δύναμη του διεγέρτη, όπου αυτές είναι αντίθετες, αφού α=0.
Αυτό δείχνει συντονισμό; Όχι. Οι δυο δυνάμεις στη θέση x=0 είναι αντίθετες, χωρίς να σημαίνει ότι αυτό ισχύει σε κάθε θέση. Στο συντονισμό οι δυο δυνάμεις είναι πάντα αντίθετες σε κάθε θέση.
Είναι άριστη!
Γειά σου μάστορα Διονύση!
Απίθανη από τις καλύτερες ever
Έχετε απόλυτο δίκιο ότι τελικά το σώμα ακινητοποιείται στη θέση φυσικού μήκους του ελατηρίου αλλά τα διαγράμματα δεν μας δειχνουν ποιά ειναι η θ.ι δηλαδή αν είναι η θέση φυσικού μήκους ή όχι αλλά το πότε διέρχεται από τη θέση αυτή. Στη περίπτωση των δύο αυτών κινήσεων η θέση για την οποία ισχύει ΣF =0 νομίζω μεταβάλλεται .
Καλησπέρα σε όλους.
Γιάννη, Αποστόλη και Μανόλη, σας ευχαριστώ για το σχόλιο.
Να είσαστε καλά.
Παύλο δεν καταλαβαίνω, πού εστιάζεται η διαφωνία.
Θα μου επιτρέψεις να δώσω δύο εικόνες από δύο προσομοιώσεις.
Η πρώτη για την φθίνουσα ταλάντωση.
Το σώμα βρίσκεται τη στιγμή t=0 στη θέση x=0, με το ελατήριο στο φυσικό μήκος του και αποκτά αρχική ταχύτητα προς τα δεξιά.
Η απομάκρυνσή του από την θέση x=0 (ΘΦΜ) φαίνεται στην εικόνα.
Αμφισβητείς ότι γύρω από αυτήν την θέση πραγματοποιείται η ταλάντωση;
Το αρχείο i.p. φθίνουσα ταλάντωση.
Το 2ο αρχείο είναι για την εξαναγκασμένη.
Το σώμα ηρεμεί στο άκρο του ελατηρίου, το οποίο έχει το φυσικό μήκος του (Lo=4m) στη θέση x=0. Δέχεται την επίδραση οριζόντιας αρμονικής δύναμης και στο διάγραμμα φαίνεται η θέση του, σε συνάρτηση με το χρόνο
Είναι φανερά και τα μεταβατικά φαινόμενα και η συνέχεια.
Δεν είναι φανερό ότι η ταλάντωση πραγματοποιείται γύρω από την ΘΦΜ (x=0);
Το αρχείο i.p. εξαναγκασμένη ταλάντωση
Δεν διαφωνώ ότι η θέση φυσικού μήκους είναι η x=0 αλλά ότι είναι η θέση ισορροπίας. Το χ=0 δεν σημαίνει ΣF=0 .
Αν την θέση αυτή θέλεις Παύλο να την ονομάσεις “θέση άνω κάτω Ραχούλας” κάντο.
Δεν αλλάζει τίποτα.
Το θέμα έχει συζητηθεί, στο παρελθόν, υπήρχαν συνάδελφοι που υποστήριζαν ότι αφού στη φθίνουσα (μόνο στη φθίνουσα…) στη θέση x=0 η συνισταμένη δεν είναι μηδενική, δεν δικαιούται να ονομάζεται “θέση ισορροπίας“, άποψη που προσωπικά έχω απορρίψει.
Αυτό σημαίνει ότι συνεχίζω να την αποκαλώ “θέση ισορροπίας” παρότι τονίζω ότι στην φθίνουσα η συνισταμένη δεν είναι μηδενική, σε κάθε πέρασμα του σώματος από την θέση αυτή. Η συνισταμένη είναι μηδενική αν αφεθεί το σώμα εκεί, με αποτέλεσμα να παραμείνει ακίνητο, όπως θα ισορροπήσει επίσης εκεί, μόλις χάσει όλη την ενέργεια και πάψει η ταλάντωση.
Όσον αφορά την εξαναγκασμένη στην οποία είχες εκφράσει επίσης διαφωνία, σε αυτήν ισχύει ότι στην θέση x=0 ισχύει και η συνθήκη ΣF=0…