
Το επίπεδο είναι λείο και οριζόντιο. Το μπαλάκι είναι δεμένο με ιδανικό νήμα το οποίο έχει περάσει από τρύπα του επιπέδου.
Έχει μάζα 0,1 kg.
Το οριζόντιο τμήμα έχει αρχικά μήκος 2 m και το μπαλάκι ταχύτητα 1 m/s, κάθετη στο νήμα.
Κάποια χρονική στιγμή που την εκλαμβάνουμε ως στιγμή μηδέν αρχίζουμε να τραβάμε το νήμα με σταθερή ταχύτητα 0,5 m/s.
Να υπολογιστεί η ταχύτητα του μπαλακιού συναρτήσει του χρόνου, η τάση του νήματος συναρτήσει του χρόνου και το έργο της από την στιγμή μηδέν ως την στιγμή 2 s.
![]()
Όμορφη Γιάννη! Στο διάγραμμα μήπως οι ταχύτητες της υ έχουν άλλες τιμές σύμφωνα με τον ατιστοιχο τύπο;
Ευχαριστώ Γιώργο.
Έκανα διόρθωση. Είχα πληκτρολογήσει άλλη σχέση.
Καλησπέρα Γιάννη, κάτι που με προβληματίζει και δεν κατανοώ
Σύμφωνα με τη σχέση που βγάζεις για την τάση, τη στιγμή t=0
η τάση έχει μέτρο Τ=0,05Ν
Αυτή όμως είναι η απαραίτητη κεντρομόλος δύναμη για l=2m και υο=1m/s
Με αρχικές συνθήκες Τ=0,05Ν και ταχύτητα κάθετη στο νήμα, δεν καταλαβαίνω
γιατί η τροχιά δεν παραμένει κυκλική….
Στη δική μου λογική για να αρχίσει να μειώνεται το μήκος του νήματος στο τραπέζι,
εφόσον η αρχική ταχύτητα είναι κάθετη στο νήμα, πρέπει η τάση να είναι μεγαλύτερη
από την απαιτούμενη κεντρομόλο
Μάλλον βλέπεις κάτι, που εγώ δεν βλέπω….
Γεια σου Θοδωρή.
Σκέφτομαι ότι η τροχιά δεν παραμένει κυκλική διοτι κάθε στιγμή το κέντρο είναι άλλο.
Προβληματισμό στον υπολογισμό είχε και ο Χρήστος.
Δεν αποκλείω να έχω κάνει λάθος.
Μάλλον είναι σωστό:

Με μάζα 0,1 kg και την εικονιζόμενη επιτάχυνση, η δύναμη είναι 0,05 Ν.
Καλημέρα σε όλους.
Γιάννη, όμορφη άσκηση.
Μία ακόμη λύση,
στον σύνδεσμο εδώ.
Καλό Σαββατοκύριακο!
Καλημέρα Γιάννη, καλημέρα σε όλους και καλό ΣΚ.
Γιάννη, μια άσκηση (ουσιαστικά) μας έμεινε στην ύλη στην ΑΔΣ, ας την μελετήσουμε!!! Ωραία η παραπάνω μελέτη, έχω και γω μια έτοιμη, σε λίγες μέρες…
Θοδωρή, η άσκηση ξεκινά με την υπόθεση ότι το σώμα έχει μια σταθερή ταχύτητα στην διεύθυνση της ακτίνας. Και για αυτή την σταθερή ταχύτητα, δεν χρειάζεται κάποια δύναμη για την “διατήρησή” της.
Έτσι το μόνο που απομένει είναι η ανάγκη μιας δύναμης που να μεταβάλλει την άλλη ταχύτητα, την εφαπτομενική και αυτή είναι η κεντρομόλος.
Δεν έχουμε δηλαδή μια ομαλή κυκλική κίνηση με ορισμένη ταχύτητα και μια αρχική τάση, όπου κάποια στιγμή αυξάνουμε την δύναμη που ασκούμε στο άκρο του νήματος (και άρα την τάση), με αποτέλεσμα να αποκτήσει και συνιστώσα επιτάχυνση ακτινική, έτσι ώστε να αρχίσει να αποκτά και συνιστώσα ακτινική ταχύτητα.
Καλημέρα Θρασύβουλε.
Ευχαριστώ.
Πολυ κομψή λύση:
Καλημέρα Διονύση.
Ευχαριστώ.
Αυτή ήταν και η δική μου σκέψη, η μηδενική ακτινική επιτάχυνση.
Από τη δυναμική του στερεού μερικές τέτοιες ασκήσεις έμειναν τελικά.
Καλό απόγευμα σε όλους
Διονύση, γράφεις:
“”η άσκηση ξεκινά με την υπόθεση ότι το σώμα έχει μια σταθερή ταχύτητα στην διεύθυνση της ακτίνας. Και για αυτή την σταθερή ταχύτητα, δεν χρειάζεται κάποια δύναμη για την “διατήρησή” της.”
Νομίζω πως αυτό δεν προκύπτει από την εκφώνηση.
Γράφει ο Γιάννης:
“Κάποια χρονική στιγμή που την εκλαμβάνουμε ως στιγμή μηδέν αρχίζουμε να τραβάμε το νήμα με σταθερή ταχύτητα 0,5 m/s.”
Τι σημαίνει αρχίζουμε;
Το μπαλάκι εκτελούσε ΟΚΚ ακτίνας 2m με ταχύτητα 1m/s και κάποια στιγμή
αυξήσαμε τη δύναμη ώστε να αποκτήσει ακτινική ταχύτητα 0,5 m/s, την οποία
καταργώντας την “επιπλέον” δύναμη διατηρεί στη συνέχεια…
Αυτό κατά τη γνώμη μου, ενισχύεται και από τη λύση
Γράφει σωστά ο Γιάννης, “αναλύουμε την ταχύτητα”….
Αυτό σημαίνει πως η ταχύτητα δεν ήταν η “κάθετη στο νήμα” ταχύτητα 1m/s
Όμως η εκφώνηση γράφει “το μπαλάκι έχει ταχύτητα 1m/s κάθετη στο νήμα”
Μάλλον ο Γιάννης αναφέρεται στη συνιστώσα της ταχύτητας
Γιάννη, η άσκηση είναι πανέξυπνη, αλλά προσωπικά θα έδινα άλλη εκφώνηση
Καλησπέρα Θοδωρή.
Η διατύπωση του Γιάννη, είναι αυτό που λέμε “ένα σώμα είναι ακίνητο και κάποια στιγμή αποκτά ταχύτητα υ=2m/s κινούμενο ευθύγραμμα ομαλά”.
Γίνεται αυτό και τι εννοούμε λέγοντάς το;
Εννοούμε ότι για απειροελάχιστο χρόνο ασκείται στο σώμα μια κατάλληλη δύναμη, του προσδίδει επιτάχυνση και μόλις η ταχύτητά του γίνει ίση με 2, παύει να ασκείται. Φαντάσου μια κρούση…
Και εδώ ο Γιάννης δεν μελετά πώς μπορεί να αποκτηθεί αυτή η ακτινική ταχύτητα, θεωρώντας την ότι αποκτάται ακαριαία και… πάμε παρακάτω.
Καλησπέρα και πάλι, διαφωνώ Διονύση.
Στην κρούση, το αίτιο είναι ορατό. Η διδακτική ασάφεια στην εκφώνηση,
καθορίζεται από την τάξη στην οποία απευθυνόμαστε….
Στην κινηματική της Α’ Λυκείου, όπου ακόμα ο 2ος ΝΝ είναι άγνωστος,
μία τέτοια ασάφεια δικαιολογείται… Στη Γ’ Λυκείου καλό θα ήταν όταν
μπορούμε να την αποφεύγουμε…
Προσωπικά θα έγραφα:
“Το μπαλάκι κινείται σε λείο οριζόντιο επίπεδο και κάποια στιγμή που θεωρούμε ως to=0, έχει ταχύτητα υ η οποία αναλύεται σε δύο κάθετες συνιστώσες: μία κάθετη στο νήμα u μέτρου 1 m/s και μία στη διεύθυνση του νήματος v μέτρου 0,5 m/s. Την ίδια στιγμή το οριζόντιο τμήμα του νήματος έχει μήκος 2m.
Στο μπαλάκι ασκoύμε μέσω του νήματος κατάλληλη δύναμη, η οποία μεταβάλλει το
μήκος του οριζόντιου νήματος, αλλά όχι το μέτρο της συνιστώσας της ταχύτητας στη διεύθυνση του νήματος. Υπολογίστε…..”
Γνωρίζω ότι ο Γιάννης διαφωνεί με τις εκτενείς εκφωνήσεις, αλλά κατά τη γνώμη μου,
σε αχαρτογράφητα νερά και σε επίπεδο Γ’ Λυκείου είναι απαραίτητες….
Καλησπέρα παιδιά.
Ο Θοδωρής δεν έχει άδικο. Μια ασυνέχεια την στιγμή μηδέν είναι προβληματική κατάσταση.
Γιάννη καλησπέρα.
Ωραία η προέκταση που δίνεις. Θα πρόσθετα ότι η μεταβολή γίνεται πολύ αργά ώστε να θεωρηθεί πρακτικά στην συνθήκη της κεντρομόλου το μήκος του νήματος ίδιο με την ακτίνα καμπυλότητας.
Επιπλέον να προσθέσω στην σπείρα το εξής από παλαιότερο σχόλιο του Διονύση Μητρόπουλου..
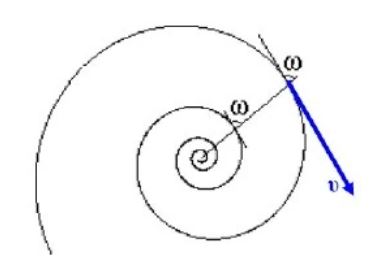
Η στροφορμή ως προς κάποιο σημείο ορίζεται γενικότερα από το εξωτερικό γινόμενο των διανυσμάτων ταχύτητας και θέσης, οπότε το μέτρο της είναι: L=m·υ·r·ημω
όπου ω η γωνία που φαίνεται σχήμα 9 η διατήρηση στροφορμής L1=L2 γράφεται
m·υ1·r1·ημω1= m·υ2·r2·ημω2
Ακόμη λοιπόν κι αν οι γωνίες ω1 και ω2 δεν είναι
90° αλλά παραπλήσιες τότε:
m·υ1·r1= m·υ2·r2
Υπάρχει μάλιστα ένα είδος σπείρας (η ισογώνια ή
λογαριθμική σπείρα) όπου η γωνία ω παραμένει
σταθερή. (η spira mirabilis κατά Bernoulli !)
Καλημέρα Χρήστο.
Ευχαριστώ.