-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Σκοποβολή στο μαγνητικό πεδίο. πριν από 1 μέρα, 9 ώρες
Γεια σου Γιάννη, όμορφη η ανάρτηση και επίσης όμορφη και η λύση του Γιώργου.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Δύο βιβλία σε επαφή και ο λείος κατακόρυφος τοίχος πριν από 1 μέρα, 9 ώρες
Καλημέρα Μίλτο, πολύ όμορφη!
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Ένας μικρός μαγνήτης αφήνεται πάνω από οριζόντιο δαχτυλίδι πριν από 1 μέρα, 9 ώρες
Πολύ ωραία ανάρτηση Ανδρέα.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κ.Χ.Ο. δίσκων και Η.Ε.Δ. από επαγωγή πριν από 1 μέρα, 9 ώρες
Ευχαριστώ Αποστόλη.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κ.Χ.Ο. δίσκων και Η.Ε.Δ. από επαγωγή πριν από 3 μέρες, 10 ώρες
Καλά Σαββατοκύριακο και καλές απόκριες. Σε ευχαριστώ Διονύση για το σχολιασμό, πράγνατι αυτή η εικόνα μου έδωσε την ιδέα της άσκησης.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κ.Χ.Ο. δίσκων και Η.Ε.Δ. από επαγωγή πριν από 3 μέρες, 21 ώρες
Ευχαριστώ Γιάννη, χαίρομαι που σου αρέσει.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Ένα βιβλίο σε επαφή με κατακόρυφο τοίχο. πριν από 4 μέρες, 6 ώρες
Γεια σου Διονύση. Πολύ όμορφη άσκηση που καλύπτει τα πάντα σε σχέση με την τριβή σε ενα όχι και τόσο συνηθισμένο περιβάλλον.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κ.Χ.Ο. δίσκων και Η.Ε.Δ. από επαγωγή πριν από 4 μέρες, 8 ώρες
Καλημέρα Χρήστο σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει. Την ιδέα όντως στην πήρα από τους τροχούς των τραίνων. Θα γράψω ότι τα άκρα της ράβδου έχουν κατάλληλα αρθρωθεί. Το σχήμα δεν το αλλάζω γιατί θεωρώ πως δεν θα έκανε μεγάλη διαφορά.
-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 4 μέρες, 10 ώρες
Κ.Χ.Ο. δίσκων και Η.Ε.Δ. από επαγωγή
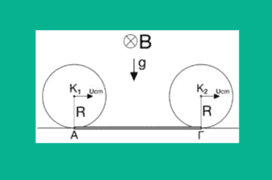Δύο ίδιοι ομογενείς δίσκοι ακτίνας R = 0,25 m εκτελούν κύλιση χωρίς ολίσθηση πάνω σε οριζόντιο επιπέδο με την ίδια σταθερή ταχύτητα του κέντρου μάζ […] -
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Δυο πειράματα με δακτύλιους πριν από 1 εβδομάδα, 1 μέρα
Γεια σου Ανδρέα, ωραίος ο τρόπος να δημιουργηθεί μεταβαλλόμενο ρεύμα και ΗΕΔ από επαγωγή.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Πώς θα κινηθεί η ράβδος; πριν από 1 εβδομάδα, 1 μέρα
Γεια σου Αποστόλη, πολύ όμορφη!
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κλείνοντας έναν – έναν τους διακόπτες. πριν από 1 εβδομάδα, 2 μέρες
Γεια σου Διονύση πολύ όμορφη και χρήσιμη ανάρτηση. Με μια άσκηση μελετάς πως επηρεάζει ενα κύκλωμα το κλείσιμο του διακόπτη σε συνδυασμό και με βραχυκύκλωμα.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Παράλληλα επιβραδύνεται, σε σειρά επιταχύνεται… πριν από 1 εβδομάδα, 2 μέρες
Καλημέρα, πολύ ωραία ανάλυση Χρήστο!
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Τριβή πριν από 1 εβδομάδα, 3 μέρες
Καλημέρα και καλο Σαββατοκύριακο. Ανδρεα χαίρομαι που σου αρέσει η άσκηση και σε ευχαριστώ πολύ για το ip.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Τριβή πριν από 1 εβδομάδα, 4 μέρες
Γεια σου Γιώργο χαίρομαι που σου αρέσει και σε ευχαριστώ πολύ για την αναλυτική σου λύση και για τα πολύ όμορφα συμπεράσματα που κατέληξες, να είσαι καλά!
-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 4 μέρες
-
-
Καλησπέρα Παίλο. Πολύ όμορφη! Μια παρόμοια προσεγγιση φορμαλιστική.
Καταλήγει ότι αυτος ο λόγος είναι ανεξάρτητος της γωνίας κλίσης φ:https://i.ibb.co/tMBsZpJz/feb-90.png -
Γεια σου Γιώργο χαίρομαι που σου αρέσει και σε ευχαριστώ πολύ για την αναλυτική σου λύση και για τα πολύ όμορφα συμπεράσματα που κατέληξες, να είσαι καλά!
-
Καλημέρα Παύλο. Ωραία άσκηση για το ρόλο της στατικής τριβής. Για πολύ καλούς μαθητές προφανώς, γιατί οι περισσότεροι δεν καταλαβαίνουν το ρόλο της στατικής τριβής οπυτε στο βάδισμα.
Έφτιαξα και ένα i.p. ΕΔΩ
Βλέπουμε ότι η στατική τριβή- σε λείο κεκλιμένο παραμενει μηδενική και στην κάθοδο.
- σε τραχύ κεκλιμένο αλλάζει φορά στην κάθοδο.
-
Καλημέρα και καλο Σαββατοκύριακο. Ανδρεα χαίρομαι που σου αρέσει η άσκηση και σε ευχαριστώ πολύ για το ip.
-
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Η ταχύτητα μετά το τέντωμα του νήματος πριν από 1 εβδομάδα, 5 μέρες
Γεια σου Γιώργο, άλλη μια λύση.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κίνηση φορτισμένου σφαιριδίου πριν από 1 εβδομάδα, 6 μέρες
Γεια σου Διονύση, πολύ όμορφη άσκηση.
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Κίνηση αγωγού εντός Ο.Μ.Π. πριν από 1 εβδομάδα, 6 μέρες
Γεια σου Απόστολε. Σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει η άσκηση. Καλές σπουδές εύχομαι!
-
Ο/η Παύλος Αλεξόπουλος σχολίασε το άρθρο Ανάλυση δυνάμεων – Νόμοι του Νεύτωνα πριν από 2 εβδομάδες, 2 μέρες
Καλημέρα και καλή Κυριακή. Ανδρέα χαίρομαι που σου αρέσει και σε ευχαριστώ που πρόσθεσες ετικέτες.
- Φόρτωσε Περισσότερα
Καλημέρα Παύλο.
Πολύ ωραίό ερώτημα κατάλληλο για διαγωνισμό.
Μπερδεύτηκα λίγο με την διάταξη και δεν μπορούσα να καταλάβω ότι κινείται η ράβδος. Μήπως στο σχήμα να έβαζες αρθρώσεις και να το περιέγραφες κάπως. Θυμίζει συστοιχία από ρόδες τραίνου.
Καλημέρα Χρήστο σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει. Την ιδέα όντως στην πήρα από τους τροχούς των τραίνων. Θα γράψω ότι τα άκρα της ράβδου έχουν κατάλληλα αρθρωθεί. Το σχήμα δεν το αλλάζω γιατί θεωρώ πως δεν θα έκανε μεγάλη διαφορά.
Εξαιρετική!!
Ευχαριστώ Γιάννη, χαίρομαι που σου αρέσει.
Καλημέρα Παύλο και καλές απόκριες!
Ζόρικη, μου θύμισε παλιό τρένο!
https://i.ibb.co/LhbX22fB/4.png
Καλά Σαββατοκύριακο και καλές απόκριες. Σε ευχαριστώ Διονύση για το σχολιασμό, πράγνατι αυτή η εικόνα μου έδωσε την ιδέα της άσκησης.
Καλημέρα Παύλο. Έξυπνη!
Ευχαριστώ Αποστόλη.