-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες
Αλλάζοντας την τροχιά, κατά την περιφορά
 Μια σφαίρα μάζας 2kg, την οποία θεωρούμε υλικό σημείο, βρίσκεται σε λείο οριζόντιο επίπεδο, δεμένη στο άκρο μη εκτατού νήματος, το οποίο αφού περάσε […]
Μια σφαίρα μάζας 2kg, την οποία θεωρούμε υλικό σημείο, βρίσκεται σε λείο οριζόντιο επίπεδο, δεμένη στο άκρο μη εκτατού νήματος, το οποίο αφού περάσε […] -
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες
Διατηρείται η στροφορμή ως προς άξονα;
 Βλέπουμε ένα κυκλικό σύρμα που το επίπεδό του δεν είναι οριζόντιο. Βλέπουμε και τον κατακόρυφο άξονα που περνάει από το κέντρο του. Μια χάντρα με τρύ […]
Βλέπουμε ένα κυκλικό σύρμα που το επίπεδό του δεν είναι οριζόντιο. Βλέπουμε και τον κατακόρυφο άξονα που περνάει από το κέντρο του. Μια χάντρα με τρύ […]-
Καλησπέρα Γιάννη.
Δύο σημεία.
1) Έχουμε στροφορμή (και ΑΔΣ) ως προς σημείο και απλά μερικές φορές μας συμφέρει να πάρουμε και να δουλέψουμε με την προβολή της πάνω σε κάποιον άξονα.
2) Όταν έχουμε νήμα, είναι γνωστή η τάση του νήματος και η μηδενική της ροπή ως προς το σημείο πρόσδεσης. Όταν έχουμε το σύρμα, πώς ξέρουμε ότι η δύναμη απο το σύρμα δεν έχει ροπή; -
Καλησπέρα Διονύση.
Ξέρουμε ότι η δύναμη από το σύρμα έχει ροπή, διαφορετικά θα είχαμε διατήρηση στροφορμής ως προς τον εν λόγω άξονα.
Γιατί όμως έχει;
Από που περνάει η δύναμη από το σύρμα; -
Καλησπλερα Γιάννη. Πρεπει η δυναμη απο το δακτύλιο να είναι κάθετη σε αυτόν. Και απο τις άπειρες διευθύνσεις πρεπει να είναι κατακόρυφη λόγω του βαρους της χάντρας. Αρα υπαρχει συνιστωσα που επιταχύνει την χαντρα ,όταν βρισκεται πάνω και συνιστώσα που επιβραδύνει όταν βρίσκεται η χάντρα στο κάτω μέρος
-
Γιώργο σωστά αλλά γιατί δεν διατηρείται η στροφορμή;
Από που περνάει η δύναμη αυτή;
Κάνω ήδη σχήμα…. -
Καλησπέρα.
Η χάντρα καθώς περιστρεφεται έχει γραμμική επιτάχυνση. Δηλ θα πρέπει να δεχεται δύναμη Ν από στεφάνη που να έχει συνιστώσα πάνω στο επιπεδο της στην διεύθυνση της ταχύτητας. Η ροπή αυτης της συνιστωσας ως προς κατακορυφο άξονα δεν είναι 0 -
Μου θυμίζει το θεωρημα των τριών καθέτων.Αν είναι κατακόρυφη , η μια συνιστώσα είναι ακτινική και η αλλη προς τον άξονα που διερχεται από το κεντρο και καθετος στο επίπεδο του κύκλου (η οποία δινει την επιτρόχια συνιστώσα)
-
Πιθανολογώ ότι αυτό έχει να κάνει με τον προσανατολισμό της χάντρας καθώς περιστρεφεται
-
Η δύναμη από το σύρμα είναι κάθετη στο επίπεδο της τροχιάς. Αυτη αναλύεται σε μια κατακόρυφη συνιστώσα παράλληλη στον άξονα και μια ορίζοντα. Η οριζόντια προφανώς έχει ροπή…
πρσοχη στο σχήμα! Οχι στην ανώτερη και κατώτερη θέση!!! Εκεί δεν έχει ροπή.
ειμαι εκτός και δεν μπορώ να σχεδιάσω… -
Στην τελευταία απαρεμβασή μου αυτο το σχήμα προσπάθησα να περιγραψω.
Ετσι όπως το έγραψα ή κατακόρυφη δεν μπορει να αναλυθει σε ακτινική και την αλλη προς τον άξονα που διερχεται από το κεντρο και καθετος στο επίπεδο του κυκλου . Αντιθετα αυτή που είναι προς τον άξονα που διερχεται από το κεντρο και καθετος στο επίπεδο του κυκλου αναλύεται στις άλλες δυο. -
Συμφωνώ με τις παρατηρήσεις σας.
Μου έρχεται πιο εύκολο να μιλήσω (επικαλούμενος το 3ο σχήμα) για ροπή που προκαλεί αύξηση της στροφορμής ως προς τον z άξονα μια και η ροπή (ως προς τον εν λόγω άξονα) είναι θετική. -
Καλησπέρα, ενδιαφέρον θέμα!
Κάποια επιπλέον στοιχεία:
https://i.ibb.co/nNJLGk8c/image.jpg -
Γεια σου Χρήστο.
Χαίρομαι για την επάνοδό σου.
Να υποθέσω ότι επικαλείσαι διατήρηση ενέργειας. -
Να’σαι καλά Γιάννη!
Λύνουμε τον 2ο Νόμο του Νεύτωνα. Παίρνουμε τη δύναμη Ν
κάθετη στην ταχύτητα υ και καταλήγουμε στα παραπάνω.
Αν εργαστούμε με ΑΔΜΕ, καταλήγουμε στα ίδια.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 2 μέρες
Ερωτήσεις κινηματικής
 Μια σφαίρα κινείται κατά μήκος ενός προσανατολισμένου άξονα x, με θετική την προς τα δεξιά κατεύθυνση. Με δεδομένο ότι η επιτάχυνση της σφαίρας, όπου υπά […]
Μια σφαίρα κινείται κατά μήκος ενός προσανατολισμένου άξονα x, με θετική την προς τα δεξιά κατεύθυνση. Με δεδομένο ότι η επιτάχυνση της σφαίρας, όπου υπά […] -
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 3 μέρες
Βρείτε το λάθος
 Χαριτωμένο από το Mind your decisions.
Χαριτωμένο από το Mind your decisions.-
το sqr[(-1) * (-1)] = sqr(-1)*sqr(-1) δεν ισχύει.
sqr(αβ)= sqrα*sqrβ ισχύει μονο για α>0 και β>0 -
Αυτό δίνει και η σελίδα:
Can you find the mistake? -
Αυτο θυμαμαι απο τις ιδιότητες των ριζών
Σελιδα 71 αλγεβρα σχολικού Α λυκείου
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 3 μέρες
Μπορούμε να προκαλέσουμε ανακύκλωση;
 Το μπαλάκι κρέμεται από το Ο μέσω ιδανικού νήματος. Είναι αρχικά ακίνητο. Έχουμε δει ότι ασκώντας σταθερή δύναμη όση το βάρος, φτάνει στην οριζόντια θέση […]
Το μπαλάκι κρέμεται από το Ο μέσω ιδανικού νήματος. Είναι αρχικά ακίνητο. Έχουμε δει ότι ασκώντας σταθερή δύναμη όση το βάρος, φτάνει στην οριζόντια θέση […]-
Καλημέρα Γιάννη. Νομίζω πως όχι, αφού το έργο και των δύο δυνάμεων μέχρι την ανώτατη θέση είναι μηδενικό.
-
Καλημέρα Αποστόλη.
Φυσικά δεν μπορούμε.
Όπως το λες. Ακινητοποιείται πριν την κατακόρυφη θέση.
Διαφορετικά λίγο:
Αν έφτανε με κάποια ταχύτητα στην κατακόρυφη θέση, τότε το έργο των δύο δυνάμεων θα ήταν θετικό.
Όμως της F το έργο είναι μηδέν (μέχρι την κατακόρυφη θέση) και το έργο του βάρους αρνητικό. -
Έγραψα λάθος βέβαια. Το συνολικό έργο των δυναμων είναι αρνητικό…
-
Δεν έγραψες λάθος.
Μηδέν είναι μέχρι τη θέση ακινητοποίησης.
Μια θέση που είναι αισθητά πριν την κατακόρυφη. -
Καλημέρα Γιάννη. “Λογικά” όχι.
Το έργο της δύναμης μεχρι το ανώτερο σημείο είναι μηδέν .Έργο βάρους αρνητικό ,έργο τάσης ,μηδεν ,αρχική κινητική ενέργεια μηδέν. Αρα κινητική ενέργεια αρνητική στο ανώτερο σημειο, πράγμα αδύνατον οποία τιμή και αν έχει η δυναμη -
Καλημέρα Γιώργο.
Ακριβώς. -
καλησπέρα Γιάννη
νομίζω ακινητοποιείται στην οριζόντια θέση, όπου τα έργα των δυνάμεων είναι ίσα και αντίθετα, άρα το συνολικό είναι μηδέν -
Βαγγέλη ακινητοποιείται στιγμιαία σε κάποια θέση η οποία καθορίζεται από τον λόγο F/w.
Με πολύ μεγάλες F πλησιάζουμε την κατακόρυφη θέση, χωρίς να την ξεπεράσουμε. -
Καλημέρα Γιώργο,
Πλήρης απάντηση. -
Καλημέρα
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 4 μέρες
Η στροφορμή και η αλλαγή τροχιάς.
 Μια μικρή σφαίρα μάζας m=0,4kg την οποία θεωρούμε υλικό σημείο αμελητέας ακτίνας, συγκρατείται στη θέση (A), δεμένη στο άκρο οριζόντιου μη εκτα […]
Μια μικρή σφαίρα μάζας m=0,4kg την οποία θεωρούμε υλικό σημείο αμελητέας ακτίνας, συγκρατείται στη θέση (A), δεμένη στο άκρο οριζόντιου μη εκτα […]-
Αφιερωμένη στο Χρήστο Αγριόδημα, για την πρόβλεψή του!
-
Καλημέρα Διονύση. Πολύ καλή η παραλλαγή στις τελευταίες αναρτήσεις στο θέμα. Ειδικά το ερώτημα iii. Αν γίνει σε οριζόντιο επίπεδο έχουμε και διατήρηση στροφορμής, μετά το καρφί, οπότε βγαίνει και άλλη παραλλαγή.
Έχω κενό και μόλις διόρθωσα γραπτό μαθητή στην ομαλή κυκλική. Πήρε το π για άγνωστο και το υπολόγισε, βρίσκοντας π = 1! Θα του αφαιρέσω 3,14 από τη βαθμολογία, μήπως και το μάθει… -
Καλό απόγευμα Ανδρέα.
Δηλαδή το π δεν μπορεί να πάρει την τιμή 1, παρά μόνο το x μπορεί να παίρνει διάφορες τιμές στις εξισώσεις;
Το διεύρυνε το παιδί 🙂 -
Διονύση καλησπέρα.
Σε ευχαριστώ για ρην αφιέρωση.
Πολύ καλή η συνέχεια της πρώτης. Είμαι υπερ γενικά να περνάς κάτι μέσω μιας εφαρμογής – άσκησης. Νομιζω περνά και πιο εύκολα στους μαθητές. -
Καλημέρα Χρήστο.
“Είμαι υπέρ γενικά να περνάς κάτι μέσω μιας εφαρμογής – άσκησης. Νομίζω περνά και πιο εύκολα στους μαθητές.”
Συμφωνώ απολύτως!
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 6 μέρες
Δύο ερωτήσεις κατάταξης στο ίδιο θέμα
 Ερώτηση 1η: Σε έναν ευθύγραμμο δρόμο τριών λωρίδων κινούνται παράλληλα τρία αυτοκίνητα Α, Β και Γ με την ίδια ταχύτητα υ0. Σε μια στιγμή t0 […]
Ερώτηση 1η: Σε έναν ευθύγραμμο δρόμο τριών λωρίδων κινούνται παράλληλα τρία αυτοκίνητα Α, Β και Γ με την ίδια ταχύτητα υ0. Σε μια στιγμή t0 […]-
Καλημέρα Διονύση πολύ όμορφη ανάρτηση απαλλαγμένη από μαθηματικά που εστιάζει στην λογική και την κατανόηση των κινήσεων.
-
Καλημέρα Διονύση.
Συνήθως αφήνεις …”χώρο” για εναλλακτικό συμπλήρωμα στην 2η ,όπως στην 1η ερώτηση.
Κατατάσσοντας τα χρονικά διαστήματα …γραφικά !
https://i.ibb.co/cXyqkvcJ/image.png
Καλή εβδομάδα
(Δεν μιλάς για σταθερές επιταχύνσεις αλλά ουδόλως ενοχλεί) -
Καλημέρα και από εδώ Παύλο, καλημέρα Παντελή.
Παντελή ξεκίνησα να γράφω την άσκηση, δίνοντας καμπύλη τη μεταβολή της ταχύτητας στα κινητά Α και Β.
Αλλά στη διάρκεια της επεξεργασίας σκέφτηκα ότι απλά θα δυσκολέψει ένα μαθητή, ο οποίος πιθανόν να πει, ότι αυτές οι κινήσεις είναι εκτός ύλης, οπότε δεν…
Έτσι το άλλαξα, δίνοντας σταθερές επιταχύνσεις, αφού αυτό φαντάζει πιο εύκολο, ενώ στην πραγματικότητα ούτε δίνει κάποια επιπλέον πληροφορία, ούτε και λείπει κάτι. Απλά μια εικόνα… -
Καλημέρα Διονύση. Πολύ ωραία!
-
Καλημέρα Διονύση.
Χρησιμότατη και διδακτικότητη.
Τα απλά είναι και τα πιο ωφέλιμα. Είναι και τα πιο Φυσικά. -
Ωραία η σκέψη, δύσκολη η μελέτη.
Μου άρεσε το τελικό σχήμα, η κάτοψη είναι ο καλυτερος τρόπος να δοθεί σχήμα σε δύο (και παραπάνω ..) σώματα που κινούνται ταυτόχρονα.
-
Καλό μεσημέρι συνάδελφοι.
Δημήτρη, Χριστόφορε και Κώστα σας ευχαριστώ για το σχολιασμό και την θετική υποδοχή.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 3 εβδομάδες, 2 μέρες
Η στροφορμή και οι ρυθμοί μεταβολής της
 Μια σφαίρα μάζας m=2kg, η οποία θεωρείται υλικό σημείο αμελητέας ακτίνας, κρέμεται στο άκρο μη εκτατού νήματος μήκους l=2m, το άλλο άκρο του οποίου έχει […]
Μια σφαίρα μάζας m=2kg, η οποία θεωρείται υλικό σημείο αμελητέας ακτίνας, κρέμεται στο άκρο μη εκτατού νήματος μήκους l=2m, το άλλο άκρο του οποίου έχει […]-
Καλημέρα Διονύση, έχεις βάλει κάμερες στις τάξεις;;;;
Μπαίνω την άλλη ώρα να κάνω στροφορμή !!!!!
Πολύ καλή…
-
Θοδωρή πρόσεξε γιατί ο Διονύσης έχει ξεχάσει στο iii) να πει ως προς πιο σημείο ζητά την στροφορμή και τον ρυθμό μεταβολή της.
Βέβαια στο i) το αναφέρει. -
Καλημέρα Θοδωρή, καλημέρα Γιώργο.
Σας ευχαριστώ για το σχολιασμό.
Θοδωρή χαίρομαι που το “πέτυχα” αφού η απουσία μου από τις αίθουσες μου δημιουργεί ένα πρόβλημα, που βρίσκονται τα σχολεία, ώστε να μην κάνω άκαιρες αναρτήσεις…
Γιώργο, όποιος δεν έχει μυαλό, έχει ποδάρια και όποιος ξεχνάει να πάρει τα γυαλιά Ηλίου και βγαίνει βόλτα, γυρίζει και τα παίρνει 🙂 -
Kαλημερα Διονυση Θοδωρή και Γιώργο.Διονύση πολυ καλη ασκηση οπως αλλωστε ολες που κατασκευαζεις.
Ως προς το ερωτημα ii.να κανω ενα σχόλιο. Στο σχημα βλεπω δυο σταθερες δυναμεις.Την F και την W. To εργο της W οπως γραφεις ειναι το εργο μιας συντηρητικής δύναμης και ισουται με -Wh οπου h η κατακόρυφη απόσταση μεταξύ των σημείων Α και Β. Η F βεβαιως ειναι μεν σταθερη δυναμη αλλα δεν θα την καλεσω συντηρητικη. Αν την καλεσω συντηρητικη,τοτε θα ξεκινησει μια συζητηση η οποια θα διαρκεσει μεχρι την επομενη συναντηση μας στην ταβερνα. 🙂 Ο βασικος μαθηματικος τροπος ομως υπολογισμου του εργου ειναι ενας και δεν μπορει να δινει αλλο αποτελεσμα για την μια σταθερη δυναμη και αλλο αποτελεσμα για την αλλη σταθερη δυναμη .Δεν μιλαω για δυναμικα ουτε τα οριζω. Αρα το εργο της F ειναι Fx. Συμφωνεις με αυτη την δικαιολογηση; Συναδελφοι συμφωνειτε; 🙂 -
Kαλημέρα Κωνσταντίνε.
Ο μαθητής που θα μπορέσει να κάνει τον συλλογισμό σου είναι πανέξυπνος.
Οταν μεγαλώσει θα γίνει Κωνσταντίνος.Θα μπορούσε ή και θα έπρεπε να ειπωθεί η αντιστοιχία αυτή στην τάξη.
Όμως στην περίπτωση που η δύναμη έχει μεν σταθερό μετρο αλλά εφάπτεται στην τροχιά ο συλλογισμός προφανώς δεν λειτουργεί.
Θα πρέπει όμως ο μαθητής να μπορεί να υπολογίζει το έργο σε αυτήν την περίπτωση.
Η μέθοδος Διονύση τον βοηθά να πει τελικά ότι το εργο δύναμης σταθερού μέτρου που εφάπτεται στην τροχιά ειναι δύναμη επι μήκος τροχιας. -
Γεια σου Γιωργο.Αν η δυναμη εφαπτεται στην καμπυλη τροχια η δυναμη δεν ειναι σταθερη.Τοτε τα πραγματα ειναι διαφορετικα και αυτα που εγραψα φυσικα και δεν λειτουργουν..Εδω στην ασκηση του Διονύση εχουμε δυο σταθερες δυναμεις,την F και την W οι οποιες εχουν ακριβως την ιδια γεωμετρικη σχεση με την τροχια.Καμια απο τις δυο δεν εφαπτεται στην τροχιά.
-
Καλημέρα Κωνσταντίνε.
Νομίζω ότι ο μαθητής θα πρέπει να καταστεί ικανός να υπολογίζει έργο σταθερής δύναμης για μια τυχαία τροχιά, ανεξάρτητα από το αν η δύναμη είναι ή όχι συντηρητική.
Άρα στην απόδειξη και στη μελέτη αυτή, δεν πρέπει να γίνεται, κατά τη γνώμη μου, καμιά αναφορά σε συντηρητικές δυνάμεις, για να μην δοθεί η ευκαιρία… διολίσθησης σε εσφαλμένα συμπεράσματα και σε άλλες ατραπούς…
Προφανώς το τελευταίο που με απασχολεί, στο ζήτημα αυτό, είναι αν μπορεί ο μαθητής εύκολα να χρησιμοποιήσει κάποιο συλλογισμό και να … κόψει δρόμο. -
Εχω την εντυπωση Γιωργο οτι αν η δυναμη εφαπτεται στην τροχια αλλα εχει σταθερο μετρο,μπορεις να πεις δύναμη επι μήκος τροχιας. κατ ευθειαν χωρις αποδειξη,ετσι μου φαινεται.
-
Ενταξει Διονυση κατανοητόν.
-
Καλησπέρα σε όλους.Πολύ όμορφη άσκηση! Πιστεύω ότι ο καλύτερος (μαθηματικός) τρόπος είναι αυτός που αναπτύσσει στην λύση του ,ο Διονύσης.
Ο άλλος τροπος ,”για να κοψεις δρόμο”, ειναι από τον ορισμό: Αν ορίσουμε σαν εργο σταθερής δύναμης το γινόμενο της δύναμης επι την προβολή της τροχιάς του σημείου εφαρμογής της δύναμης στη διεύθυνση της δυναμης(θετικό αν αυτή είναι στην ίδια φορα με την δύναμη, αρνητικό αν έχει αντίθετη φορά) , τοτε καταλήγουμε, αμέσως ,σε αυτο που αναφέρει ο Κωνσταντίνος. -
Καλησπέρα Διονύση.
Πολύ διδακτική που αναδεικνύει και γνωσεις απο προηγούμενες τάξεις. Να προβλέψω η δύναμη να γίνει εφαπτομενικη στην τροχιά και να υπολογιστεί πάλι το έργο;
Και οσο για το οτι ο Διονύσης ειναι εκτος σωματικα απο τις τάξεις πνευματικά ειναι πιο μεσα απο τον καθένα μας. -
Καλησπέρα Διονύση. Την ίδια απορία θα εκφράσω με το Θοδωρή. Σήμερα τους έκανα την άσκηση του Αποστόλη Η στροφορμή και ο ρυθμός μεταβολής της
Το Γ μέρος έχει σταθερή δύναμη, αλλά η κίνηση γίνεται σε οριζόντιο επίπεδο. Ένας μαθητής ρώτησε, πως λύνεται αν η σφαίρα κρέμεται από το ταβάνι. Του είπα θα το δούμε στο επόμενο μαθημα. Και νάτη η άσκηση έτοιμη…
Το έργο του βάρους διδάσκεται ως διαφορά δυναμικών ενεργειών, οπότε εξηγείται γιατί Wβ = -mgΔh.
Το έργο της F δε μπορεί να εξηγηθεί έτσι, άρα θέλει ένα αποδεικτικό ερώτημα για τον τύπο.
Η στροφορμή εξαρτάται από τη γωνία φ του νήματος με την κατακόρυφο. Έκανα τη γραφική παράσταση με το graph. Πράγματι βλέπουμε την τιμή της στις 37 μοίρες 8kgm^2/s και αρνητικό ρυθμό μεταβολής.
https://i.ibb.co/Xf0jmVXZ/image.jpg -
Καλησπέρα Διονύση.Σε ανάρτησή σου στις 31/10/24 έχεις διατυπώσεις την άποψη:Και που να ξέρει Διονύση ο μαθητής το έργο σταθερής δύναμης σε καμπύλη τροχιά;Τί άλλαξε;
-
Γεια σας και πάλι. Η στροφορμή με τους περιορισμούς που έχουν θέσει στη
διδασκαλία της φαντάζει ως ένα μέγεθος που δύσκολα γίνεται αντιληπτή
σε πρώτο χρόνο η ανάγκη εισαγωγής του.Οι μαθητές για να κατανοήσουν τον λόγο διδασκαλίας της στροφορμής χρειάζονται
παραδείγματα όπου η στροφορμή του σώματος διατηρείται, ενώ η ταχύτητα μεταβάλλεται, όπως στη σπειροειδή τροχιά σφαίρας δεμένης στο άκρο νήματος σε λείο οριζόντιο δάπεδο, όταν το νήμα διέρχεται από την οπή και ασκώντας κατάλληλη δύναμη μεταβάλλουμε το μήκος του.Ακόμα καλύτερα, όταν σε μία κρούση διατηρείται η στροφορμή του συστήματος ως προς τον άξονα περιστροφής, αλλά όχι η ορμή των σφαιρών που συγκρούονται…
Εδώ βέβαια, γίνονται οι γνωστές αλχημείες με την αβαρή ράβδο και το στερεό ράβδος-μάζες σφηνωμένες στη ράβδο…Διονύση, περιμένουμε μία ανάλογη ανάρτηση, διατήρησης της στροφορμής αλλά όχι της ορμής….
Στη συγκεκριμένη ανάρτηση θα είχε ενδιαφέρον ένα ερώτημα:
“Ποια το ελάχιστο μέτρο της δύναμης F, ώστε η ράβδος να φθάσει στη θέση, όπου θα μηδενιστεί η ροπή της F, ενώ η ροπή του βάρους θα αποκτήσει μέγιστο μέτρο, αντίθετα δηλαδή με ό,τι ίσχυε στην αρχική θέση”
-
Καλημέρα σε όλους.
Χρήστο, Ανδρέα, Θύμιο και Θοδωρή σας ευχαριστώ για το σχολιασμό και τις τοποθετήσεις.
Θύμιο και τώρα λέω “Και που να ξέρει ο μαθητής το έργο σταθερής δύναμης σε καμπύλη τροχιά;”
Υπάρχει κάποια παράγραφος ή κάποια εφαρμογή που να διδάσκεται στο σχολείο που να αναφέρεται στο θέμα; Όχι. Και τότε;
Και τότε έρχεται μια άσκηση, όπως αυτή εδώ, η οποία αντιμετωπίζει το ερώτημα από “μηδενική βάση” Να αποδειχτεί ότι…
Άσκηση είναι Θύμιο!
Και μέσω μιας τέτοιας άσκησης μπορεί να καλυφτεί το κενό για έναν μαθητή, o οποίος προφανώς πρέπει να εμπλακεί… -
Θοδωρή επανέρχομαι, πηγαίνοντας 3 χρόνια πριν:
Μια κρυμμένη στροφορμή
Τι λες, σου κάνει;;
Διατηρείται η στροφορμή, αλλά όχι η ορμή… (και δεν έχει και αβαρή ράβδο) 🙂 -
Καλημέρα Διονύση. Είμαι κατά ένα μάθημα πίσω από τους συναδέλφους, αλλά σύντομα θα αξιοποιηθεί!
Πολύ διδακτική, ευχαριστούμε! -
Καλό απόγευμα Μίλτο.
Χαίρομαι που σου άρεσε και που πρόκειται να χρησιμοποιηθεί… -
Καλησπέρα Διονύση.Η απόδειξη της προηγούμενης ανάρτησης ήταν για το έργο δύναμης σταθερού μέτρου διαρκώς εφαπτόμενης σε καμπύλη τροχιά(Δικιά μου ή όχι πάντως υπάρχει).Το ίδιο τετριμμένο είναι η απόδειξη του έργου σταθερής δύναμης σε καμπύλη τροχιά.Άν η προηγούμενη απόδειξη είναι εκτός πώς αυτή η απόδειξη είναι εντός;
-
Σύ ύπας
-
Καλησπέρα σε όλους.Σχετικα με τις παρατηρήσεις του Θύμιου έχω να πω το εξής:Δεν χρειάζεται να ξέρει ο μαθητής να κάνει έναν υπολογισμό ενός επικαμπυλιου ολοκληρώματος με εκλαϊκευμένη διατύπωση..Δεν έχει ερωτηθεί ποτέ σε εξετάσεις και ούτε πρόκειται. Είναι τεχνικό βήμα και μόνο Μαθηματικά όχι Φυσικη.Τα παιδιά Υγείας δεν έχουν ιδέα από τέτοια πράγματα.Δεν το έχω κάνει ποτέ στην τάξη και ούτε θα το κάνω με τα υπάρχοντα αναλυτικά προγράμματα. Όμως στην περίπτωση δύναμης σταθερού μέτρου και συνεχώς εφαπτομένης σε καμπύλη τροχιά,τα πράγματα είναι μαλλον πιο απλά αφού μπορεί την τροχιά να την τεντωσεις να γίνει ευθεία και είναι εύκολο να δεις ότι δεν αλλάζει τιποτα.Ουτε αυτό θα ερωτηθεί βεβαίως αλλά είναι πιο απλό να εξηγηθεί.Δεν παριστάνω τον μάντη αλλά προτιμώ να αφιερώσω χρόνο σε πιο πιθανά ερωτήματα.
-
Αφού μιλάμε για στροφορμή δείτε εδώ, ειδικά την 4η επανάληψη της φάσης,
όπου φαίνεται ξεκάθαρα η ιδιοπεριστροφή της μπάλας…Spin όχι αστεία
-
Θύμιο γράφεις: “Άν η προηγούμενη απόδειξη είναι εκτός πώς αυτή η απόδειξη είναι εντός”. Μάλλον δεν διάβασες την προηγούμενη απάντησή μου.
Ας το διατυπώσω αλλιώς λοιπόν.
Δίνω μια άσκηση, όπου σε ένα ερώτημα διαπραγματεύεται το έργο δύναμης σε καμπύλη τροχιά. Δεν είπα ότι υπάρχει η απόδειξη στο βιβλίο και ότι ο μαθητής ωφείλει να την γνωρίζει! Αν ήταν απόδειξη του βιβλίου, δεν θα υπήρχε λόγος να την ζητήσω σε άσκηση.
Το αν αυτό είναι ένα πιθανόν θέμα εξετάσεων Κωνσταντίνε, προφανώς δεν με απασχολεί. Δεν έβαλα το θέμα στις εξετάσεις, ούτε είμαι μέλος της ΚΕΕ 🙂 που θα βάλει θέματα.
Ούτε όμως ποτέ επεδίωξα να “πιάσω θέματα”!!!
Αν κάποιος παρακολουθεί τις αναρτήσεις μου θα δει ότι απέχουν πολύ από το ύφος και το στυλ των θεμάτων των τελευταίων χρόνων. Αλήθεια πιστεύει κάποιος ότι δεν έχω καταλάβει, τόσα χρόνια, ποιες προδιαγραφές έχουν τα Δ κυρίως θέματα; Ή νομίζει κάποιος ότι δεν μπορώ να γράψω Δ θέμα υπερπαραγωγή, ώστε να έχει πολύ μεγάλη “ζήτηση” αφού θα προσπαθεί να πιάσει το θέμα;;;
Να πω τέλος, ότι προφανώς ΔΕΝ επέβαλα σε κάποιον να διδάξει το παραπάνω θέμα… Το τι διδάσκει ο κάθε συνάδελφος είναι δική του επιλογή και ευθύνη… -
Γεια σου Διονύση, πολύ όμορφη και πολύ χρήσιμη ανάρτηση.
-
Καλό απόγευμα Παύλο.
Σε ευχαριστώ. -
Διονύση συμφωνώ η ανάρτηση είναι άριστη απλώς είπα για το συγκεκριμένο ερώτημα ότι εκτιμώ ότι δεν αποτελεί πιθανό θέμα εξετάσεων χωρίς αυτό να σημαίνει ότι βλάπτει να το διαβάσει ένας μαθητής ειδικά θετικής.Απλως εγώ σε μικτό ακροατήριο δεν δείχνω τέτοιους υπολογισμους
-
Καλησπέρα Διονύση.
Εξαιρετική άσκηση. -
Καλημέρα Κωνστανίνε. Κατανοητόν.
Καλημέρα και καλή βδομάδα Χριστόφορε. Χαίρομαι που σου άρεσε. -
Διονύση, καλημέρα. Η ανάρτησή σου «τα έχει όλα και συμφέρει».
Πράγματι, αναδεικνύει πολλά «λεπτά» ζητήματα που συνήθως μας διαφεύγουν κατά τη διδασκαλία, ενώ οι μαθητές δεν είναι εξοικειωμένοι.
(επ’ ευκαιρία της επικοινωνίας μας: για τον «ημίθεο» Σαββόπουλο διαβάζω απίθανα πράγματα, ο καθένας βλέπει ότι θέλει και αυτό δεν είναι κακό κατ’ αρχήν, αλλά ας αφήνουν και τους υπόλοιπους να κάνουν το ίδιο).
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 3 εβδομάδες, 3 μέρες
Όταν δίνεται το διάγραμμα θέσης κινητού
 Κατά μήκος ενός προσανατολισμένου άξονα κινείται ένα σώμα και στο διάγραμμα δίνεται η θέση του σε συνάρτηση με το χρόνο. Δίνεται ότι το σώμα κ […]
Κατά μήκος ενός προσανατολισμένου άξονα κινείται ένα σώμα και στο διάγραμμα δίνεται η θέση του σε συνάρτηση με το χρόνο. Δίνεται ότι το σώμα κ […]-
Καλημέρα Διονύση.
Στην πρώτη ματιά το διάγραμμα Χ-t …”ξενίζει” και
απαιτεί Δt>0 για συνειδητοποίηση της κίνησης.
Να εξομολογηθώ… πρώτα σχεδίασα ποιοτικά το υ-t
κάτω από το χ-t με το σκεπτικό:
1) ότι η α είναι σταθερή θετική
2) ότι υ<0 μέχρι την t1 όπου υ=0 (κλίση υ-t ) και μετά υ>0
Η δομή του θέματος απαιτεί καλά συνειδητοποιημένο μαθητή
στις κινήσεις και πέρα του παραπάνω σκεπτικού μου, να
έχει τη γνώση πως δύο εξισώσεις καθορίζουν γενικά τις ευθύγραμμες κινήσεις οπότε ,όπως έδρασες, στην Δχ-t γνωρίζει τα Δχ ,t , α άρα βγήκε η υ0 !
(Στην 4η σειρά της λύσης του i) γράφεις σταθερήταχύτηταεπιτάχυνση )
Να είσαι καλά -
Καλημέρα Παντελή, σε ευχαριστώ για το σχολιασμό και την ενασχόληση με το θέμα!
Αλλά και για την επισήμανση για την λάθος λέξη… -
Καλημέρα Διονύση.Πολύ Όμορφη.
Προσωπικά αυτή η ασκηση θεωρώ ότι είναι ιδανική για να φανεί πως χρησιμοποιείται η δευτεροβάθμια εξίσωση στη Φυσική.
Δηλαδη να χρησιμοποιήθεί:
x=xo+υοt+(1/2)at^2 => x=6+υοt+(1/2)t^2 και για x=0 => υο=-4m/s αρα:
x=6-4t+(1/2)t^2
και ακολουθως να μελετήθεί η δευτεροβαθμια (xmin ,t για xmim, την αλλη χρονική στιγμή που x=0 , τις κλίσεις (προσημο) σε κάποιες χρονικές στιγμές, κλπ). -
Καλό απόγευμα Γιώργο και σε ευχαριστώ για το σχόλιο.
-
Στην κινηματική στερεού, στην περιστροφική κίνηση γύρω από σταθερό άξονα, επιχειρηματολογώντας πως θετική γωνιακή επιτάχυνση δεν σημαίνει κατ’ ανάγκη επιταχυνόμενη κίνηση, σχεδίασα διάγραμμα ω=f(t) ανάλογο με το υ=f(t) που αντιστοιχεί στην άσκηση αυτή. Μετά είπα να σχεδιάσω το Δφ=f(t)….
Αφενός, Παντελή έπιασα τον εαυτό μου για 2-3 sec να αμφιβάλλει, αφετέρου
είδα έκπληξη στα μάτια των περισσότερων σε τμήμα Γθετ….Συνήθως Διονύση, έδινες διάγραμμα υ=f(t) και ζητούσες x=f(t)….
Εδώ, ανέβηκες “πίστα” ….Ισχύουν και για σένα όσα έγραψα στο προηγούμενο σχόλιο στον Παύλο…
Δεν δίνεις κίνητρα η φαντασία πρώτα να ταξιδεύσει και μετά να αφαιρέσει τα περιττά….old school physics …. -
Καλημέρα και από εδώ Θοδωρή και σε ευχαριστώ για το σχολιασμό.
Λες να προλαβαινω να εκσυγχρονιστώ και να ακολουθήσω τις νέες τάσεις;
Δεν το βλέπω, οπότε μάλλον πρέπει να το αφήσω το άθλημα για νεώτερους… -
Και να η απόδειξη!
Έγραψα παραπάνω “νεώτερους”!
Αλλά ρωτώντας την ιδιωτική μου φιλόλογο, μου είπε ότι σήμερα ο εκσυγχρονισμός της γλώσσας, επιβάλει να γράψω “νεότερους”.
Το λέει και ο Μπαμπινιώτης!!!
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 3 εβδομάδες, 4 μέρες
Αντίο στον Νιόνιο της νιότης μας…
 Μια ολόκληρη εποχή σφράγισε ο Διονύσης Σαββόπουλος, ο Νιόνιος, ο μουσικός μύθος της Ελλάδας, ο οποίος έφυγε χθες από τη ζωή, σε ηλικία 81 ετών. Ένας μεγάλος τραγουδοποιός, που άφησε ιστορία. Τα λόγια περιττά.
Μια ολόκληρη εποχή σφράγισε ο Διονύσης Σαββόπουλος, ο Νιόνιος, ο μουσικός μύθος της Ελλάδας, ο οποίος έφυγε χθες από τη ζωή, σε ηλικία 81 ετών. Ένας μεγάλος τραγουδοποιός, που άφησε ιστορία. Τα λόγια περιττά.-
16εξάρης κοπανατζής στην Ηπείρου και Αχαρνών στο Κύτταρο. Απογευματινή παράσταση ειδικά για τους κοπανατζήδες (τότε τα σχολεία λειτουργούσαν και απόγευμα). Η παράσταση άρχιζε με τον Τζίμη τον Τίγρη. Απέναντι η παρέα έσερνε από το καφενεδάκι τον Νιόνιο για να μας τραγουδίσει κομμάτια από το φορτηγό αλλά και το Μπάλο…..
Ένα κομμάτι της ζωής μας έφυγε αλλά ζει ακόμη στις ξεθωριασμένες μνήμες μας… -
Τον άκουσα σε κάποιο Φεστιβάλ Θεσσαλονίκης στην ΕΡΤ να λέει την Παράγκα, νομίζω ήταν Χούντα ακόμα, δε θυμάμαι πήγαινα Γυμνάσιο. Τον έμαθα το 78, στην Α΄Λυκείου – τον άκουγαν οι φίλοι μου.
Από το “Φορτηγό” μέχρι τη “Ρεζέρβα”, η εξέλιξη στην ποιότητα των στίχων, των μηνυμάτων και της μουσικής του ήταν απίστευτη.
Δεν υπήρχε μάζωξη, που σε όσους ξέραμε κιθάρα, να μη ζητήσει η παρέα κάποιο τραγούδι του Διονύση.
Μετά τη “Ρεζέρβα” κάπου τον “χάσαμε”. Έβγαλε τα “Τρεαπεζάκια Έξω”. Ο Νιόνιος άλλαξε, η κοινωνία άλλαξε, δεν έχει σημασία. Έδωσε πολλά. Τεράστιος. Μόνο σεβασμό νιώθουμε.Αν ήθελα ένα τραγούδι να αφιερώσω, θα έβαζα την Παράγκα. Από τότε που το άκουσα στο Φεστιβάλ Θεσσαλονίκης μέσα στη Χούντα, μέχρι σήμερα, δεν άλλαξε τίποτα.
Παράγκα -
Το 1975 ήμουν 6 χρονών. Στο σπίτι υπήρχε ένα Tepaz και στη δισκοθήκη διάφορα 45άρια. Ανάμεσά τους και το “Σαν τον Καραγκιόζη” που μόλις είχε κυκλοφορήσει. Άρχισα να το ακούω ξανά και ξανά χωρίς φυσικά να καταλαβαίνω τους στίχους. Ήταν η πρώτη μου επαφή με το Σαββόπουλο και τα τραγούδια του. Νιόνο θα σε τραγουδάμε πάντα.
-
καλό σου ταξίδι, Νιόνιε της νιότης μας
“ένθα ουκ έστι πόνος, ου θλίψη…”
να είσαι καλά αν και όπου είσαι τώρα…
(στα φοιτητικά μου χρόνια, έμενα Αλκιβιάδου, ερχόμουν στο πεζοδρόμιο της Ηπείρου, έξω από τη μπουάτ Κύτταρο, να σε ακούσω, δεν είχα καν χρήματα για το μειωμένο φοιτητικό εισιτήριο, έκανα μεγάλες οικονομίες και κατάφερα να αγοράσω μια κιθάρα, έμαθα να παίζω και να τραγουδώ, αρκετά καλά, μόνο ένα τραγούδι σου, που σου το αφιερώνω
https://www.youtube.com/watch?v=s6Jd1iKPCJc) -
Αυτόν τον Σαββόπουλο θα θυμάμαι
….Κι εσύ έφεγγες στην μέση ολου του κόσμου……
…. η συγκέντρωση ανάβει κι ολα είναι συνειδητά
-
Ένα όμορφο έργο του:
ΑχαρνήςΆφησε εποχή το Ζητω το Ελληνικό τραγούδι.
-
Το 2023, ένας άλλος δικός μας, ο Γιάννης Πετρίδης, είχε γράψει:
“Ο Σαββόπουλος φεύγει. Ας φύγει όπως θέλει και ας λέει ό,τι θέλει. Αυτά που έπρεπε, τα είπε στην ώρα τους. Το χώμα δεν ακούει τα λόγια, μόνο τα βήματα. Το χνάρι του βαθύ. Σε πενήντα χρόνια το υπαρξιακό του βέρτιγκο θα έχει ξεχαστεί και θα στέκει μόνο το Περιβόλι του, ο Μπάλος, το Βρώμικο Ψωμί, η Ρεζέρβα, και σπουδαία τραγούδια”.
-
Οι πρώτοι δίσκοι στο σπίτι,τα πρώτα μουσικά ακούσματα…Θυμάμαι την παράφραση που έκανα για μια γιορτή στο Γυμνάσιο…Η Ευανθουλα κλαει πριν κοιμηθεί γιατί έχει μείνει Αρχαία και Φυσική…
Τον θυμόμαστε και μένει στη μνήμη μας για τα έργα του, όπως και τον κάθε επώνυμο καλλιτέχνη, και όχι για τις προσωπικες επιλογές του…
Ένα παραμύθι η ζωή του… -
Μήνες είχα να μπω στην εφαρμογή. Σήμερα μπήκα, χάρις στον Νιονιο που μας άφησε χτες.
Σε ευχαριστώ Διονύση Μαργαρη
https://i.ibb.co/9kFRBXsJ/2025-10-22-174322-1.png -
1967 φιλοξενούμενος για λίγο στο ημιυπόγειο
συμμαθητή μου και φίλου στην Αθήνα, βάζει στο πικαπ
το “φορτηγό” σε χαμηλή ένταση …δεν ξέρω ακριβώς γιατί αλλά
ακόμη και σήμερα φτιάχνω στο νου μου εικόνα με τον Βιετναμέζο που
“…κρυμμένος στο ποτάμι ανασαίνει με καλάμι…”
Στο Βιετνάμ πυρπόλησαν το ρύζι
πυρπόλησαν το ρύζι.
Στη Σαϊγκόν δεν μπόραες να ζήσεις,
δε σου `φτανε ο αέρας για να ζήσεις.Τώρα, κρυμμένος στο ποτάμι, ανασαίνεις,
Φο Μι Τσιν, ανασαίνεις
με καλάμι.Και ύστερα στο…ΚΥΤΤΑΡΟ!
Καλό ταξίδι Νιόνιο … θα σε ακούμε(νε) εδώ ! -
Απόσπασμα από το fb του Αλέξη Χαρίτση
Ωδή στον μεγάλο αντιφατικό
“Τις τελευταίες μέρες «έλιωσα» τους δίσκους του Σαββόπουλου. Είχα χρόνια να το κάνω. Αλλά η συγκίνηση ήταν η ίδια, γνήσια και δυνατή. Όπως και τότε, όπως θα είναι πάντα. Παρόλη την μεγάλη απογοήτευση από την πολιτική του στάση εδώ και χρόνια.
Και τα τραγούδια του δεν γίνεται να πάψουν να αγγίζουν την ψυχή μας, γιατί:
Γεννηθήκαμε με την «Συννεφούλα».
Μεγαλώσαμε με «Μη μιλάς άλλο γι’ Αγάπη» και «Καραγκιόζη».
Μάθαμε μουσικά γράμματα με τον «Μπάλο» και «Το Περιβόλι του Τρελού».
Προσεγγίσαμε το σύμπαν του Ντίλαν και το ροκ συνολικά μέσα από τον «Άγγελο Εξάγγελο» και τον «Παλιάτσο και τον Ληστή».
Συγκινούμασταν όταν βλέπαμε τον πατέρα να δακρύζει κάθε φορά που άκουγε «του ‘60 τους εκδρομείς».
Χορέψαμε μεθυσμένοι το «ροκ ζεϊμπέκικο» της Μπέλου.
Πολιτικοποιηθήκαμε με την «συγκέντρωση της ΕΦΕΕ» και το «Κιλελέρ».
Γι’ αυτό, χθες, την ώρα της κηδείας, επέλεξα να τον αποχαιρετήσω ακούγοντας σε λούπα την αριστουργηματική Ωδή στον Γεώργιο Καραϊσκάκη.
Το θεώρησα πιο τίμιο από το να σταθώ στη Μητρόπολη δίπλα στον Άδωνη Γεωργιάδη και το μισό υπουργικό συμβούλιο και να ακούω τον Κυριάκο Μητσοτάκη να αποχαιρετά τον «φίλο του τον Νιόνιο».
Ακούω την κριτική και την καταλαβαίνω. Παραμένω αμφίθυμος. Αλλά σταθερά συγκινημένος»
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 3 εβδομάδες, 5 μέρες
Σχεδιάστε τις δυνάμεις
 Οι δύο δίσκοι είναι αρθρωμένοι με λείες αρθρώσεις στα άκρα ενός αβαρούς και άκαμπτου σύρματος. Ο μαγνήτης έλκει μόνο τον γκρίζο δίσκο. Σχεδιάστε τις δυνάμεις που το σύρμα ασκεί στους δίσκους.
Οι δύο δίσκοι είναι αρθρωμένοι με λείες αρθρώσεις στα άκρα ενός αβαρούς και άκαμπτου σύρματος. Ο μαγνήτης έλκει μόνο τον γκρίζο δίσκο. Σχεδιάστε τις δυνάμεις που το σύρμα ασκεί στους δίσκους.-
Kαλημερα Γιάννη.Οι Δυναμεις που ασκουνται στο συρμα πρεπει να εχουν συνισταμενη μηδεν και ολικη ροπη μηδεν.Αν δεν συνεβαινε αυτο θα ειχαμε απειρισμο των επιταχυνσεων όπερ Άτοπον. Αρα πρεπει αναγκαστικα οι δυναμεις που ασκουνται στο συρμα να ειναι αντιθετες και να βρισκονται πανω στην διακεντρο.(Υπέθεσα οτι οι αρθρωσεις ειναι στα κεντρα.)Αρα λογω τριτου νομου και οι δυναμεις που ασκουνται στους δισκους πρεπει να ειναι αντιθετες και να βρισκονται πανω στην διακεντρο. Γενικα εχουμε δυο δυνατοτητες. Ομως αν δεν υπηρχε το συρμα οι δυο δισκοι θα απομακρυνοντουσαν και το συρμα ειναι ακαμπτο και θα εμποδισει την απομακρυνση. Αρα οι δυναμεις που το συρμα ασκει στους δισκους ειναι αντιθετες,εχουν φορέα την διακεντρο και εχουν φορά απο το κεντρο του ενος δισκου προς το κεντρο του αλλου δισκου.
-
Καλημέρα Γιάννη.
Ξεκίνησα να απαντήσω στο ερώτημά σου, αλλά είδα την απάντηση του Κωνσταντίνου (καλημέρα Κωνσταντίνε), η οποία με βρίσκει απολύτως σύμφωνο…
Οπότε τι άλλο να προσθέσω; -
Kαλημέρα Διονύση.
-
Καλημέρα.
Μια προσπάθεια. Βλέπω ένα ελεύθερο στερεό. Δέχεται μια δύναμη από μαγνήτη. Αρχίζει να εκτελεί μια κίνηση που θεωρούμε ότι αναλύεται σε μια επιταχυνόμενη μεταφορική και μια στροφική επιταχυνομενη περί το cm. Θα ανεβάσω αργότερα αρχείο…. -
Καλημέρα παιδιά. Σκέφτηκα όπως ο Γιώργος.
-
Καλημέρα παιδιά.
Η λύση που σκέφτηκα ήταν αυτή του Κωνσταντίνου.
Φυσικά είναι σωστή η του Γιώργου. -
Καλά κύριε. Τόση προσπάθεια που ο κύριος Κωνσταντίνος με μια γραμμή καθάρισε!!!
Επίτηδες το έκανα παιδιά για να δω αν … συμφωνώ -
καλησπέρα σε όλους
Γιάννη ερωτήματα:
τα 4 σώματα βρίσκονται στο ίδιο κατακόρυφο ή οριζόντιο (όπως φαίνεται) η πλάγιο επίπεδο;
τα 4 σώματα παραμένουν διαρκώς ακίνητα;
το όποιο επίπεδο έχει τριβές;
το σύρμα δέχεται μαγνητική δύναμη; -
Γεια σου Βαγγέλη.
Μπορείς να υποθέσεις ότι είναι στο κενό και εκτός πεδίου βαρύτητας.
Όμως δεν έχει καμία σημασία αυτό Η συνισταμένη των δύο δυνάμεων θα είναι μηδέν σε κάθε περίπτωση καθώς και η ροπή τους.
Ας είναι σε πλάγιο τραχύ επίπεδο, αρκεί δυνάμεις να δέχονται μόνο τα μπαλάκια.
Η απάντηση αλλάζει αν με κάποιο τρόπο το σύρμα δέχεται και τρίτη δύναμη ή αν οι αρθρώσεις δεν είναι λείες.
-
-
Ο/η Διονύσης Μάργαρης και ο/η
Μπατατέγας Γεώργος είναι πλέον φίλοι πριν από 3 εβδομάδες, 5 μέρες
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 3 εβδομάδες, 6 μέρες
Όταν φορτώνουμε μια σανίδα
 Μια λεπτή ομογενής σανίδα ΑΒ, ισορροπεί όπως στο σχήμα, αρθρωμένη στο άκρο της Α, ενώ το άκρο της Β είναι δεμένο στο κάτω άκρο κατακόρυφου νήματος. Η σαν […]
Μια λεπτή ομογενής σανίδα ΑΒ, ισορροπεί όπως στο σχήμα, αρθρωμένη στο άκρο της Α, ενώ το άκρο της Β είναι δεμένο στο κάτω άκρο κατακόρυφου νήματος. Η σαν […]-
Καλημέρα Διονύση.
Πολύ όμορφη η ισορροπία σου. Ολοκληρωμένο θέμα όπως το παρουσίασες. -
Καλό απόγευμα Χρήστο.
Σε ευχαριστώ για το σχόλιο. -
Όμορφη Διονύση. Αξίζει ίσως να σημειωθεί πως:
-Όταν το νήμα είναι κατακόρυφο στο άκρο της ράβδου, ανεξάρτητα από την κλίση
της σανίδας Τ=F=W/2-Μετακινώντας το σημείο πρόσδεσης από το άκρο Β προς το μέσο Μ, αυξάνεται η
τάση του νήματος Τ>W/2 και μειώνεται η F<W/2-Αν το σημείο πρόσδεσης του νήματος είναι το μέσο Μ, τότε Τ=W και F=0
-Αν το σημείο πρόσδεσης του νήματος είναι μεταξύ Μ και Α τότε Τ>W και η F
θα έχει φορά προς τα κάτωΌλα τα παραπάνω εφόσον το νήμα είναι κατακόρυφο
-
Καλημέρα Θοδωρή και σε ευχαριστώ για το σχολιασμό και την προσθήκη για την τάση του νήματος, όταν αλλάζει το σημείο πρόσδεσης.
Εδώ βέβαια δέσαμε μια και καλή το νήμα και δεν αλλάζουμε σημείο 🙂
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 4 εβδομάδες, 1 μέρα
Μια απλή ή μια σύνθετη κίνηση
 Μια «απλή» κίνηση είναι η πτώση κατά μήκος ενός κεκλιμένου επιπέδου, όπως αυτή του σχήματος. Ο Θωμάς, «πνεύμα αντιλογίας», μαθητής της Β΄ Λυκείου μ […]
Μια «απλή» κίνηση είναι η πτώση κατά μήκος ενός κεκλιμένου επιπέδου, όπως αυτή του σχήματος. Ο Θωμάς, «πνεύμα αντιλογίας», μαθητής της Β΄ Λυκείου μ […]-
Ωραίο θέμα και συναρπαστική η παρουσίαση Διονύση
Προφανώς και ένα φαινόμενο μπορεί να περιγραφεί με πολλούς διαφορετικούς τρόπους . Στο βαθμό που η επεξεργασία είναι σωστή οι προβλέψεις θα είναι ίδιες για τον τρόπο που εξελίσσεται το ίδιο φαινόμενο.
Δυστυχώς εδώ και πολλά χρόνια δεν διδάσκονται η σχετική κίνηση ούτε οι συνέπειες από την επιλογή του συστήματος αναφοράς και του συστήματος περιγραφής.
Προσωπικά ποτέ δεν μου άρεσε αυτή η οπτική της “επελληλίας δυο κινήσεων” και προτιμούσα πάντα την οπτική της επίκλησης της σχετικής κίνησης διαφορετικών παρατηρητών ή διαφορετικών συστημάτων περιγραφής . Διότι και η ομαλή κυκλική κίνηση μπορεί να χρειαστεί να μην την περιγράψουμε σε πολικό σύστημα αναφοράς αλλά σε ορθογώνιο Καρτεσιανό σύστημα …. Τι δηλαδή θα πούμε τότε ότι η ομαλή Κυκλική Κίνηση είναι επαλληλία δυο αρμονικών ταλαντώσεων ; ! Δεν μου κάθεται με τίποτα.Καλημέρα
-
Καλημέρα παιδιά. Διονύση ακολουθείς τη γραμμή των τελευταίων σου αναρτήσεων σχετικά με την περιγραφή μιας κίνησης. Οι Θωμάδες – πνεύματα αντιλογίας – σπανίζουν, αλλά είναι πάντοτε ευπρόσδεκτοι.
-
Καλημέρα παιδιά.
Μήτσο γιατί όχι;
Στον παλμογράφο αλλά και σε μηχανικές διατάξεις συντίθενται δύο αρμονικές ταλαντώσεις με προϊόν μία ομαλή κυκλική κίνηση. -
Για να παίξετε Οι 4 παρατηρητές:
-
Καλησπέρα Διονύση.
Δεν είχα σκεφτεί την 2η απάντηση !
Αφου λοιπόν είδα τους άξονες ,ξεκίνησα να γράφω
τις εξισώσεις με την Ν μέσα ,αλλά αποτέλεσμα δεν έβγαζα,
οπότε κοίταξα τη λύση σου και είδα ότι χρησιμοποιείς την
Ν=mgσυνθ από το σύστημα της 1ης απάντησης!
Προβληματίστηκα όχι για την ορθότητα αλλά για το μη σύνηθες
της αλλαγής συστήματος και τελικά λέω …γιατί όχι.
Καλό Σαββατόβραδο -
@ Γιάννη Κυριακόπουλο
Εντάξει αυτό είχα στο μυαλό μου. Αλλά το άκρο του δευτερολεπτοδείκτη του ρολογιού μου δεν εκτελεί δυο αρμονικές ταλαντώσεις με διαφιορά φάσης π/2 .Στην ερώτηση : “Πόσες κινήσεις εκτελεί ο Πλανήτης Γη ;”
Επειδή δεν αναφέρει η ερώτηση ως προς ποιον παρατηρητή θα απαντούσα : Η θέση της Γής μεταβάλλεται με κάποιον ένα και μοναδικό τρόπο για κάποιον παρατηρητή . Ο παρατηρητής μπορεί να την περιγράψει αυτήν την μια και μοναδική κίνηση με πολλούς τρόπους ( μαθηματικές ή μη περιγραφές ) ανάλογα με το σύστημα περιγραφής ( καρτεσιανών, πολικών, σφαιρικών συντεταγμένων ) ή ακόμα και να επικαλεστεί τις περιγραφές άλλων παρατηρητών των οποίων τις παρατηρήσεις μπορεί να συσχετίσει με τις δικές του.Αν μου προσδιορίσει ο ερωτών τον παρατηρητή π.χ. ακίνητο ως προς το κέντρο του ήλιου θα μπορούσα να δώσω και μερικές ενδεικτικές εξισώσεις για την Ιδιοπεριστροφή της γύρω από το κέντρο μάζας της και της ελλειπτικής περιφοράς του κέντρου μάζας της Γής γύρω από το κέντρο του Ήλιου με περίοδο περίπου 365,25 ημερών ( Επικαλέστηκα την κίνηση που παρατηρεί παρατηρητής στο κέντρο μάζας της Γης του οποίου γνωρίζω την κίνηση ως προς εμένα -και αγνοώντας τον κλονισμό του άξονα και μεταπτώσεις του – Η κίνηση δεν είναι σύνθετή αλλά η περιγραφή της είναι επαλληλία μαθηματικών εξισώσεων)
Δεν αρνούμαι την αξία του εκπαιδευτικού σχήματος “σύνθετη κίνηση” . Απλά προσπαθώ να προφυλαχτώ από διατυπώσεις που θεωρώ ανόητες και επικίνδυνες π.χ. του τύπου “κάθε σημείο της γής μεταφέρεται με ταχύτητα ίση με την u(cm) και περιστρέφεται με ω” … ¨ ( Πρόσφατα την συνάντησα σε ερώτηση Σωστού-Λάθους ,,, Τι να απαντήσει ο μαθητής 😉
Καλό βράδυ
-
Καλό βράδυ Μήτσο.
Ναι κάθε παρατηρητής βλέπει μια μοναδική κίνηση.
Η μελέτη που κάνει απλουστεύεται (κάποιες φορές) αν χρησιμοποιήσει άλλον παρατηρητή και κάνει αναγωγή.Ο Διονύσης στο παρόν πόνημα υιοθετεί μια Καρτεσιανή λογική.
Περιγραφή με συντεταγμένες. -
Καλημέρα σε όλους και καλή Κυριακή.
Μήτσο, Αποστόλη, Γιάννη και Παντελή σας ευχαριστώ για το σχολιασμό.
Μήτσο η επίκληση της αρχής της επαλληλίας ή ανεξαρτησίας των κινήσεων” έγινε για να είναι συμβατή η λύση, με ό,τι διδάσκεται σήμερα στο σχολείο.
Όμως στην πραγματικότητα χρησιμοποίησα την διανυσματικότητα των μεγεθών μετατόπιση, ταχύτητα, επιτάχυνση και απλά ανάλυσα τα διανύσματα σε εναλλακτικούς ορθογώνιους άξονες x,y και πήρα επαλληλία εξισώσεων κίνησης! Είναι αυτό που ο Γιάννης ανέφερε σαν “Καρτεσιανή λογική”.
Η αντιμετώπιση μέσω παρατηρητών προσλαμβάνεται ευκολότερα από έναν μαθητή, αλλά δεν …μας επιτρέπεται. -
Διονύση καλημέρα.
Στο τελευταίο σχόλιό σου σωστά επισημαίνεις ότι “Όμως στην πραγματικότητα χρησιμοποίησα την διανυσματικότητα των μεγεθών μετατόπιση, ταχύτητα, επιτάχυνση και απλά ανάλυσα τα διανύσματα σε εναλλακτικούς ορθογώνιους άξονες x,y και πήρα επαλληλία εξισώσεων κίνησης!” Αυτό ακριβώς κάνουμε και στη συνηθισμένη περίπτωση που επιλέγουμε τους άξονες κατά μήκος της κίνησης του σώματος, πάνω στο πλάγιο επίπεδο, και κάθετα σε αυτό. Δηλαδή και σε αυτή την περίπτωση μπορούμε να πούμε ότι εφαρμόζουμε την αρχή επαλληλία των κινήσεων μόνο που στον κάθετο άξονα η “κίνηση” είναι τετριμμένη, διότι η μετατόπιση του σώματος σε αυτό τον άξονα είναι μηδενική.
-
Καλημέρα Ανδρέα.
Έτσι είναι, όπως το λες.
Και η καθημερινή αντιμετώπιση με πλάγιους άξονες, την ίδια λογική ακολουθεί. -
Καλησπέρα Διονύση. Ωραία εργασία. Έχουμε δύο ανεξάρτητες κινήσεις και τη σύνθεσή τους. Στα βιβλία μου των Halliday, Serway και Young στην οριζόντια βολή αναφέρουν: combination ή independent. Η έννοια superposition(υπέρθεση, επαλληλία) αναφέρεται αποκλειστικά σε δυνάμεις, ροπές, κύματα και στην ένταση και το δυναμικό ηλεκτρικού πεδίου. Ίσως αν λέγαμε σύνθεση εξισώσεων να ήταν πιο ακριβής, αλλά λιγότερο διδακτική προσέγγιση. Στους μαθητές παρουσιάζεται πιο εύκολα μέσω δύο κινήσεων.
Τι σημαίνει πραγματικά η «Αρχή Ανεξαρτησίας», π.χ. στην οριζόντια βολή;
Φυσικό φαινόμενο: Υπάρχει μία μόνο κίνηση, η παραβολική.
Μαθηματική μελέτη: Λέμε ότι μπορούμε να την “αποσυνθέσουμε” σε δύο απλούστερες κινήσεις, οι οποίες εξελίσσονται ανεξάρτητα (μία στον άξονα x και μία στον άξονα y). Εμείς συνθέτουμε τις εξισώσεις των δύο κινήσεων για να περιγράψουμε την ενιαία φυσική κίνηση.
Άρα η αρχή της επαλληλίας κινήσεων είναι εργαλείο περιγραφής, όχι κυριολεκτική ύπαρξη δύο κινήσεων. -
Καλό απόγευμα Ανδρέα και Γιώργο, σας ευχαριστώ για το σχολιασμό και την κατάθεση της γνώμη σας.
Γιώργο το ερώτημα που βάζεις είναι έτσι και αλλιώς ενδιαφέρον και “στέκει” και σαν ανεξάρτητο θέμα στο φόρουμ.
Αλλά προφανώς δεν ενοχλει και η εδώ παρουσία του.
Και μια απάντηση. Σωστό το γ). -
Καλησπέρα.
Διονύση θέλω να πιστεύω ότι ο Θωμάς διαβάζοντας την
όχι δεν είναι οριζόντια βολή
και την παραπάνω δεν είναι πλέον άπιστος και θα μπορεί να απαντήσει στην
https://i.ibb.co/4ZMQ01F0/2025-10-20-162422.png
Αν νομίζεις ότι δεν είναι εδώ η σωστή θέση μπορείς να την βάλεις στο φόρουμ -
Είναι σαφές ότι πολύ συχνά ο Διονύσης … ιντριγκάρει όλους εδώ και πολύ συχνά μάλιστα (και όχι άδικα) τους …πείθει! Κάτι αντιπαραθετικό προσπάθησε να πει ο Παντελεήμων αλλά κατέληξε στο .. γιατί όχι! Καταλάγιασαν κάπως έτσι τα σχόλια στην παρούσα ανάρτηση (συγχωρέστε με σήμερα μόλις είδα την ανάρτηση, την προτεινόμενη λύση, τα σχόλια). Να πω κι εγώ μια γνώμη τώρα που μου ήρθε ή άργησα; Ένα σχόλιο; Θα πω! (με βάση αυτά που έχω καταλάβει ως δάσκαλος της τάξης ως τώρα)
Α. Ένας παρατηρητής δεν συνηθίζει και δεν χρειάζεται να δανείζεται δεδομένα από άλλους παρατηρητές! Προσπαθεί να εξηγήσει το φαινόμενο που παρατηρεί και για το οποίο πραγματοποιεί, καταγράφει μετρήσεις κ.λ.π. από τις οποίες συμπεραίνει, εξηγεί εν τέλει το φαινόμενο.
Ο παρατηρητής λοιπόν της 2ης απάντησης παρατηρεί ένα σώμα που αφήνεται (ακίνητο) αρχικά πάνω σε ένα πλάγιο επίπεδο, το οποίο στη συνέχεια (για κάποιο λόγο !) κινείται κατά μήκος του (αυτό το δεδομένο έχει, δεν πάει αυτό να αποδείξει- εκεί νομίζω βρίσκεται μια ντρίπλα στην προτεινόμενη λύση και ένα σχετικό «δάνειο» από άλλον παρατηρητή). Ο παρατηρητής προσπαθεί να προσδιορίσει λοιπόν το λόγο που αυτό συμβαίνει με βάση τους νόμους της φυσικής και την έκβασή του στο χώρο και το χρόνο (και το …βαφτίζει στη συνέχεια)!
Επειδή μπορεί να διαλέξει όποιο σύστημα αναφοράς αυτός θέλει, αποφασίζει έστω, για να ξεφύγει από το σύνηθες που του «επιβάλει» ο καθηγητής στο σχολείο και επιλέγει αυτό με οριζόντιο και κατακόρυφο άξονα (Καρτεσιανό το είπατε εδώ, αλλά τα άλλα αντίστοιχα, δεν είναι Καρτεσιανά;). Να σημειώσω εδώ ότι και με το σύνηθες σύστημα αναφοράς να πάει, ίδιο δεν είναι το πρόβλημα του; Δηλαδή να εξηγήσει την παρατηρούμενη κίνηση του σώματος πάνω στο πλάγιο επίπεδο και να προβλέψει το «μέλλον» της;
Παρένθεση εδώ: Μπορεί στο μεταξύ να του περνάνε κι άλλα ερωτήματα από το μυαλό, όπως «γιατί πρέπει το σώμα σώνει και ντε να ακουμπάει στο πλάγιο επίπεδο;» που προφανώς τα απαντάει καθησυχάζοντας τον εαυτό του, « λόγω βάρους»- και ανυπαρξίας άλλης δύναμης που θα το εξέτρεπε προς κάπου προς τα «πάνω» αν κατάφερνε αυτή η άλλη δύναμη, να υπερνικήσει το βάρος! Αναγνωρίζει δηλαδή έτσι κι αλλιώς ότι το σώμα είναι υποχρεωμένο λόγω των συνθηκών (αρχική ακινησία και επίδραση του βάρους) να κινηθεί τουλάχιστον αρχικά σε επαφή με το προσφερόμενο δάπεδο-πλάγιο επίπεδο. Μια άλλη σκέψη του είναι «ναι θα κινηθεί αρχικά σε επαφή με το δάπεδο, μήπως αργότερα τη χάσει αυτή την επαφή και τότε πάει για βολή;» Τι όμως μπορεί να τον βοηθήσει να το διαπιστώσει αυτό; Μα, ο «μαρτυριάρης», ο «ρουφιάνος» των επαφών, η δύναμη επαφής με το λείο δάπεδο, η Ν, ποιος άλλος; Όσο η Ν έχει τιμή διαφορετική από μηδέν, επαφή υπάρχει! Επομένως αυτήν πρέπει να υπολογίσει και από την σταθερή ή μεταβλητή τιμή της να συμπεράνει την επαφή ή το χάσιμό της (οπότε βολή εδώ). Κλείνει η παρένθεση.
Παρατηρεί ότι στο σώμα ασκούνται δύο δυνάμεις Β και Ν (εφόσον δέχεται την συνεχή επαφή του σώματος με το πλάγιο δάπεδο για όσο αυτή υπάρχει). Τη μια τη γνωρίζει, την άλλη όχι αλλά, δεν την δανείζεται! Άρα στόχος του είναι να την υπολογίσει! Αν βρει την τιμή της Ν για την οποιαδήποτε τυχαία θέση, μπορεί και να αποδείξει ότι το σώμα κρατάει την επαφή με το δάπεδο, οπότε σιγουρεύει και ότι δεν πρόκειται για … βολή! Απαντάει έτσι και στον Θωμά! (Αληθινός είναι αυτός; Αν ναι έχει ενδιαφέρον!)
Στη συνέχεια κατά τα γνωστά αναλύει την Ν (αυτή θέλει ανάλυση ενώ η άλλη βρίσκεται στους άξονες) και μετά κάνει όσα ο Διονύσης γράφει (χωρίς όμως τις δανικές αντικαταστάσεις της Ν με Βσυνφ). Η σιγουριά του είναι ότι το σώμα κινείται κατά μήκος του πλάγιου επιπέδου και τριγωνομετρικά το στηρίζει με ημίτονα συνημίτονα ή/και με Π.Θ για να συσχετίσει το χ με το ψ κάθε στιγμή.
Έτσι μέχρι μια τυχαία θέση (με βάση το σύστημα εξισώσεων του Διονύση) και άγνωστη τη Ν την υπολογίζει τόση, όση και ως προς οποιοδήποτε άλλο (από τα συνήθη) σύστημα αναφοράς, δηλαδή Ν=Βσυνφ σταθερή και διάφορη του μηδενός και αντίο βολή!Β. Σε ένα σημείο της συζήτησης ο Ανδρέας θέτει το ερώτημα: Τι σημαίνει πραγματικά η «Αρχή Ανεξαρτησίας», π.χ. στην οριζόντια βολή; και το απαντάει επιχειρηματολογώντας. Λέει: «Φυσικό φαινόμενο: Υπάρχει μία μόνο κίνηση, η παραβολική.»
Δηλαδή το κάθε φυσικό φαινόμενο ορίζεται εκ θεού μονοσήμαντα- αντικειμενικά, απόλυτα; Φοβάμαι ότι αν είναι έτσι, η σχετικότητα της κίνησης και ότι αυτή συνεπάγεται, είναι νοσηρό αποκύημα της αμαρτωλής ανθρώπινης φαντασίας.
Ας δούμε και ας συζητήσουμε λοιπόν τη λεγόμενη οριζόντια βολή: Υπάρχει λέτε (επειδή δεν είδα να παίρνετε θέση να υποθέσω ότι συμφωνήσατε;) μία και μόνο επώνυμη κίνηση που περιγράφει το φαινόμενο αυτό; (ας πούμε η παραβολική;)
1. Για τον (γνωστό αγαπημένο όλων!) παρατηρητή που δεν εννοεί να ξεκολλήσει από τη Γη και εννοεί να είναι καρφωμένος σε ένα σημείο της (σημείο αναφοράς), έχοντας απλώσει τις μεζούρες του (τους άξονες του συστήματος αναφοράς του) βεβαίως τελικά , η παραβολική. Πώς καταλήγει όμως να την βαφτίζει έτσι; Προφανώς αρχικά αναγνωρίζει ότι το σώμα (την κίνηση του οποίου παρατηρεί) και απομακρύνεται π.χ. από τον τοίχο της πολυκατοικίας από την ταράτσα της οποίας έγινε η βολή (και αναρωτιέται πόσο είναι αυτό το «πόσο απομακρύνεται») και βλέπει ότι πλησιάζει το σώμα ολοένα προς τη γη και αναρωτιέται πόσο πέφτει και από τι εξαρτάται αυτό το «πόσο πέφτει» από το αρχικό ύψος. Διαπιστώνει επομένως ή όχι, κυριολεκτική ύπαρξη δύο ταυτόχρονων κινήσεων; Χρειάζεται να έχει διδαχθεί ανεξαρτησία κινήσεων για να το σκεφτεί αυτό, να διαβάσει ευαγγέλια τύπου Halliday, Serway και Young για να προσπαθήσει τελικά να το αποδελτιώσει; Δεν νομίζω! Απεναντίας είναι λογικό ότι θα καταλήξει (αφού με μετρήσεις –και όχι μόνο, δες παρακάτω-το διπλοτριπλοτσεκάρει!) ότι μπορεί αυτό και πολλά άλλα φαινόμενα να τα βλέπει έτσι «συνθετικά» (ανακαλύπτει θέλοντας και μη θέλοντας δηλαδή την «αρχή ανεξαρτησίας» που θα του αποδείξει και την παραβολικότητα!) και με πολύ σιγουριά στη συνέχεια να καταλήγει σε νόμους που του δίνουν δυνατότητα πρόβλεψης-«βάσιμης προφητείας» για την υπό όποιους όρους έκβασή τους.
2. Στο γνωστό πρόβλημα με το αεροπλάνο που αφήνει τη βόμβα, ο πιλότος ως παρατηρητής, προφανώς έχει άλλη γνώμη για την κίνηση της βόμβας. Ελεύθερη κατακόρυφη πτώση χωρίς αρχική ταχύτητα, λέει και την βαφτίζει έτσι.
3. Για έναν τρίτο παρατηρητή που μπορεί να παρατηρεί μόνο παράλληλα στο κατακόρυφο επίπεδο της τροχιάς της βόμβας και στέκεται μετά το σημείο που αυτή φτάνει στο έδαφος; Ελεύθερη κατακόρυφη πτώση χωρίς αρχική ταχύτητα! Συμφωνεί με τον προηγούμενο στην ονοματοδοσία
4. Για έναν τέταρτο παρατηρητή που μπορεί να παρατηρεί μόνο παράλληλα στο επίπεδο της τροχιάς της βόμβας και στέκεται πάνω από την οριζόντια που περνάει από το σημείο βολής; χμμμ μάλλον ευθύγραμμη και ομαλή!
Τα φαινόμενα δεν έχουν όνομα! Ο παρατηρητής τα ονομάζει όπως του …ταιριάζει με βάση την παρατήρησή του!
(θυμήθηκα και την άλλη ερώτηση τώρα με όλη αυτή την παρατηρητηκολογία: «έχουν χρώμα τα σώματα;» χμμμ τον σκύλο να ρωτήσετε!) -
Καλημέρα Αντώνη και σε ευχαριστώ για τον σχολιασμό και την αναλυτική τοποθέτηση.
Όσον αφορά τη συζήτηση για τη μία ή πολλές κινήσεις και τους διάφορους παρατηρητές, να επαναφέρω τμήμα σχολίου μου παραπάνω:
“Η αντιμετώπιση μέσω παρατηρητών προσλαμβάνεται ευκολότερα από έναν μαθητή, αλλά δεν …μας επιτρέπεται.” -
Καλημέρα παιδιά.
Αντώνη ένας παρατηρητής μπορεί να χρησιμοποιήσει καρτεσιανές ή πολικές συντεταγμένες για να περιγράψει μία επίπεδη κίνηση.
Η λογική είναι Καρτεσιανή αν πούμε ότι «Το κινητό κάνει δύο κινήσεις διότι έχει δυο βαθμούς ελευθερίας» ή ότι «Το κινητό κάνει δύο κινήσεις διότι με δύο συντεταγμένες βρίσκουμε τη θέση του».
Προτιμώ το «κάνει δύο κινήσεις» ως περίφραση.
Ο παρατηρητής Α βλέπει τον Β και όχι το κινητό να εκτελεί μία κίνηση και ο Β βλέπει το κινητό να εκτελεί μία άλλη κίνηση.
Παράδειγμα:
https://i.ibb.co/rGymthGJ/Screenshot-1.pngΟ κύριος βλέπει το αγοράκι να κινείται προς τα δεξιά με κάποια ταχύτητα και το αγοράκι βλέπει την μικρά να κινείται προς τα αριστερά με μια ταχύτητα.
Λέμε τότε ότι η μικρά «κάνει δύο κινήσεις». Σε εισαγωγικά. Κινείται σε κινούμενο όχημα. Κάνει ταυτόχρονα την κίνηση του οχήματος και την ως προς το όχημα δική της κίνηση.
Εδώ δεν έχουμε δύο βαθμούς ελευθερίας. -
Διαφωνώ με τη φράση σου:
Ένας παρατηρητής δεν συνηθίζει και δεν χρειάζεται να δανείζεται δεδομένα από άλλους παρατηρητές!
Ιδίως για το “δεν χρειάζεται”.
Μπορεί να μην το κάνει αλλά πολλές φορές εξυπηρετεί αφάνταστα να το κάνει.
Λύνει το πρόβλημα πολύ πιο εύκολα.
Παράδειγμα:
Πόσο έργο παρήγαγε το χέρι;
-
Ευχαριστώ Γιάννης Κυριακόπουλος για τα σχόλιά σου. Βοήθησέ με όμως σε παρακαλώ να καταλάβω σε τι ακριβώς με βοηθούν (να καταλάβω). Ότι μπορούν να συνεννοηθούν μεταξύ τους διαφορετικοί παρατηρητές; Δεν τέθηκε τέτοιο ζήτημα αλλά αν χρειάζεται οπωσδήποτε- εγώ λέω όχι. Το αν επιτρέπεται η επίκληση συμπερασμάτων άλλου παρατηρητή; Προφανώς δεν συγχωρείται αγνωστικισμός στα καθ ημάς και επομένως μπορεί. Αν είναι χρήσιμο; Φυσικά και είναι. Επίσης με το “Παράδειγμα: Πόσο έργο παρήγαγε το χέρι;” τι να καταλάβω; Ότι σώνει και ντε πρέπει να γίνει χρήση συμπερασμάτων; ότι δεν γίνεται αλλιώς;
Προφανώς θέλω να πω ότι άλλη τοποθέτηση έκανα εγώ σε σχέση με το τι είναι και τι χρησιμοποιεί ένας παρατηρητής πρωτόλεια για να βγάλει συμπεράσματα και νόμους αφ εαυτού (και μάλιστα αν μπορεί-εγώ λέω μπορεί) και σε άλλα αναφέρονται τα σχόλια.
Σε σχέση με το “επίδικο” της ανάρτησης στην οποία αναφερόμαστε (2η απάντηση) σχολίασα (όπως σχολίασα) αυτά που διατείνομαι- έχω καταλήξει και επομένως θα περίμενα σχολιασμό επ αυτών. Θα με βοηθούσε εμένα και πιθανά κι άλλους.
Υπάρχει βέβαια και σοβαρή πιθανότητα να μην έχω καταλάβει εγώ τίποτα από όσα παράθεσα στα δικά μου σχόλια (που αν βοηθηθώ θα καταλήξω σε σωστή άποψη και μαζί με εμένα και ο …Θωμάς!).
Γι αυτό υπάρχει το forum. Φαντάζομαι! -
Καλημέρα Αντώνη.
Σχολίασα δύο φράσεις σου:
(Καρτεσιανό το είπατε εδώ, αλλά τα άλλα αντίστοιχα, δεν είναι Καρτεσιανά;).και
Ένας παρατηρητής δεν συνηθίζει και δεν χρειάζεται να δανείζεται δεδομένα από άλλους παρατηρητές!Το πρώτο μου σχόλιο διευκρινίζει τι εννοούσα με το “Καρτεσιανή λογική”.
Το δεύτερο λέει απλά ότι πολλές φορές ο συγκερασμός συμπερασμάτων διαφορετικών παρατηρητών διευκολύνει την επίλυση προβλημάτων.Τίποτα δεν γίνεται “ντε και καλά” , υποχρεωτικά κ.λ.π. Κάθε δρόμος επίλυσης είναι προαιρετικός και θέμα επιλογής. Χρησιμοποιώ τις αδρανειακές δυνάμεις αλλά δεν θα σου επιβάλλω τη χρήση τους.
Κάποια φορά πρέπει να ξανασυζητήσουμε και το τι σημαίνει “κάνει δύο κινήσεις” και τα περί “Αρχής Ανεξαρτησίας κινήσεων” μια και δεν καταλήξαμε τότε και εννοούμε διαφορετικά πράγματα επικαλούμενοι τους όρους αυτούς.
Κάποιοι μιλούν για περιγραφή με δύο συντεταγμένες (και δύο εξισώσεις, μία για κάθε συντεταγμένη).
Άλλοι για κίνηση επί κινούμενου οχήματος ή για παρατηρητές.
Άλλοι μιλούν για δυνάμεις που δέχεται διαδοχικά το σώμα, υποτάσσοντας την Κινηματική στη Δυναμική.
Άλλοι ανάγουν το θέμα στην γραμμικότητα ή όχι των διαφορικών εξισώσεων που σχετίζονται με το πρόβλημα.
Άλλοι στην Γεωμετρία του χώρου (επίπεδο ή γήινη επιφάνεια;).
Δεν έχουμε καταλήξει κάπου και διαφωνίες εμφανίζονται όταν εννοούμε άλλο πράγμα ο καθένας.Ναι και γι’ αυτό υπάρχει το φόρουμ. Κυρίως είναι ένα διαδικτυακό καφενείο που φέρνει σε επαφή ανθρώπους. Αν ωφεληθούν κιόλας ακόμα καλύτερα.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 μήνα
Ένα παράδοξο ζητάει εξήγηση.
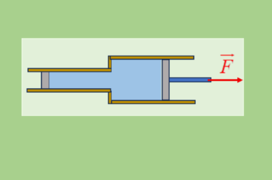 Το αριστερό έμβολο έχει διατομή Α και το δεξί 2Α. Θέλουμε να κινείται το δεξί με σταθερή ταχύτητα υ και φυσικά λόγω συνέχειας το αριστερό με ταχύτητα 2υ. Ποια δύναμη πρέπει να ασκούμε στο δεξί έμβολο; Συνέχεια:
Το αριστερό έμβολο έχει διατομή Α και το δεξί 2Α. Θέλουμε να κινείται το δεξί με σταθερή ταχύτητα υ και φυσικά λόγω συνέχειας το αριστερό με ταχύτητα 2υ. Ποια δύναμη πρέπει να ασκούμε στο δεξί έμβολο; Συνέχεια:-
Καλησπέρα Γιάννη. Μήπως η δυναμη πρέπει να ασκηθεί στο μικρό εμβολο;. Ετσι δικαιολογείται η κινηση. Με τον τροπο που περιγράφεις φαίνεται ότι το υγρό δεν προλαβαίνει να ακολουθήσει το εμβολο. Δημιουργείται υποπίεση πισω από ο μεγάλλο έμβολο και στατική και δυναμική
-
Καλησπέρα Διονύση και Γιώργο.
Διονύση τι εννοείς με το “ενέργεια πίεσης”;
Το γινόμενο P.V ;Γιώργο το παράδοξο ισχύει και όταν η δύναμη ασκείται στο μικρό:
https://i.ibb.co/xK4CW3wG/Screenshot-1.png -
Το εργο της F δεν είναι το αθροισμα των κινητικών ενεργειών και οχι η διαφορά τους;
-
Όχι το έργο της F στο χρονικό διάστημα Δt είναι ίσο με τη μεταβολή της συνολικής ενέργειας του συστήματος στο ίδιο χρονικό διάστημα.
Το παρόν κείμενο ισχυρίζεται ότι η δυναμική ενέργεια μένει σταθερή και ότι η κινητική ενέργεια μειώνεται. -
Δεν ασχολούμαι με το έργο που παράχτηκε μέχρι το σύστημα να τεθεί στην κατάσταση που περιγράφεται, ούτε με την αρχική δύναμη.
Κάποια στιγμή t1 οι ταχύτητες είναι αυτές. Ποιο το έργο της δύναμης από τη στιγμή t1 ως νια μεταγενέστερη στιγμή t2 ;
Αν η ενέργεια μειώνεται τότε το έργο από t1 ως t2 είναι αρνητικό. -
Μα η μεταβολή της κινητικής ενέργειας μεταξύ ηρεμίας και καποιας επόμενης χρονικής στιγμής του συστήματος είναι :
ΔΚ= (1/2) Δm * υ^2 + (1/2) Δm (2υ)^2
Και αυτή ίση με το έργο της F
Όσο ασκείται η F ( απουσία αλλων εξωτερικών δυνάμεων) , τοσο αυξάνεται η ταχύτητα του συτήματος (η οποια δεν μένει σταθερή). -
Ναι είναι (υποτίθεται φυσικά) το έργο από την αρχή του φαινομένου ως κάποια στιγμή.
Έργο με το οποίο δεν ασχολήθηκα.
Δεν με απασχόλησε πόσο έργο δαπανήσαμε για να πετύχουμε την αρχική κατάσταση, έργο που είναι μεγάλο αν τα νερά στους σωλήνες είναι 100 κιλά το καθένα.
Το παράξαμε με κάποιο τρόπο και στη συνέχεια θέλουμε αυτές τις σταθερές ταχύτητες.
Πόσο έργο παράγουμε από τη σταθεροποίηση και μετά;
Λέω ότι αν ένα κιλό νερό μπει από αριστερά (ταχύτητα 2) στα δεξιά (ταχύτητα 1) έχω (υποτίθεται) μεταβολή κινητικής ενέργειας:
1/21.1-1/21.4=-1,5J. -
Ναι Διονύση αυτό λέω.
Τη σημειώνω προς τα δεξιά και τη βγάζω αρνητική. Δηλαδή σπρώχνει και δεν τραβά.
Όμως ισχύει ο νόμος Μπερνούλι όπως γράφτηκε; -
Αρα η μεταβολή της Κ.Ε που παιρνεις δεν παιζει με τις εξωτερικές δυνάμεις!
-
Παίζει Γιώργο με τις εξωτερικές δυνάμεις.
Έχουμε ένα σύστημα στο οποίο η κινητική ενέργεια μειώνεται (υποτίθεται) με ρυθμό:
https://i.ibb.co/hF4D3C54/Screenshot-1.pngΤη μεταβολή αυτήν την προκαλεί η δράση της εξωτερικής δύναμης.
Εκτός αν….. -
Καλησπέρα Γιώργο.
Αν το υγρό είναι ιδανικό και ισχύει η εξίσωση Bernoulli… -
Καλό απόγευμα Γιάννη.
Στην εξίσωση Bernoulli η κινητική ενέργεια ανά μονάδα όγκου, κατά το πέρασμα από περιοχή μικρής πίεσης (αριστερά) σε περιοχή μεγαλύτερης πίεσης (δεξιά), δεν είναι αυτή που αυξάνει την πίεση; Έτσι δεν διατηρείται η ενέργεια; Από κινητική σε ενέργεια πίεσης; -
Τι εννοώ Γιάννη. Αν πάρουμε δύο σημεία στις δυο περιοχές που δίνεις, στο ίδιο ύψος η εξίσωση Bernoulli δίνει:
https://i.ibb.co/1GGjQFdy/2025-10-16-191818.png
Αν ο ένας προσθετέος μας δίνει την κινητική ενέργεια ανά μονάδα όγκου, ο άλλος δεν πρέπει να δίνει την “ενέργεια ανά μονάδα όγκου” που οφείλεται στην πίεση;
Να το πω αλλιώς;
Ας μετατρέψουμε λίγο την εξίσωση:
https://i.ibb.co/mVbYtvxL/2025-10-16-192837.png
Η μεταβολή της κινητικής ενέργειας συνδέεται με το έργο που παράγει σε μια μάζα m το υπόλοιπο υγρό λόγω διαφοράς πίεσης. Η ΔΚ δεν συνδέεται με το έργο της εξωτερικής δύναμης.
Αλλά και κάτι ακόμη:
Για να έχεις αυξημένη πίεση στο φαρδύ τμήμα, αφού έχεις μικρότερη ταχύτητα ροής, η ασκούμενη εξωτερική δύναμη στο έμβολο είναι αντίθετη αυτής που σημείωσες, για να κινείται με σταθερή ταχύτητα το δεξιό έμβολο. -
Διονύση με μεγάλες διαμέτρους το νερό μπορεί να θεωρηθεί ιδανικό υγρό.
Αν όχι ας μιλήσουμε για ιδανικό υγρό.
Ισχύει η εξίσωση Μπερνούλι;Προφανώς κάνω δύο λάθη (που είναι ένα στην ουσία) και οι δύο αποδείξεις καταλήγουν στα ίδια. Ποιο είναι το λάθος;
-
Και ο Γιάννης Γιώργο, δεν θέλει να μας αφήσει να …ξεχάσουμε τα ρευστά, πάνω που τα …καταφέρναμε 🙂
-
Δεν βλέπω κάτι άλλο Γιάννη, πέρα από το προφανές ότι για να έχεις μεγαλύτερη από την ατμοσφαιρική πίεση στο δεξιό τμήμα, η δύναμη έχει αντίθετη φορά από αυτήν που σημείωσες στο σχήμα.
Αν ήταν έτσι η δύναμη τότε η πίεση πίσω από το έμβολο είναι μικρότερη από την ατμοσφαιρική. -
Διονύση για να εφαρμόσουμε τη σχέση Μπερνούλι πρέπει να έχουμε στρωματική ροή.
Έχουμε όμως;
https://i.ibb.co/sJwmrC2T/Screenshot-1.pngΗ μάζα που μπαίνει έχει ίδια ταχύτητα με τα στρώματα που την περιβάλλουν;
Μειώθηκε η κινητική ενέργεια ή έχουμε στον δεξιό σωλήνα μια ανοργάνωτη κινητική ενέργεια που θα παραμείνει (ιδανικό υγρό) ή θα γίνει θερμότητα (πραγματικό υγρό); -
Δίκιο έχεις Γιάννη!!!
Ναι, την έχασε την ενέργεια η μάζα και δεν το πήρε και …χαμπάρι!!! Σκόρπισε.
Πάει και η εξίσωση του μακαρίτη!!! -
Καλησπέρα σε όλους.
Γιάννη μας θύμισες τα παλιά. Ήμουν σίγουρος ότι το έχεις ξαναθέσεις το ερώτημα.Να θυμίσω μίά ανάρτηση του Γιάννη
Είναι δυαντόν η ισχύς να είναι μηδενική;
και μία δική μου με αφορμή του Γιάννη όπου αξίζει να διαβάσει κάποιος τα σχόλια του Γιάννη και του Διονύση.
η δύναμη στο έμβολο -
Γεια σου Χρήστο.
Την είχα ξεχάσει.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μήνα
Η ισορροπία ή μη, μιας ράβδου
 Μια ομογενής ράβδος ΑΒ, μήκους L, αφήνεται σε ισορροπήσει σε λείο οριζόντιο επίπεδο, σχηματίζοντας με το επίπεδο γωνία φ, όπου ημφ=0,6 και συνφ=0,8, ενώ […]
Μια ομογενής ράβδος ΑΒ, μήκους L, αφήνεται σε ισορροπήσει σε λείο οριζόντιο επίπεδο, σχηματίζοντας με το επίπεδο γωνία φ, όπου ημφ=0,6 και συνφ=0,8, ενώ […]-
Καλημέρα Διονύση.
Πολύ μου άρεσε αυτό που έστησες!
Να είσαι καλά! -
Καλημέρα Διονύση, θα συμφωνήσω με τον Δημήτρη (καλημέρα Δημήτρη), πολύ ωραία άσκηση.
-
Καλημέρα Δημήτρη, καλημέρα Παύλο.
Χαίρομαι που σας άρεσε … -
Καλό μεσημέρι Κωνσταντίνε και σε ευχαριστώ για την εναλλακτική λύση που ανέβασες.
Στο μεταξύ μου έστειλε μήνυμα και ο Κώστα Ψυλάκος (ευχαριστώ και από εδώ Κώστα), ο οποίος μου επεσήμανε την λάθος αντικατάσταση στο μέτρο της Ν2, οπότε έβγαζα και λάθος συντελεστή οριακής στατικής τριβής.
Διόρθωσα, οπότε επιβεβαιώνεται το αποτέλεσμα που βρήκες και συ. -
Καλημερα Διονυση,Πολυ καλη ασκηση. Το Ερωτημα iii) το λυνω ως εξης: H iσορροπια απαιτει και οι τρεις δυναμεις που ασκουνται στην ραβδο Β,Ν1,F να ειναι παραλληλες μεταξυ τους. Αρα Τ/Ν=εφφ.
https://i.ibb.co/LDPJ6vbc/2025-10-16-124457.png -
Καλημέρα Διονύση. Πολύ καλή. Αυτού του είδους τα θέματα ακονίζουν τη σκέψη, αφού βάζουν το μαθητή σε διαδικασία ελέγχου του αν ικανοποιούνται οι συνθήκες ισορροπίας. Απαραίτητη προϋπόθεση βέβαια, ο σχεδιασμός των δυνάμεων.
-
Γεια σου και παλι Διονυση και σε ολη την παρεα. Η λογικη της ασκησης αν εξαιρεσουμε το ερωτημα i) το οποιο ειναι διαφορετικο,ειναι οτι η ισορροπια επιτυγχανεται εαν και μονον εαν μ μεγαλυτερο ειτε ισον του εφφ.(και το σημειο επαφης ραβδου κιβωτιου να μην ειναι αριστερα του μεσου) Το ερωτημα ιι) κατα την γμωμη μου πρεπει να επεται του ερωτηματος ιιι) του οποιου ειναι μια απλη εφαρμογη. Στην λυση που στελνω φαινεται ποσο ισχυρη αν και πολυ απλη μπορει να ειναι μια μεθοδος (και αυτο πρεπει να μεινει σε εναν μαθητη που παει για Πολυτεχνειο) οπως οτι αν εχουμε δυο παραλληλες δυναμεις και μια τριτη,για να υπαρχει ισορροπια, πρεπει αναγκαστικα και η τριτη να ειναι παραλληλη με τις αλλες δυο.
-
Καλό απόγευμα Αποστόλη.
Σε ευχαριστώ για το σχολιασμό.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 μήνα
Διαδοχικές ανελαστικές κρούσεις.
 Έχουμε δυο κατακόρυφους λείους τοίχους. Έχουν ύψη 80 m και απέχουν 10 m. Από το ψηλότερο σημείο του ενός βάλλεται οριζόντια, όπως στο σχ […]
Έχουμε δυο κατακόρυφους λείους τοίχους. Έχουν ύψη 80 m και απέχουν 10 m. Από το ψηλότερο σημείο του ενός βάλλεται οριζόντια, όπως στο σχ […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μήνα
Σαν σκηνές από ταινία προσεχώς…
 Ένα μικρό σώμα Σ εκτελεί ομαλή κυκλική κίνηση σε οριζόντιο επίπεδο, δεμένο στο άκρο μη εκτατού νήματος μήκους l=R=(8/π)=2,5m, με ταχύτητα μέτρου υ=2m/s […]
Ένα μικρό σώμα Σ εκτελεί ομαλή κυκλική κίνηση σε οριζόντιο επίπεδο, δεμένο στο άκρο μη εκτατού νήματος μήκους l=R=(8/π)=2,5m, με ταχύτητα μέτρου υ=2m/s […]-
Καλημέρα Διονύση.
Ωραίος ο τίτλος και το θέμα βεβαίως !
Όπως ακριβώς το έχεις σε μια διδακτική ώρα,
φέρνεις τον Β΄ετή, μια τάξη ψηλότερα χωρίς ιδιαίτερη δυσκολία.
Καλή εβδομάδα -
Καλημέρα Παντελή και σε ευχαριστώ για το σχόλιο.
Επειδή οι μαθητές της Β΄ βιάζονται να αρχίσουν την προετοιμασάι για τις πανελλαδικές και οι πληροφορίες λένε ότι κάπου εκεί στα Χριστούγεννα, εγκαταλείπουν την ύλη της Β΄ και αρχίζουν την αντίστοιχη της Γ΄, είπα να τους δώσω ένα παράδειγμα, όπου μαθαίνοντας καλά την κυκλική κίνηση, εύκολα οδηγούνται και στην μελέτη μιας ταλάντωσης… -
Καλημέρα παιδιά. Διονύση μάλλον δύσκολο να κάνει ο σημερινός μαθητής το συνειρμό για τις Νταλίκες, αλλά θα ωφεληθεί σίγουρα από τη σύνδεση των δύο κινήσεων.
-
Γεια σου Αποστόλη.
Και η Αθήνα μια μητρόπολη του νότου… -
Καλησπέρα Διονύση. Ωραίο θέμα και μια ενδιαφέρουσα ανάλυση της ομαλής κυκλικής κίνησης. Αντιστρέφοντας το συλλογισμό σου, με την ΑΑΚ στην ύλη, μπορούμε να δείξουμε σε έναν μαθητή ότι όπως μελετάμε την οριζόντια βολή έτσι μπορούμε και την ΟΚΚ. Η σύνθεση των δύο εξισώσεων δίνει ουσιαστικά της εξίσωση κυκλικής τροχιάς.
Άλλο βέβαια τι μπορούμε και άλλο τι κάνουμε…σε 8 ώρες Καμπυλόγραμμες.
Και για να μην έχεις αγωνία, μετά τη χαμένη διδακτικά “Ημέρα Αθλητισμού, έρχεται η επίσης χαμένη διδακτικά “Ημέρα Ψυχικής Υγιεινής” και ακολουθούν αμέτρητες “Ημέρες”. Η εβδομάδα έχει τέσσερις διδακτικές ημέρες στην καλύτερη περίπτωση. -
Καλημέρα Ανδρέα και σε ευχαριστώ για το σχολιασμό.
Το συμπέρασμα που λες, ότι όπως μπορούμε να αναλύσουμε την οριζόντια βολή παίρνοντας επαλληλία δύο εξισώσεων κίνησης, μια για κάθε άξονα (x,y), το ίδιο μπορούμε να κάνουμε και για την κυκλική κίνηση. Νομίζω ότι το συμπέρασμα βγαίνει αυτόματα, από την παραπάνω ανάρτηση…
Αλλά προτίμησα να μην το επισημάνω, αφού “δεν υπάρχει” και η “αντίστροφη πορεία”! Η “αναπλαισίωση” εξαφάνισε την σύνθεση ταλαντώσεων…
Άντε να πεις τώρα ότι η σύνθεση δύο κάθετων αρμονικών ταλαντώσεων ίδιας συχνότητας και ίδιου πλάτους οδηγεί σε κυκλική κίνηση!!!!
Αυτό και αν είναι θανάσιμο αμάρτημα!!!
ΥΓ
Μου αρέσει να μαθαίνω λέξεις σύγχρονες… 🙂
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μήνα
Μια σύνθετη κίνηση ράβδου
 Μια ομογενής ράβδος μήκους 2m κινείται οριζόντια, σε λείο οριζόντιο επίπεδο και στο σχήμα φαίνεται η θέση της ράβδου, τη στιγμή t0=0, όπου το μέσον της […]
Μια ομογενής ράβδος μήκους 2m κινείται οριζόντια, σε λείο οριζόντιο επίπεδο και στο σχήμα φαίνεται η θέση της ράβδου, τη στιγμή t0=0, όπου το μέσον της […]-
Αφιερωμένη στον Θοδωρή Παπασγουρίδη.
Όταν η εικόνα μιας στιγμής, γίνεται κίνηση για χρονικό διάστημα 2s. -
Γειά σου Διονύση.
Υψηλότατου επιπέδου σενάριο κατά τη γνώμη μου και η λύση να απαιτεί ψυχραιμία, υπομονή και βηματισμό συντονισμένο στα ερωτήματα!
Να είσαι καλά -
Πολύ ωραία άσκηση Διονύση που έχει «διάρκεια» στην μελέτη της κίνησης και ξεφεύγει από την ενασχόληση με μια χρονική στιγμή του φαινομένου.
-
Καλημέρα σε όλους, ευχαριστώ Διονύση για την ανάρτηση και τον χρόνο που αφιέρωσες. Την είδα “διαγώνια”, θα την δω μέσα στην μέρα πιο προσεχτικά και θα επανέλθω. Μία φράση, με προβληματίζει…
-
Διονύση, καλημέρα.
Πιο όμορφη και πιο δύσκολη από την προηγούμενη, αν και στο ίδιο μοτίβο.
Ο υπαινιγμός σου ότι η περιγραφή της μεταφορικής κίνησης μπορεί να γίνει με επιλογή οποιουδήποτε σημείου της ράβδου (ή σημείου άσχετου με τη ράβδο) και ότι τα υπόλοιπα σημεία εκτελούν κυκλικές κινήσεις γύρω απ’ αυτό, πως μπορεί να γίνει αποδεκτός αν δεν έχει θεμελιωθεί μαθηματικά; Οι μαθητές έχουν το κέντρο μάζας ως τέτοιο που βολεύει στη δυναμική της κίνησης, αλλά στην κινηματική της είναι ισότιμο με τα υπόλοιπα.
Να ‘σαι καλά. -
Πολύ καλή Διονύση!
-
Καλημέρα Ντίνο.
Έχεις απαντήσει ο ίδιος σε σχόλιό σου σε άλλη συζήτηση:
-Σχετική ταχύτητα. -
Καλημέρα συνάδελφοι.
Παντελή, Παύλο, Θοδωρή, Ντίνο και Γιάννη σας ευχαριστώ για το σχολιασμό.
Ντίνο, ο “υπαινιγμός” έγινε επειδή δεν είναι προς χρήση από μαθητές, αλλά για μυημένους…
Οι μαθητές διδάσκονται την περιστροφή γύρω από το cm και αυτό έκανα και παραπάνω στην απάντηση… -
Καλημέρα σε όλους. Διδακτικότατη Διονύση!
-
Ευχαριστώ Αποστόλη.
-
Kαλησπερα Διονυση,και σε ολη την παρέα.Πριν πω οτιδηποτε εχω να πω οτι η ασκηση ειναι πολυ δυσκολη αλλα και πολυ ωραια ομως.Υπαρχουν διαφορετικα σεναρια με το ιδιο στιγμιοτυπο που δινεις την στιγμη μηδεν.
Η κινηση της ραβδου μπορει να θεωρηθει μεταφορικη κατα μηκος του αξονα y,της οποιας την στιγμη μηδεν ολα τα σημεια της ραβδου εχουν την επιταχυνση που εχει και το σημειο Α και καταλληλη ταχυτητα και ταυτοχρονως στροφικη γυρω απο το Α ,με τετοια γωνιακη επιταχυνση,ωστε το κεντρο Ο να εχει εκτος της επιταχυνσης που εχει και το Α,και μια επιτροχια επιταχυνση αντιθετη αυτης του Α.Ετσι η μονη επιταχυνση που θα εχει το Ο θα ειναι η κεντρομολος ωωR=(5/8)m/ss και η γωνιακη επιταχυνση βγαινει (π/4)rad/ss
Aλλη υλοποιηση με το ιδιο αρχικο στιγμιοτυπο ειναι η ραβδος να κανει στροφικη κινηση γυρω απο το Ο και μεταφορικη κινηση της οποιας την στιγμη μηδεν ολα τα σημεια της ραβδου εχουν την επιταχυνση και την ταχυτητα που εχει και το σημειο Ο, οπως θεωρησες και εσυ,ομως η επιταχυνση του Ο να μην ειναι σταθερη αλλα να ειναι η κεντρομολος επιταχυνση κυκλικης κινησης του Ο σαν να ηταν η ραβδος πανω σε ρόδα του λουνα παρκ. κλπ κλπ.
Ειμαστε ακομα στο ερωτημα i).
Εν συνεχεια παμε στο ερωτημα ii) και ο μαθητης που σκεφτηκε ολα τα προηγουμενα,βλεπει το δεδομενο η επιταχυνση του κεντρου Ο να ειναι σταθερη παθαινει ενα ψυχολογικο σοκ. 🙂
Επισης θα ηθελα να παρατηρησω οτι στα προβληματα αυτου του τυπου,τα οποια ειναι προβληματα Γεωμετριας μετα χρονου οπως λεει και ο φιλος μου Γιαννης,δεν χρειαζεται να μιλαμε για ομογενη ραβδο,κεντρα μαζας δυναμεις κλπ. Στην εκφωνηση πολυ ωραια αναφερεσαι στο μεσον Ο της ραβδου. Γιατι στην λυση του αλλαζεις την ονομασια και το λες κεντρο μαζας; -
Καλησπέρα Κωνσταντίνε και σε ευχαριστώ για την κατάθεση της σκέψης σου.
Η ανάρτηση αυτή έρχεται σαν συνέχεια της προηγούμενης και των σχολίων που ακολούθησαν, πάνω στο ζήτημα για το ποια κίνηση κάνει η ράβδος.
Αποφάσισα λοιπόν να γράψω μια άσκηση που να αναδεικνύει τη θέση μου ( δεν λέω αν είναι εύκολη ή δύσκολη, αλλά μια άσκηση που να μπορεί να αντιμετωπισθεί και από έναν μαθητή).
Άρα πάμε με βάση το τι διδάσκεται ένας μαθητής:
«Η κινηση της ραβδου μπορει να θεωρηθει μεταφορικη κατα μηκος του αξονα y,της οποιας την στιγμη μηδεν ολα τα σημεια της ραβδου εχουν την επιταχυνση που εχει και το σημειο Α»
Αυτό δεν ευσταθεί αφού «μεταφορική σημαίνει όλα τα σημεία να έχουν ίδια ταχύτητα και ίδια επιτάχυνση και στα δεδομένα έχουμε διαφορετικές επιταχύνσεις, αλλά και γωνιακή ταχύτητα!
Στη συνέχεια « και ταυτοχρονως στροφικη γυρω απο το Α, με τετοια γωνιακη επιταχυνση,ωστε το κεντρο Ο να εχει εκτος της επιταχυνσης που εχει και το Α,και μια επιτροχια επιταχυνση αντιθετη αυτης του Α.Ετσι η μονη επιταχυνση που θα εχει το Ο θα ειναι η κεντρομολος ωωR=(5/8)m/ss και η γωνιακη επιταχυνση βγαινει (π/4)rad/ss»
Εδώ δύο πράγματα. Το ταυτόχρονα στροφική σημαίνει όχι μεταφορική αλλά σύνθετη, συνεπώς η προηγούμενη πρότασή σου δεν ευσταθεί.
Αυτή την οπτική γωνία είχε παρουσιάσει δίπλα και ο Γιώργος Χριστόπουλος: «Ουσιαστικά η κίνηση που είπα είναι η κίνηση που θα έβλεπε ένας παρατηρητής στο Α.». Νομίζω οι μαθητές δεν γνωρίζουν τα περί κινούμενου παρατηρητή.
Άρα ο μαθητής έχει να αντιμετωπίσει μια σύνθετη κίνηση. Πώς διδάσκεται στο σχολείο η σύνθετη κίνηση;
Πέρα από το ότι οι υποψήφιοι διδάσκονται σύνθετη κίνηση γύρω από το κέντρο μάζας (γι΄ αυτό στη λύση αντικαθιστώ τη λέξη «μέσον» με το cm», για να είμαι πιο κοντά στη γλώσσα που έχουν καλώς ή κακώς διδαχτεί…), άρα η διαφορετική θεώρηση είναι έξω από την γνωστική περιοχή, δεν συμβιβάζεται με την εκφώνηση που μιλάει για:
«Αν η επιτάχυνση το κέντρου Ο, καθώς και η γωνιακή επιτάχυνση της ράβδου παραμένουν σταθερές, ζητούνται, για τη χρονική στιγμή t1=2s»
Αν η σύνθετη κίνηση δεν γίνεται με περιστροφή γύρω από το μέσον Ο, αλλά γύρω από το άκρο Α, τότε πώς παραμένει διαρκώς σταθερή η επιτάχυνση το Ο; Και η επιτάχυνση του Α τι κάνει (επιτάχυνση η οποία υποτίθεται ότι αποδίδεις στην «μεταφορική κίνηση»; Αλλάζει, μένει σταθερή;
Θεωρώ δηλαδή ότι απλά βάζεις προβλήματα και θεωρήσεις, όπου κανένας μαθητής, με βάση το τι έχει διδαχθεί και το τι καλείται να γνωρίζει για τις εξετάσεις του, δεν θα ασχοληθεί.
Ακόμη όμως και αν πάει να απαντήσει το 1ο ερώτημα χωρίς να έχει διαβάσει τη συνέχεια (για την σταθερή επιτάχυνση του Ο), θα μπορούσε να χρησιμοποιήσει την δική σου θεώρηση. Ας το κάνει. Βέβαια αμέσως μετά στο ερώτημα ii) πρέπει να επιστρέψει σε πιο λογικές εκδοχές…
Αλλά και η 2η εκδοχή που βάζεις «ομως η επιταχυνση του Ο να μην ειναι σταθερη αλλα να ειναι η κεντρομολος επιταχυνση κυκλικης κινησης του Ο σαν να ηταν η ραβδος πανω σε ρόδα του λουνα παρκ. κλπ κλπ.» πάλι έρχεται σε αντίθεση με την σταθερή επιτάχυνση του Ο, της εκφώνησης, οπότε πάμε στα ίδια. Αλλά και αν το σκεφτεί ένας μαθητής; Ας το κάνει… Και πάλι θα υπολογίσει σωστά την επιτάχυνση και τη γωνιακή επιτάχυνση,
Όσο για το τελευταίο μέρος με το cm, απάντησα παραπάνω… -
Διονυση ποτε δεν ειπα οτι η κινηση ειναι μεταφορικη σκετο.Μεταφορικη και ταυτοχρονως στροφικη ειπα δηλαδη Συνδιασμος μεταφορικης κατα μηκος του y και στροφικης γυρω απο το Α ειπα αρα συνθετη. Τι δεν ευσταθει?
Μαλλον δεν καταλαβες τι εχω γραψει ή εγω δεν το εξεφρασα απολυτως σωστα.
Στην συνεχεια γραφεις:
“Αν η σύνθετη κίνηση δεν γίνεται με περιστροφή γύρω από το μέσον Ο, αλλά γύρω από το άκρο Α, τότε πώς παραμένει διαρκώς σταθερή η επιτάχυνση το Ο; ”
Η επιταχυνση του Ο δεν ειναι σταθερη με βαση την εκφωνηση. Αυτο ισχυει για το ερωτημα ii). μονο. Δεν ειναι υποχρεωμενος ο μαθητης να διαβασει το ερωτημα ιι) για να απαντησει το ερωτημα i) Το ερωτημα i) για να απαντηθει χρειαζεται να σκεφτουμε μια υλοποιηση της οποιας το στιγμιοτυπο να ειναι αυτο που βλεπουμε στο σχημα σου και τα σεναρια δεν ειναι μοναδικα,αυτο εξηγω. Ηδη εχουμε περιγραψει τρια διαφορετικα σεναρια. Και η επιταχυνση του Α δεν ειναι υποχρεωτικο να ειναι σταθερη (σαν η ραβδος να επεφτε μεσα στο ομογενες πεδιο βαρυτητας),απλως την στιγμη μηδεν πρεπει να ειναι π/4 και αυτο συνδιαζεται με γωνιακη επιταχυνση π/4 την ιδια χρονικη στιγμη,άρα εχουμε και περισσοτερα σεναρια.
Δεν υπαρχει πιο λογικο και ευλογο σεναριο ,όλα ειναι εξισου λογικα.
Το προηγουμενο προβλημα σε προηγουμενη αναρτηση σου δεν το εχω διαβασει. Αυτο το προβλημα το θεωρω αυτοτελες. -
Κωνσταντίνε, προφανώς διαφωνούμε για τα σενάρια.
Ο μαθητής που τυχόν θα ασχοληθεί, ένα σενάριο έχει διδαχθεί.
Δεν γνωρίζει τη θεωρία, που με αφορμή την παρατήρησή σου, επαναφέρω δίνοντας δύο δικές μου αναρτήσεις:Γιατί το «να κόβεις δρόμο» είναι καλό…
Γιατί το «να κόβεις δρόμο» είναι καλό και για επιταχύνσεις…
Άλλωστε και οι δύο αναρτήσεις αυτές απευθύνονται σε καθηγητές.
Να προσθέσω ακόμη κάτι.
Δίνοντας ότι η ράβδος είναι ομογενής, αυτομάτως το μέσον της Ο, είναι και κέντρο μάζας. Άρα δεν είναι λάθος να το ονομάζω κέντρο μάζας.
Το ότι θα μπορούσα να μην βάλω στη συζήτηση τον όρο “κέντρο μάζας”, ναι θα μπορούσα, αλλά διδακτικά πάντα κάνουμε κάποιες τακτικές υποχωρήσεις, για κάποιο λόγο. Αν λοιπόν αύριο έμπαινα να διδάξω σε μια τάξη, όπου όλοι οι μαθητές έχουν πάει φροντιστήριο και έχουν μάθει να χρησιμοποιούν το cm, το πολύ – πολύ να έκανα μια αναφορά στο σωστό, αλλά δεν θα επέμενα από εκεί και πέρα να επαναλαμβάνω, σε κάθε περίπτωση, την μη απαραίτητη συνθήκη του cm.
Αυτή η επαναλαμβανόμενη επισήμανση, είναι σαν να είμαι υποχρεωμένος κάθε φορά που μπαίνω σε εκκλησία να εκφωνώ το πιστεύω: “πιστεύω σε ένα Θεό…”.
Και ξέρεις αυτό δεν ονομάζεται “πιστεύω”, επισήμως ονομάζεται “ομολογία πίστεως”!!! -
Ψάχνοντας τις δύο παλιότερες αναρτήσεις, του προηγούμενου σχολίου, είδα και κάποια σχόλια.
Μεταφέρω τμήμα σχολίου του αείμνηστου Βαγγέλη Κορφιάτη:
“Βέβαια στην τάξη δεν τολμώ να ξεφύγω από το κέντρο μάζας.
Η οδηγία είναι:
¨όταν υπάρχει φυσικός άξονας περιστροφής (σούβλα ή καρφί ..) η περιστροφή γίνεται ως προς αυτόν. ¨
Όταν ο άξονας περιστροφής είναι νοητός, τότε θεωρούμε ότι διέρχεται από το κέντρο μάζας.
Ακόμη και κινηματικά δεν ξεφεύγω από αυτήν την λογική. Φοβάμαι ότι στην αντίθετη περίπτωση θα γίνει κομφούζιο.” -
Ενταξει δεν υπαρχει λογικο σφαλμα αφου σε ομογενη ραβδο μεσον και κεντρο μαζας ταυτιζονται αλλα σε ασκησεις κινηματικης καλο ειναι μα μην μπαινουμε σε χωραφια δυναμικης. Αυτη ειναι η γνωμη μου τουλαχιστον εις οτι αφορα την κομψοτητα των διατυπωσεων. Στην εκφωνηση σου την οποια θα μπορουσε ενας μαθητης να την διαβασει και κατοπιν να λυσει την ασκηση μονος του χωρις να διαβασει την δικη σου λυση,αναφερεσαι και πολυ σωστα στο μεσον της ραβδου. Δεν υπαρχει κανενας λογος στην συνεχεια να αναφερεσαι στο κεντρο μαζας. Δεν υπαρχει επισης λογος και πουθενα δεν χρειαζεται στην συζητηση που ακολουθει,η ραβδος να ειναι ομογενης.
-
Κωνσταντίνε και ο Διονύσης και όσοι φίλοι αναρτούν υλικό για την τάξη βρίσκονται στη δυσάρεστη θέση να προσαρμοστούν σε μια κακή παρουσίαση ενός θέματος από το σχολικό βιβλίο. Δεν μπορούν να κάνουν διαφορετικά ώστε η άσκηση να είναι νόμιμη.
-
Γιαννη συγνωμη αλλα δεν το καταλαβαινω. Η ραβδος δεν χρειαζεται καν να εχει μαζα μπορει να ειναι μονο μια εικονα τι κεντρο μαζας και νομιμοτητες?
Ειναι σαν να λεμε οτι για να ειναι νομιμη η Γεωμετρια πρεπει τα σχηματα να εχουν μαζα. Ειναι δυνατον να συμφωνησει κανενας με αυτην την ανοησια? -
Διονύση επιστρέφω, έστω και αργοπορημένος…
Με καλύπτει το σχόλιο του Βαγγέλη του Κορφιάτη, το οποίο
συμπληρώνω με την ανάρτησηΓια όποιον βαρεθεί να τη διαβάσει, ας κρατήσει τον επίλογο της άσκησης:
“Για όσο χρόνο υπάρχει άξονας, υποχρεώνεται η ράβδος να περιστραφεί γύρω από τον πραγματικό αυτό άξονα.
Βέβαια για να συμβαίνει αυτό ο άξονας ασκεί στη διάρκεια της κίνησης δύναμη στην ράβδο, όπως υπολογίστηκε στο δεύτερο ερώτημα.
Όταν σπάσει ο άξονας, οπότε δεν μπορεί πλέον να ασκείται η παραπάνω δύναμη, η ράβδος θα στρέφεται γύρω από κάποιον άλλον άξονα, που «δεν θα χρειάζεται να της ασκεί δύναμη». Αλλά αυτός ο άξονας δεν μπορεί παρά να είναι ο άξονας που θα περνά από το κέντρο μάζας, αφού μόνο τότε το κέντρο μάζας, μπορεί να μην έχει επιτάχυνση και δεν απαιτείται να του ασκηθεί καμιά δύναμη.
Τέτοιος πραγματικός βέβαια άξονας δεν υπάρχει, αλλά τότε η ράβδος στρέφεται γύρω από νοητό κατακόρυφο άξονα που περνά από το κέντρο μάζας Κ. “ -
Καλημερα Θοδωρη.Αυτα ολα ειναι θεματα δυναμικης και ασχετα με την γεωμετρικη σχεση ταχυτητων και επιταχυνσεων οταν η κινηση ειναι δεδομενη.Μπορει να ειναι σωστα αλλα δεν εχουν καμια σχεση με την παρουσα αναρτηση.
-
Ωραια σκέψη- ασκηση και η δική σου Διονυση , φυσικα δεν ειναι ευκολη αλλα έχει ενδιαφέρον η ανάλυση που γινεται !
-
Καλό μεσημερι Κώστα.
Σε ευχαριστώ για το σχολιασμό. -
Καλησπέρα Διονύση. Εξαιρετική. Βοηθάει πολύ την κατανόηση της σύνθετης κίνησης ελεύθερου στερεού. Πως τη λύνεις; Με την εφαρμογή της θεωρίας του σχολικού βιβλίου και τη σωστή θεώρηση για περιστροφή περί τον μόνο άξονα που δίνει σταθερότητα και που η φύση επιλέγει. Τον κύριο άξονα αδράνειας, που διέρχεται απο το κέντρο μάζας. Διάβασα το σχόλιο του Κων/νου περί αχρείαστου δεδομένου “ομογενής”. Αν δεν ομογενής δεν περιστρέφεται περί το μέσον της. Δε μπορεί να είναι γεωμετρικό σχήμα. Πρέπει να έχει μάζα, να δέχεται ομοιόμορφη βαρυτική έλξη, να παραμένει επί της Γης και να στρέφεται περί τον άξονα που διέρχεται απο το C.M. Αν το πείραμα γίνει με ρακέτα του τέννις γύρω από ποιο σημείο θα στρέφεται;
Επειδή έχουμε και επιταχύνσεις όμως, πως μπορεί να γίνει; Φαντάζομαι έναν μικροκινητήρα στο κέντρο μάζας να εκπέμπει αέριο ή ιόντα και έναν αντίστοιχο σε κάποιο σημείο της ραβδου. Οι μικροκινητηρες να έχουν αμελητέα μάζα σε σχέση με τη ράβδο… Βλέπουμε ότι πειραματικά είναι ανέφικτο. Αλλά ο στόχος της άσκησης είναι η κινηματική του στερεού και νομίζω ότι είναι άριστη η σκόπευση.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 μήνα, 1 εβδομάδα
Ένα κουίζ. Βρείτε την ταχύτητα του σημείου.
 Κάποια στιγμή τα σημεία Α και Β της ράβδου έχουν τις εικονιζόμενες ταχύτητες και επιταχύνσεις. Τα διανύσματα είναι όλα κάθετα στη ράβδο. Δίδε […]
Κάποια στιγμή τα σημεία Α και Β της ράβδου έχουν τις εικονιζόμενες ταχύτητες και επιταχύνσεις. Τα διανύσματα είναι όλα κάθετα στη ράβδο. Δίδε […]-
Γιάννη, καλημέρα.
Η επιτάχυνση του Α θα είναι ίση με την του Β συν τη σχετική του Α ως προς Β. Η σχετική θα είναι 1 προς τα δεξιά και κάθετη στην ΑΒ και θα επέχει ρόλο εφαπτομενικής (επιτροχίου). Άρα η κεντρομόλος είναι μηδενική που σημαίνει ω=0. Η ταχύτητα του Α επίσης το άθροισμα της του Β συν τη σχετική ω(ΒΑ)=0. Άρα υΑ=υΒ. -
Καλημέρα Ντίνο.
Ακριβώς ότι είπες.
https://i.ibb.co/JWQxhk5R/23.png -
Καλημερα Γιαννη και Ντινο.Προσπαθω να βρω μια υλοποιηση,ενα πραγματικο σεναριο κινησης σε μια χρονικη περιοχη γυρω απο το στιγμιοτυπο που βλεπω,τετοιο ωστε στο στιγμιοτυπο που βλεπω να ειναι αΑ = 3 m/s2 , αΒ = 2 m/s2 , υΒ = 4 m/s ,υΑ=υΒ και δεν μπορω.
Με ισες επιταχυνσεις γινεται. Με τις επιταχυνσεις που εχεις δωσει,οχι. -
Καλημέρα Κωνσταντίνε.
Περίμενε λίγο να το φτιάξω. -
Η διαφορά στο δεύτερο δεκαδικό οφείλεται στην ακρίβεια σχεδιασμού και εκτέλεσης.
-
Την έκανα βιαστικά αλλά υπάρχει και πολύ απλούστερη υλοποίηση:
Μια ράβδος είναι ακίνητη και ένας παρατηρητής στο Β έχει αρχική ταχύτητα μηδέν, αρχική γωνιακή ταχύτητα μηδέν και κατάλληλη γωνιακή επιτάχυνση.(Οποιαδήποτε κινητική κατάσταση είναι υλοποιήσιμη αν τηρήσουμε ορισμένους κανόνες όπως η φορά της κεντρομόλου, οι ίσες προβολές ταχυτήτων στη ράβδο κ.λ.π.)
-
Γιαννη δεν το καταλαβαινω.Στην φωτογραφια που δειχνεις βλεπω το ιδιο στιγμιοτυπο δεν βλεπω κινηση. Αν οι επιταχυνσεις ηταν ισες εχουμε το πολυ απλο σεναριο της μεταφορικης κινησης σκετο. Αν οι επιταχυνσεις ειναι ανισες τοτε λογικα πρεπει να εχουμε και στροφικη κινηση οποτε οι τροχιες των Α ,Β γυρω απο το στιγμιοτυπο που δινεις δεν μπορει να ειναι και οι δυο ευθυγραμμες οποτε καποια επιταχυνση πρεπει να εχει συνιστωσα κατα μηκος της ραβδου. Μπορει να κανω και λαθος.
-
Κωνσταντίνε αν πατήσεις το λινκ θα δεις το αρχείο i.p.
Η εικόνα είναι το στιγμιότυπο της αρχής της προσομοίωσης.
Ένα επόμενο στιγμιότυπο:
https://i.ibb.co/9k47tCwM/45.png -
Στο αρχικό στιγμιότυπο οι ταχύτητες και η γωνιακή ταχύτητα είναι μηδέν.
Δεν είναι όμως μηδέν η γωνιακή επιτάχυνση που ο κινητήρας επιβάλλει στη ράβδο.
Ούτε η επιτάχυνση του κίτρινου υπόβαθρου στο οποίο είναι στερεωμένος ο κινητήρας είναι μηδέν.
Όταν η γωνιακή ταχύτητα αποκτήσει μία τιμή τότε η επιτάχυνση του Α παύει να είναι κάθετη στη ράβδο. -
Ισότητα ταχυτήτων κάποια στιγμή δεν σημαίνει μεταφορική κίνηση.
Πρέπει κάθε στιγμή να είναι ίσες. -
Γιαννη δεν συμφωνω. Ο μονος τροπος να γινει αυτο ειναι το στιγμιοτυπο σου να ειναι η χρονικη στιγμη εναρξης μιας στροφικης κινησης.Αν η στροφικη κινηση προυπηρχε του στιγμιοτυπου τοτε εχουμε κεντρομολους επιταχυνσεις τουλαχιστον ενος εκ των Α,Β, αρα το σχημα που δινεις αποριπτεται. Αρα μεχρι την στιγμη αυτη του στιγμιοτυπου,η ραβδος εκανε μεταφορικη κινηση προς τα αριστερα με ολες τις ταχυτητες ισες μετρου 4 και ολες τις επιταχυνσεις ισες ας πουμε μετρου 2. Αν την στιγμη αυτη ειτε με κινητηρα ειτε με κρουση ειτε με οποιο μηχανισμο θελεις προσπαθησεις να επιβαλεις στο σημειο Α καινουργια επιταχυνση,με ασυνεχεια,τοτε η επιταχυνση του Α την στιγμη αυτη,δεν οριζεται. Δεν υπαρχει κανενας λογος η επιταχυνση του Α την στιγμη αυτη να ειναι 3(οσο εγινε μετα) και οχι 2(οσο ηταν πριν). Αρα δεν οριζεται. Αν τωρα ενας πραγματικος κινητηρας μεταβαλει την επιταχυνση του Α με συνεχη τροπο οπως γινεται στον πραγματικο κοσμο και αρχισει να περιστρεφει την ραβδο,τοτε την χρονικη στιγμη του στιγμιοτυπου η επιταχυνση του Α ειναι 2 και οχι 3.Αρα ειτε το δεις καθαρα μαθηματικα (οπως το βλεπω εγω) ειτε το δεις και φυσικα οποτε αποκλειεις τις ασυνεχειες δεν βλεπω πως το στιγμιοτυπο σου με τις δεδομενες ταχυτητες και επιταχυνσεις μπορει να ειναι σωστο.
Αυτα βεβαια ειναι δυσκολα θεματα και μαλλον κουραστικο για καποιον να τα παρακολουθησει kαι ας ειμαστε στο καφενειο μας. 🙂 ) -
Τώρα δεν είναι στην αρχή:
https://i.ibb.co/p63ZFSct/11.png -
Μία άλλη απλούστερη υλοποίηση:
https://i.ibb.co/KcYhjpqq/88.png -
Θα δεις ότι δεν πρόκειται για τη στιγμή μηδέν αλλά την 2,65 s.
-
- Φόρτωσε Περισσότερα
Καλημέρα και καλή Κυριακή.
Μια ακόμη άσκηση στην στροφορμή υλικού σημείου με αλλαγή στην ακτίνα της τροχιάς. Άσκηση που είχα προαναγγείλλει εδώ.
Ελπίζω να μην έχουν φύγει τα σχολεία από το κεφάλαιο…
Καλημέρα Διονύση, πολύ ζόρικη και ακόμα πιο πολύ διδακτική.
Κατάφερες να συνδυάσεις τη στροφορμή υλικού σημείου σε αρχικά κυκλική , κατόπιν σπειροειδή και τελικά πάλι κυκλική τροχιά) με την κινηματική στερεού…..
Respect
Μήπως ο κύλινδρος να αναφερόταν ως δίσκος, αφού αν καταλαβαίνω σωστά από μία πρώτη βιαστική ανάγνωση, είναι “ξαπλωμένος” στο οριζόντιο δάπεδο ή μήπως
βρίσκεται έξω από το δάπεδο και είναι κατακόρυφος, στρεφόμενος γύρω από οριζόντιο άξονα, κάτι σαν βαρούλκο;;;
Εγώ μέχρι και την Πέμπτη θα είμαι στερεό.
Καλημέρα Θοδωρή και σε ευχαριστώ για το σχολιασμό.
Ο κύλινδρος είναι αυτός που δείχνει το σχήμα σε κάτοψη!
Με κατακόρυφο άξονα γύρω από τον οποίο στρέφεται.
Θα μου πεις με πόσο ύψος; Ωραία μπορεί να έχει ύψος 10cm, οπότε γίνεται και δίσκος!!!
Καλημέρα παιδιά. Εξαιρετικό θέμα Διονύση!
Καλημέρα παιδιά.
Εξαιρετική και πολύ πρωτότυπη!
Καλή Κυριακή. Όμορφη και πρωτότυπη άσκηση Διονύση που θίγει πολλά.
Καλημέρα Διονύση και καλή Κυριακή.
Εξαιρετική. Πρώτα από όλα για εμάς και δευτερευόντως για τους μαθητές.
Καλημέρα Διονύση. Εξαιρετική! Και επειδή μου άρεσε είπα να περιγράψω την κίνηση και να προσθέσω κάτα ακομα:https://i.ibb.co/BHHcD0d6/SCAN-okt80.png
Καλησπέρα συνάδελφοι.
Αποστόλη, Γιάννη, Παύλο, Χρήστο και Γιώργο, σας ευχαριστώ για το σχολιασμό.
Γιώργο το τρίγωνο σκόπιμα, δεν το σχεδίασα ισοσκελές…
Καλησπέρα Διονύση.Φανηκε ότι είχες λόγο που δεν το εδωσες ισοσκελές.
Παρ’ ολα αυτά , είπα να το πάρω ισοσκελές μπας και βγάλω κανένα ¨λαγό”.
Αλλα όπως φαίνεται από τα παραπάνω δεν βγαίνει κατι καλό και σε δικαίωσαν που δεν το έδωσες ισόπλευρο.
Φοβερή Διονύση. Συγχαρητήρια!
Καλημέρα Διονύση. Πολύ καλή. Το θέμα το έχεις πλέον διερευνήσει από πολλές πλευρές, με ή χωρίς τρύπα.
Καλό μεσημέρι Δημήτρη και Ανδρέα.
Σας ευχαριστώ για το σχολιασμό.