-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 1 μέρα, 18 ώρες
Ισορροπία ράβδου και ταλάντωση υποστηρίγματος
 Λεία, λεπτή ομογενής ράβδος ΑΓ μήκους L = 2 m και μάζας Μ = 4 kg ισορροπεί οριζόντια. Στο άκρο Γ της ράβδου είναι δεμένο αβαρές και μη έκτατο κατακόρυ […]
Λεία, λεπτή ομογενής ράβδος ΑΓ μήκους L = 2 m και μάζας Μ = 4 kg ισορροπεί οριζόντια. Στο άκρο Γ της ράβδου είναι δεμένο αβαρές και μη έκτατο κατακόρυ […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μέρα, 19 ώρες
Μια Κρούση και δύο Ταλαντώσεις
 Ένα σώμα Σ μάζας Μ=1kg ηρεμεί στο κάτω άκρο ενός ιδανικού κατακόρυφου ελατηρίου, το οποίο έχει επιμηκύνει κατά 0,1m, όπως στο πρώτο σχήμα. Μετακινού […]
Ένα σώμα Σ μάζας Μ=1kg ηρεμεί στο κάτω άκρο ενός ιδανικού κατακόρυφου ελατηρίου, το οποίο έχει επιμηκύνει κατά 0,1m, όπως στο πρώτο σχήμα. Μετακινού […]-
Καλημέρα Διονύση.
Ωραίο το σύνολο !
Μια έκφραση που δεν ήταν ξεκαθαρισμένη ,με πήγε μπόλικα χρόνια πίσω ακριβώς 40, δέσμες γαρ 1985 Ζήτημα 3ο !
Σε κεκλιμένο ήταν ξαπλωμένο ελατήριο που το είχε επιμηκύνει
ένα σώμα και “συσπειρώναμε το ελατήριο …” .
Η συσπείρωση δημιούργησε πρόβλημα ,από που να ληφθεί ;
Από το φυσικό μήκος όπως εσύ ξεκαθαρίζεις η από την αρχική θέση
όπως ήθελε η επιτροπή;
Θεωρώ πως :
“συσπείρωση” =”μαζεύουν” οι σπείρες εφ’όσον το μήκος του ελατηρίου μικραίνει
“συμπίεση” =“μαζεύουν” οι σπείρες από το φυσικό μήκος και μετά
Εννοείται ότι η έκφρασή σου…”συσπείρωση (από το φυσικό μήκος του)” είναι εντάξει καθ’όσον από το φυσικό μήκος και μετά ταυτίζονται οι εκφράσεις συμπίεση και συσπείρωση .
Τελικά :
το τεντωμένο ελατήριο συσπειρώνεται μέχρι το φ.μ.χωρίς να συμπιέζεται και πέραν τούτου συμπιέζεται αλλά και συσπειρώνεται.
Να είσαι καλά -
Καλημέρα Παντελή και σε ευχαριστώ για το σχολιασμό.
Θυμάμαι, σαν χθες, τις συζητήσεις τότε στο βαθμολογικό, για το αν το ελατήριο “συσπειρώνεται” ή “συμπιέζεται”!
Γι΄αυτό προτίμησα να το επεξηγήσω, ώστε να μην προκαλέσω ξανά συζητήσεις και αντιπαραθέσεις γλωσσικού περιεχομένου…
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 3 μέρες, 17 ώρες
Ας μελετήσουμε τις ταλαντώσεις δύο σωμάτων
 Δύο σώματα Α και Β με μάζες m1=1kg και m2=4kg αντίστοιχα, τα οποία θεωρούμε υλικά σημεία αμελητέων διαστάσεων, ηρεμούν σε λείο οριζόντιο επίπεδο, δεμ […]
Δύο σώματα Α και Β με μάζες m1=1kg και m2=4kg αντίστοιχα, τα οποία θεωρούμε υλικά σημεία αμελητέων διαστάσεων, ηρεμούν σε λείο οριζόντιο επίπεδο, δεμ […]-
Καλημέρα Διονύση.
Ωραίο θέμα με μια θετική παρατήρηση για
τα παιδιά που ξέρουν να αναλύουν διαγράμματα, όπου εν προκειμένω
στα διαγράμματα του iv) επαληθεύεται το d=1m του iii) ερωτήματος!
Καλή βδομάδα
(Στη 5η σειρά της απάντησης του iii) ερωτήματος αντί “ακραίαδεξιά”νομίζω πρέπει αριστερά.) -
Καλό μεσημέρι Παντελή.
Σε ευχαριστώ για το σχολιασμό και την σωστό προσδιορισμό της θέσης (δεξιά-αριστερά)! -
καλημέρα σε όλους
πολύ καλή, Διονύση
(θα έβαζα, πάντως, ένα πρώτο “διευκολυντικό” ερώτημα: με τη βοήθεια των διαγραμμάτων να διακαιολογήσετε ότι αρχικά τα ελατήρια είναι επιμηκυμένα
“όλα τα λεφτά”, πάντως είναι το σχόλιο…
α, ναι, ο υποψήφιος θεατρικός συγγραφέας σε ευχαριστεί για την ενημέρωση) -
Καλησπέρα Βαγγέλη.
Σε ευχαριστώ για το σχολιασμό και χαίρομαι που σου άρεσε. -
ΔΙονύση καλησπέρα.
Άλλη μία όμορφη άσκηση μας παρουσιάζεις. Έχεις έμπνευση και η σειρα των ασκήσεων στις ταλαντώσεις είναι η μία καλύτερη από την άλλη. -
Καλημέρα Χρήστο και σε ευχαριστώ για το θετικό σχόλιο.
Να είσαι καλά. -
Διονύση πολύ καλή.
Πάντα μου αρέσουν οι πληροφορίες που προκύπτουν από διαγράμματα.
Το καλύτερό μου είναι το χ΄ και βεβαίως το σχόλιο. (Νομίζω ότι στο σχόλιο πρέπει να γράψεις άξονας x και όχι y, επίσης σίγουρα δεν πρέπει να μένουμε στο ότι η μόνη αρχική φάση που είναι στην ύλη είναι το π/2, αφού τέτοια θέματα βοηθούν, όχι όλους αλλά πάντως κάποιους μαθητές)
Καλημέρα -
Καλημέρα Στέφανε και σε ευχαριστώ για το σχολιασμό.
-
Καλημέρα Διονύση. Πολύ καλή. Αλλά περιέχει “απαγορευμένη” αρχική φάση και αποδεικνύει την ανοησία της οδηγίας “Να μη δίνονται και να μη ζητούνται δηλαδή οι εξισώσεις κίνησης με αρχική φάση διάφορη του 0 και του π/2 σε ερωτήματα ασκήσεων και προβλημάτων.” Δηλαδή ο ορισμός της θετικής φοράς ενός άξονα και η επίδρασή της στις αρχικές συνθήκες δεν πρέπει να διδάσκεται;
Στο σχόλιο θίγεις και ένα ακόμα θέμα. Λόγω ανυπαρξίας πολλές φορές πειραμάτων, δεν γνωρίζουν πως να βαθμολογούν άξονες. -
Πολύ ωραία Διονύση! Πολύ ωραίο επίσης το ερώτημα το τελευταίο!
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 5 μέρες, 18 ώρες
Οι επιταχύνσεις με ή χωρίς ολίσθηση.
 Ένα σώμα Σ1 ηρεμεί σε λείο οριζόντιο επίπεδο δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k, με φυσικό μήκος l0. Εκτρέπουμε το σώμα προς τα δεξιά […]
Ένα σώμα Σ1 ηρεμεί σε λείο οριζόντιο επίπεδο δεμένο στο άκρο ιδανικού ελατηρίου σταθεράς k, με φυσικό μήκος l0. Εκτρέπουμε το σώμα προς τα δεξιά […]-
Καλημέρα Διονύση. Πολύ καλή, με το κερασάκι να είναι το τελευταίο ερώτημα!
-
Γεια σου Διονύση, ωραία άσκηση.
-
Θέμα Διονύση, που αναγνωρίζεται από χιλιόμετρα….με τον βαθμό δυσκολίας
αυξημένο στο ερώτημα (ii) όπου και εμφανίζεται σχετική κίνηση…Αποστόλη, το τελευταίο ερώτημα (iii) συμφωνώ πως είναι πολύ καλό,
θα μπορούσε να υπάρξει ανεξάρτητο ως Θέμα Β, με δεδομένο πως
αρχικά θα υπάρξει ολίσθηση, αλλά κατά τη γνώμη μου έχει πιο εύκολη
απάντηση από το (ii) που δεν είναι άμεσα αντιληπτό το είδος κίνησης.Για άρση παρεξηγήσεων, αν τυχόν διαβάζει κάποιος μαθητής, η λογική
τέτοιων θεμάτων με σχετική κίνηση μεταξύ των δύο σωμάτων, τα τελευταία
χρόνια, είναι εκτός εξέτασης -
Καλημέρα και καλή Κυριακή σε όλους.
Αποστόλη, Παύλο και Θοδωρή σας ευχαριστώ για το σχολιασμό.
Θοδωρή δεν νομίζω ότι το θέμα εξετάζει την σχετική κίνηση μεταξύ των δύο σωμάτων.
Κυκλοφορούν άπειρες ασκήσεις με τα δυο σώματα, το ένα πάνω στο άλλο, να εκτελούν αατ. Απλά εδώ στο ii) ερώτημα έχουμε αυξήσει το πλάτος και υπάρχει ολίσθηση. Δεν μελετώ την κίνηση τώρα των δύο σωμάτων, παρά μόνο την αρχική επιτάχυνσή τους, θεωρώντας απλό το βήμα, η μέχρι τώρα στατική τριβή, να μετατρέπεται σε τριβή ολίσθησης.
Όσον αφορά το iii) ερώτημα αρκεί η απάντηση” Αφού η τριβή είναι τριβή ολίσθησης, κάποια μηχανική ενέργεια, μετατρέπεται σε θερμική. Άρα η ενέργεια που παρμένει στο σύστημα ως “ενέργεια ταλάντωσης” είναι μικρότερη”.
Το αν βρήκα ευκαιρία!!! την παραπάνω πρόταση να την δικαιολογήσω λίγο πιο αναλυτικά είναι μια επιλογή, που δεν καθιστά την άσκηση “εκτός ύλης”… -
Καλημερα Διονυση. Συμφωνω η ασκηση ειναι εντος υλης και πολυ καλη. Ολες οι ταχυτητες παντα σχετικες ειναι. Εκτος υλης (κακως) ειναι μονο οι διαφορετικες τιμες μετρησεων μεταξυ διαφορετικων συστηματων αναφορας λογω σχετικων ταχυτητων.
Μια παρατηρηση μονο. Αφου γραφεις οτι οι τριβες εχουν σιγουρα μειωσει την μηχανικη ενεργεια του συστηματος διοτι δεν υπαρχει περιπτωση κατα την ολισθηση να μην παραχθει θερμοτητα,αρα η ενεργεια ταλαντωσης εχει μειωθει,εκει το ερωτημα το εχεις καθαρισει.
Το θεμα των εργων των τριβων που ασκουνται στο κατω σωμα και στο πανω σωμα σε τι εχει μετατραπει κλπ ειναι αρκετα δυσκολο και δεν θα το εβαζα στην συγκεκριμενη ασκηση στο τελος ουτε ως παρατηρηση. Ειναι μεν ενδιαφερον αλλα κατα την γνωμη μου ολιγον ασχετο με την ασκηση,σε παει αλλου και ισως ο οχι πολυ καλος υποψηφιος να νομισει οτι πρεπει να το γραψει.Ειμαι γενικα της σχολης οτι οσο πιο λιγα γραφουμε τοσο το καλυτερο 🙂 -
Καλημέρα, καλή Κυριακή
Συμφωνώ Διονύση, “κυκλοφορούν άπειρες ασκήσεις με τα δύο σώματα το ένα πάνω στο άλλο, να εκτελούν ΑΑΤ”
αλλά οι 8/10 λύνονται κάνοντας χρήση “καταχρηστικών παραδοχών” (*) …..Θυμίζω δικό σου σχόλιο 11/12/2013
“Η ενέργεια που μοιράζεται είναι το 1/2 mυmax^2.
Η στατική τριβή δεν έχει τα χαρακτηριστικά μιας χωροεξαρτώμενης συντηρητικής δύναμης, οπότε ας αφήσουμε στην άκρη τις “δηλωτικές” λογικές που αποκτούν …θεολογικά χαρακτηριστικά… με το υποστηρίζουμε το ένα ή το άλλο…”12 χρόνια μετά δε νομίζω πως άλλαξαν πολλά, το βλέπω στην προ υπάρχουσα του σχολείου “γνώση” που μεταφέρουν τα περισσότερα παιδιά στην τάξη…
(*) Κωνσταντίνε, το έγραψα όσο πιο κομψά μπορούσα
Αν δεν υπήρχε σχετική κίνηση μεταξύ των σωμάτων, θα είχαν ίδια ταχύτητα και επιτάχυνση. Κατά τη γνώμη μου δεν ενδιαφέρει μόνο το στιγμιαίο γεγονός έναρξης, αλλά και η συνέχεια, αφού αυτή καθορίζεται από τις “παρελθοντικές αρχικές συνθήκες”
Το πνεύμα στο προηγούμενο σχόλιο, δεν ήταν
“κακώς αναφέρεται γιατί είναι εκτός ύλης”Καλώς αναφέρεται γιατί στο ylikonet οι αναρτήσεις στοχεύουν στην κατανόηση φαινομένων, αλλά επειδή διαβάζουν και κάποιοι μαθητές, ας γνωρίζουν πως ένα τέτοιο θέμα για εξετάσεις είναι “εντός, εκτός και επί ταυτά” και ό,τι ο καθένας καταλάβει….
Εγώ θα έβαζα το (iii) ερώτημα αυτόνομα διαμορφωμένο κατάλληλα με μοναδική απαίτηση την αναφορά στη θερμική απώλεια μηχανικής ενέργειας λόγω τριβής ολίσθησης
-
Θοδωρη καλημερα. Δεν καταλαβα καθολου αυτα που λες για καταχρηστικες μεθοδους και για χωροεξαρτωμενες και για θεολογους κλπ.τι σχεση εχουν με την συγκεκριμενη ασκηση. Εδω εχεις ερωτησεις που αφορουν μια αρχικη χρονικη στιγμη και η κινηση δεν εχει καν ξεκινησει. Τι σε νοιαζει τι θα γινει στην συνεχεια? Υπαρχει τετοια ερωτηση στην ασκηση? Επισης οταν υπαρχει ολισθηση με οχι λειες επιφανειες παραγεται θερμοτητα και η μηχανικη ενεργεια ελατωνεται. Τι εντος εκτος και επι τα αυτα λες?
-
Κωνσταντίνε καλημέρα και σε ευχαριστώ για το σχολιασμό και την τοποθέτηση.
Τώρα με το Θοδωρή, μπορείτε να συμφωνείτε σε μερικά και να διαφωνείτε σε άλλα, αλλά τι να κάνουμε, δεν γίνεται να συμφωνούμε σε όλα! -
καλό μεσημέρι σε όλους
(απέχω για τους γνωστούς λόγους: ου γαρ το γήρας και οι ατελείωτες ιατρικές εξετάσεις)
μου άρεσε, Διονύση, κυρίως διότι είναι “πραγματική”,
η τριβή είναι υπαρκτή και “αδικημένη” δύναμη, διότι την συνδέουν μόνο με απώλεια ενέργειας, ενώ ο κόσμος μας δεν θα “έστεκε” χωρίς τριβές,
(θυμίζω πώς ο αείμνηστος Βέγγος, ως Θρασύβουλας, μετέφερε δίσκο με πορτοκαλάδα, και τον εαυτόν του, στον, επίσης, αείμνηστο Ηλιόπουλο, ως Αλέκο
κάποια σχετική ανάρτηση έχω κάνει και εδώ, αλλά σιγά που μπορώ να τη βρω)
άρα, Θοδωρή, εξακολουθώ να διαφωνώ με σένα και να συμφωνώ με τον Κωνσταντίνο, στο ότι η τριβή δεν μπορεί να προκαλέσει ταλάντωση
(στο τελευταίο ερώτημα του Διονύση με ποια δύναμη το πάνω σώμα εκτελεί ταλάντωση μαζί με το κάτω;)
ούτως ή άλλως ο ορισμός της ΑΑΤ, δινόταν ως ΓΑΤ,
(άλλο ορισμός και άλλο αιτίες που την προκαλούν)
είχε γραφτεί στο κεφάλαιο των Ταλαντώσεων του σχολικού βιβλίου της Β Γενικής
(…η απομάκρυνση αρμονική συνάρτηση του χρόνου…)
στο βιβλίο της Γ οι συγγραφείς θεώρησαν, και σωστά, ότι αυτό έχει γίνει ήδη
(όλα τα βιβλία γράφτηκαν την τριετία 1997-2000)
που κάποιοι ιντρούκτορες στο ΙΕΠ αφαίρεσαν εντελώς,
(αλήθεια με ποία πραγματικά προσόντα βρέθηκαν εκεί;)
χωρίς καν να ενημερώσουν και να ζητήσουν τη γνώμη του συγγραφέα
(μέγιστη αγένεια και αντισυναδελφική συμπεριφορά)
τον οποίο και συμβαίνει να γνωρίζω “προσωπικά”… -
Βαγγέλη ολα ειναι ατμός
-
Κωνσταντίνε,
“… και χάνονται, εκτός από τον έρωτα…”
δυστυχώς φτωχύναμε από σεναριογράφους, σκηνοθέτες, ηθοποιούς…
(και κάποιοι, εκτός κυκλωμάτων, μάταια προσπαθούμε
https://ekountouris.blogspot.com/2012/03/blog-post_10.html) -
Βαγγέλη δεν ανοίγει η η κουρτίνα στη σκηνή του θεατρικού
-
καλησπέρα Παντελή
διαδικτυακά είμαι κατηγορίας Αβερέλ Ντάλτον, του αγαπημένου
δοκίμασε εδώ:
https://ekountouris.blogspot.com/search/label/%CE%88%CF%81%CE%B9%CF%82%20%CE%9C%CE%AE%CE%BB%CE%BF%CE%BD -
Καλημέρα Βαγγέλη και σε ευχαριστώ για το σχολιασμό.
Ο σύνδεσμος που ζητάει άδεια πρόσβασης δεν είναι αυτός που παραπέμπει στο Ιστολόγιό σου (αυτός λειτουργεί), αλλά ο σύνδεσμος όταν πατάς συνέχεια.
Η “συνέχεια” πρέεπι να παραπέμπει σε κάποιο αρχείο που έχεις στο Google Drive και αυτό το αρχείο πρέπει να γίνει κοινόχρηστο για να μορεί κάποιος να το ανοιξει. -
καλημέρα σε όλους
ευχαριστώ Διονύση
έκανα μια αλλαγή μήπως και…
https://ekountouris.blogspot.com/2025/11/blog-post_24.html -
Τώρα είναι εντάξει Βαγγέλη.
-
Καλημέρα Διονύση. Πολύ όμορφη.
Την προχώρησα λιγο…..https://i.ibb.co/Bb2hMs5/SCAN-NOE-90.png -
Μια άλλη προσεγγιση για το τελευταιο ΘΜΚΕhttps://i.ibb.co/9kKnQ0zx/SCAN-NOE-92.png
-
Καλησπέρα Γιώργο.
Σε ευχαριστώ για το σχολιασμό αλλά και για την παραπέρα μαθηματική επεξεργασία. -
“…….Αν, όπως στο αστρονομικό σύστημα, η μονάδα μάζας ορίζεται σε σχέση με τη δύναμη έλξης της, τότε οι διαστάσεις της M είναι L3T−2.»
Επομένως η μάζα μπορεί να μετρηθεί με ρολόγια και χάρακες. Και στον σχετικιστικό χωροχρόνο, όπου μπορούμε να μετρήσουμε και το μήκος σε μονάδες χρόνου, μπορούμε να κάνουμε το ίδιο και για την μάζα.
Έχει ενδιαφέρον το γεγονός ότι σε ένα κλασικό Νευτώνειο σύμπαν χρειαζόμαστε και χρονόμετρα και χάρακες, αλλά σε ένα σχετικιστικό σύμπαν, αυτό που περιγράφει η σύγχρονη φυσική, αρκούν μόνο τα χρονόμετρα. Με αυτά μπορούμε να ορίσουμε τις αποστάσεις και εντέλει όλες τις φυσικές ποσότητες.
Με λίγα λόγια, το «όλα είναι ατμός» στην φιλοσοφία του Θανάση Βέγγου ως Θρασύβουλα στην ταινία του 1962, … πρέπει να αντικατασταθεί με το «όλα είναι χρόνος» .
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 6 μέρες, 6 ώρες
Κάποιο φρένο ίσως;
 Δείτε παρακάτω ένα δίωρο διαγώνισμα, που δόθηκε σε μαθητές-υποψήφιους και μου έστειλε συνάδελφος Μήπως συνάδελφοι έχουμε χάσει εντελώς το μέτρο;
Δείτε παρακάτω ένα δίωρο διαγώνισμα, που δόθηκε σε μαθητές-υποψήφιους και μου έστειλε συνάδελφος Μήπως συνάδελφοι έχουμε χάσει εντελώς το μέτρο;-
Καλησπέρα Διονύση.
Έχουμε ένα φαύλο κύκλο:
Οι συνάδελφοι βάζουν τέτοια θέματα διότι οι ΚΕΕ έβαλαν τέτοια.
Οι ΚΕΕ βάζουν τέτοια θέματα διότι ξέρουν ότι οι συνάδελφοι προετοίμασαν τα παιδιά σε τέτοια θέματα.
Η Φυσική και η σκέψη των παιδιών δεν προωθείται.
Διαβάζουμε στον πρόλογο του βιβλίου 200 Puzzling Problems in Physics:
In our experience, an understanding of the laws of physics is best acquired
by applying them to practical problems. Frequently, however, the problems
appearing in textbooks can be solved only through long, complex calculations,
which tend to be mechanical and boring…..Μηχανικές και βαρετές.
Εμείς τώρα τι θα κάνουμε αν μια ΚΕΕ βάλει ένα πρόβλημα που δεν είναι βαρετό;
-Δεν περίμεναν τα παιδιά τέτοιο θέμα!
-Είναι ανφαίαρ να ζητάμε αποδείξεις!
Θυμάμαι στο παρελθόν:
-Και που είδατε κινητή τροχαλία στο σχολικό βιβλίο;Τα μέλη των ΚΕΕ προτιμούν να είναι βαρετοί από το να ακούσουν τα εξ αμάξης.
-
Γιάννη ο φαύλος κύκλος είναι το μόνο σίγουρο!
Αλλά
Αλλά είμαστε στον Νοέμβρη μήνα και βάζουμε αυτό το διαγώνισμα στα παιδιά;
Τα σκοτώνουμε!!!!
Με τι ηθικό θα συνεχίσουν;
Και αυτό πέρα από το αν τα θέματα των προηγούμενων χρόνων που επέλεξε να βάλει ο συνάδελφος είναι τώρα, εντός ύλης. Αλλο το στερεό που διδάσκαμε το 2015, άλλο το στερεό σήμερα… -
καλησπέρα σε όλους
απλό, καμία σχέση με υπερπαραγωγές, βασική αιτία μίσους της Φυσικής
υπερβολικός ο χρόνος 2 ωρών, ο μέτριος μαθητής τελειώνει σε μισή ώρα
ηθικόν δίδαγμα: ζητούνται προτάσεις για δίκαιη και σωστή αξιολόγηση παντού, Δημόσια Σχολεία, Ιδιωτικά Σχολεία, Φροντιστήρια, Βιβλία κ.α. -
Γεια σου Βαγγέλη .
Σε μισή ώρα δεν το βλέπω να τα τελειώνει. -
Διονύση υποθέτω ότι στο “εντός ύλης” έχεις ερωτηματικό.
-
Καλησπέρα Διονύση και σε όλους τους συμμετέχοντες. Βλέπουμε ένα διαγώνισμα με αντιγραφή θεμάτων Πανελλαδικών. Τι ακριβώς προσφέρει; Να δουν οι υποψήφιοι τι τους περιμένει; Ας τους συστήσει να ξεφυλλίσουν τα παλιότερα θέματα και να διαβάσουν τις λύσεις τους. Αν ένας υποψήφιος λύσει παλιά θέματα είναι έτοιμος για εξετάσεις; Γιατί αυτά και όχι κάποια άλλα;
Στο διαγώνισμα τετραμήνου, μαθητής μου στο σχολείο μου έλυσε άσκηση με ΑΔΣ χρησιμοποιώντας ροπή αδράνειας, διότι έτσι του το έμαθε ο φροντιστής του. Τον ρώτησα τι είναι η ροπή αδράνειας και δεν ήξερε!
Κάποιοι κάνουν πειράματα, δε μπορούν να προσαρμοστούν, θέλουν να εντυπωσιάσουν πόσο καλοί είναι στη λύση δύσκολων θεμάτων, θέλουν να κερδίσουν στον ανταγωνισμό ή είναι άπειροι; Όποιος κι αν είναι ο λόγος στο τέλος ο μαθητής την πληρώνει. -
Γεια σου Ανδρέα.
Όταν εξαιρούν από την ύλη τη ροπή αδράνειας σου λένε εμμέσως πλην σαφώς “Όχι ασκήσεις Δυναμικής στερεού”.
Δεν σου λένε να αντικαταστήσεις τις ράβδους του ασκησιολογίου σου με αβαρείς!Επίσης όταν θέλεις να γράψεις υcm (διότι δεν θέλεις να τρομάξεις τους μαθητές σου) πρόσθεσε το “ομογενής” στον κύλινδρο ή τροχό.
-
Γεια σας παιδιά. Πέραν του ότι είναι ένα κακόγουστο διαγώνισμα, το σημαντικότερο είναι αυτό που γράφει ο Διονύσης: τα παιδιά κάνουν έναν αγώνα και εμείς αντί να είμαστε συνοδοιπόροι, τα εξοντώνουμε ψυχολογικά από νωρίς;
-
Γιάννη, πρώτα δηλώνω Χιουμορίστας και μετά Φυσικός
προφανώς αστειεύομαι,
3 ώρες, τουλάχιστον, χρειάζονται από καλόν μαθητή -
Καλημέρα συνάδελφοι και ευχαριστώ για τα σχόλια.
Να προσυπογράψω το σχόλιο του Αποστόλη:
“Πέραν του ότι είναι ένα κακόγουστο διαγώνισμα, το σημαντικότερο είναι … ότι τα παιδιά κάνουν έναν αγώνα και εμείς αντί να είμαστε συνοδοιπόροι, τα εξοντώνουμε ψυχολογικά από νωρίς”
Όσον αφορά το χρόνο, συμφωνώ με το Βαγγέλη. Τρεις ώρες και βάλε!!!!
Και αυτό με την προϋπόθεση ότι ο μαθητής δεν χρειάζεται να προβληματιστεί σε κάτι, τα ξέρει όλα απέξω και ανακατωτά και απλώς γράφει…. -
Σχόλιο προς τον Ανδρέα Ριζόπουλο, που ανέφερε ότι: “Στο διαγώνισμα τετραμήνου, μαθητής μου στο σχολείο μου έλυσε άσκηση με ΑΔΣ χρησιμοποιώντας ροπή αδράνειας, διότι έτσι του το έμαθε ο φροντιστής του. Τον ρώτησα τι είναι η ροπή αδράνειας και δεν ήξερε!”
Το πιθανότερο Ανδρέα είναι ότι χρησιμοποίησε βοήθεια από AI για να λύσει την άσκηση την ώρα του διαγωνίσματος. Συνέβη ακριβώς το ίδιο σε εμένα και ο μαθητής δεν παραδεχόταν ούτε στους φίλους του τη χρήση ΑΙ, μέχρι που του είπα ότι η ροπή αδράνειας είναι εκτός ύλης και δεν διδάσκεται οπότε… αναγκάστηκε να το παραδεχθεί.
Μαθαίνω από φιλολόγους ότι είναι πολύ συνηθισμένο να γραφουν ολόκληρες εκθέσεις με ΑΙ!
-
-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 6 μέρες, 19 ώρες
Γραφική παράσταση ορμής – χρόνου
 Σώμα Σ μάζας M = 2 kg κινείται πάνω σε τραχύ οριζόντιο επίπεδο με το οποίο εμφανίζει συντελεστή τριβής ολίσθησης μ = 0,5. Την χρονική στιγμή t₁ το […]
Σώμα Σ μάζας M = 2 kg κινείται πάνω σε τραχύ οριζόντιο επίπεδο με το οποίο εμφανίζει συντελεστή τριβής ολίσθησης μ = 0,5. Την χρονική στιγμή t₁ το […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα
Δύο σώματα και ένα σύστημα ταλαντώνονται
 Τα δύο σώματα Σ1 και Σ2 με μάζες m1=1kg και m2=3kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, δεμένα στα άκρα δύο ιδανικών οριζοντίων ελατηρίω […]
Τα δύο σώματα Σ1 και Σ2 με μάζες m1=1kg και m2=3kg αντίστοιχα, ηρεμούν σε λείο οριζόντιο επίπεδο, δεμένα στα άκρα δύο ιδανικών οριζοντίων ελατηρίω […]-
Καλημέρα Διονύση.
Πολύ όμορφη. Έχουμε συνηθίσει τα νήματα να κόβονται ή κάποια στιγμή να χαλαρώνουν.
Και η ερώτηση βιαστικού μαθητή.
Κι αν η αρχική εκτροπή ήταν d=0,5m?
Δεν θέλω να το σκέφτομαι παιδί μου…. -
Καλημέρα Γιώργο.
Σε ευχαριστώ για το σχόλιο, αλλά μην κάνεις …”ακατάλληλες” προεκτάσεις! -
Καλησπέρα Διονύση
Εξαιρετική. Όπως αναφέρει ο Γιώργος έχουμε συνηθίσει να κόβονται τα νήματα -
Καλο μεσημέρι Χρήστο, σε ευχαριστώ για το σχολιασμό.
Ναι, δεν ήθελα να κόβονται νήματα, απλά να έχω ταλάντωση ενός συστήματος και να παίζεται ένα πινγκ-πονγκ μεταξύ συστήματος και ενός σώματος…
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 2 μέρες
Οι ταχύτητες δύο κινητών στους ίδιους άξονες.
 Μετά την πρόσφατη ανάρτηση «Γραφική παράσταση σε κοινούς άξονες», ας δούμε κάτι ανάλογο, αλλά με γραφικές παραστάσεις της ταχύτητας δύο κινητών. […]
Μετά την πρόσφατη ανάρτηση «Γραφική παράσταση σε κοινούς άξονες», ας δούμε κάτι ανάλογο, αλλά με γραφικές παραστάσεις της ταχύτητας δύο κινητών. […]-
Καλημέρα Διονύση.
Όταν το θέμα έχει και παραστάσεις είναι ομορφότερο και πρέπει να …”έλκει”.
Το τελευταίο ερώτημα κάνει το μαθητή … ανοιχτομάτη!
Πάντως δεν θα πω, μα κίνηση με μεταβλητή επιτάχυνση
δεν υπάρχει στη θεωρία ,γιατί… υπάρχει στην ερώτηση 27!
Να είσαι καλά -
Καλησπέρα και από δω Παντελή.
Σε ευχαριστώ για τον σχολιασμό.
Όσον αφορά με την μεταβλητή επιτάχυνση, προφανώς δεν μελετάω καμιά τέτοια κίνηση. Απλά μέσω της κλίσης υπολογίζεται η επιτάχυνση και … προκύπτει ότι δεν είναι σταθερή! -
Καλησπέρα Διονύση.
Άσκηση για μαθητές που έχουν εμπεδώσει καλά τι εκφράζει η κλίση και τι παίρνουμε από το διάγραμμα ταχύτητας -χρόνου.
Πολύ ωραίο το τελευταίο ερώτημα να απαντηθεί δια του αποκλεισμού. -
Καλημέρα Χρήστο.
Σε ευχαριστώ για το σχόλιο.
Όσο για το τελυταίο ερώτημα, στόχευσε στην 2η πληροφορία που πρέπει να ψάχνουν ο μαθητές όταν παιρνουν ένα διάγραμμα. Αν έχουν εμπεδώσει (όπως λες) την κλίση, να μην ξεχνούν τα εμβαδά…
-
-
H/o Μίλτος Καδιλτζόγλου έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 4 μέρες
Περνάμε στην ορμή από την Α΄ Λυκείου
 Μία ομάδα μαθητών πειραματίζεται με διάφορα σώματα αμελητέων διαστάσεων πάνω στον λείο οριζόντιο πάγκο του σχολικού τους εργαστηρίου. Αρχικά, οι μαθητές […]
Μία ομάδα μαθητών πειραματίζεται με διάφορα σώματα αμελητέων διαστάσεων πάνω στον λείο οριζόντιο πάγκο του σχολικού τους εργαστηρίου. Αρχικά, οι μαθητές […]-
Πολύ όμορφη άσκηση Μίλτο. Θα πρόσθετα και αλλα δύο ερωτήματα.
Να υπολογίσετε την απόσταση που θα έχει διανύσει το σώμα μάζα 2m όταν P2 = P και να συγκρινετε τον χρόνο κίνησης των δυο σωμάτων μέχρι να αποκτήσουν ίσες ορμές p1 = p2 = p. -
καλησπέρα σε όλους
πολύ καλή Μίλτο,
αλλά επειδή υπήρξα και ΕΚΦΕτζής, μια μικρή πρακτική παρατήρηση: σταθερή οριζόντια δύναμη στο σώμα για να φτάσει από το Α στο άκρο Β, μπορεί να ασκηθεί, μόνο, με τη βοήθεια άλλου σώματος κρεμασμένου στο σώμα, μέσω τροχαλίας στο άκρο Β, άρα το ύψος του πάγκου πρέπει να είναι και να φαίνεται μεγαλύτερο από το μήκος του, ώστε το κρεμασμένο σώμα να μην έχει φτάσει στο δάπεδο -
Καλημέρα Παύλο, καλημέρα Βαγγέλη. Ευχαριστώ για το σχολιασμό και χαίρομαι που σας άρεσε!
Σίγουρα Παύλο επιδέχεται προεκτάσεις η άσκηση, ακόμη και σύνδεση με την οριζόντια βολή. Προσπάθησα απλά να αποφύγω την κινηματική.
Ευχαριστώ πάρα πολύ Βαγγέλη για την ουσιαστική σου παρατήρηση, αναφορικά με την εκτέλεση των όσων περιγράφω. Να είσαι καλά.
-
Καλημέρα Μίλτο, καλημέρα σε όλους.
Μίλτο δεν κατάλαβα το τίτλο. Γιατί περνάμε την ορμή στην Α΄τάξη; Βλέπω άσκηση Β…
Βαγγέλη, μην βλέπεις πίσω από κάθε διατίπωση, ένα πείραμα στο εργαστήριο.
Υπάρχουν και τα εικονικά πειράματα!
Αν ο Μίλτος που δίνει την άσκηση δίνει “σταθερή δύναμη”, αυτό είναι δεδομενο αναμφισβήτητο και δεν μας ενδιαφέρει το πώς και αν αυτό μπορεί να πραγματοποιηθεί εύκολα ή δύσκολα στο εργαστήριο. -
Καλημέρα Διονύση.
Όχι, δεν διδάσκουμε την ορμή στην Α Λυκείου! Συγκρίνουμε απλά ορμές με εργαλεία της Α Λυκείου. -
Καλημέρα Μίλτο καλημέρα στην παρέα.
Όταν έχομε ‘’συγκριτικά’’ ερωτήματα δίδυμων εκτελέσεων μπορούμε, για συντόμευση, από τη μια εκτέλεση να βρούμε σχέση σχετική με το ερώτημα και να την κλωνοποιήσουμε για την δεύτερη εκτέλεση…
Αφού λοιπόν λυθεί ,όπως ο Μίλτος γεφύρωσε τις Α΄ και Β΄,
ο της Β΄πλέον μπορεί και μέσω γενικευμένου 2ο νόμου:
https://i.ibb.co/2Y541XBs/image.pngΝα πειράξω το Βαγγέλη γιατί τα θέλει …
στο εργαστήρι έχομε σώματα προσεγγίζοντας το αμελητέο στις διαστάσεις των; -
Καλημέρα Παντελή. Πάντως, αν και ο πάγκος δεν θα είναι απολύτως λείος, τη σταθερή συνισταμένη δύναμη μπορούμε να την πετύχουμε!
Ευχαριστώ και για τη δική σου προσέγγιση. Σε κάθε περίπτωση βέβαια φαίνεται ότι το τετράγωνο της ορμής που αποκτά το σώμα είναι ανάλογο της μάζας του.
-
καλημέρα σε όλους
(και Χρόνια Πολλά, λόγω της ημέρας
και αν έχει κάποια αξία ήμουν εκεί τότε, και νωρίτερα στη Νομική και ακόμη νωρίτερα στο Νέο Χημείο
και ανήκω στους πολλούς που δεν εξαργύρωσαν μετά την όποια, ακόμα και μηδενική, προσφορά τους
σήμερα, όμως, δεν θα είμαι εκεί, διότι θα πάω σε Νοσοκομείο του Περιστερίου για να μου πάρουν αίμα από αρτηρία, που είναι, κάτω από τη φλέβα, για να μετρήσουν το χαμηλό οξυγόνο μου, aiii…)
Διονύση, σωστά θα το έλεγες, αν ήταν άσκηση, όπου η εκφώνηση δεν αμφισβητείται, “η εκφώνηση είναι Ευαγγέλιο” έχω γράψει ο ίδιος, αλλά εδώ ο Μίλτος γράφει για πείραμα, που μάλιστα πραγματοποίησαν μαθητές στον εργαστηριακό πάγκο του Εργαστηρίου
Παλιοσείρα Παντελή, σωστός, και δεν χρειάζεται και το αμελητέο είναι πάντα σε σχέση με κάτι, π.χ. με το μήκος του εργαστηριακού πάγκου -
Καλημέρα Μίλτο. Όμορφη! Αλλά για Β
Λυκειου
Σίγουρα είναι εικονικο πείραμα.Ομως από την στιγμή που δεν έχουμε λείο επιπεδο καλύτερα στην εκφώνηση τέτοιων ασκήσεων να αποφεύγεται ότι γίνεται πείραμα στο εργαστηριο. -
Καλημέρα Γιώργο και σε ευχαριστώ. Φυσικά και δεν προτείνω την άσκηση για την Α, αλλά για τη Β Λυκείου.
Θα συμφωνήσω τόσο με τον Βαγγέλη, όσο και μαζί σου Γιώργο, ότι δεν χρειαζόταν ο «εκμοντερνισμός» της εκφώνησης που προσπάθησα να κάνω…
-
Καλησπέρα Μίλτο. Ωραίο το πρόβλημα. Όσον αφορά το τραπέζι του εργαστηρίου, ας θυμηθούμε την αεροτράπεζα, που δόθηκε στα Πολυκλαδικά Λύκεια, όπου οι τριβές είναι σχεδόν μηδέν. Που είναι αυτές οι τράπεζες τώρα; Αλλά μάλλον δεν τις χρειαζόμαστε. Έχουμε Τράπεζα θεμάτων και διαδραστικούς πίνακες. Έρχεται και η Τ.Ν.
-
Γεια σου Ανδρέα. Ευχαριστώ για το σχόλιο.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 4 μέρες
Με πληροφορίες από ένα διάγραμμα
 Ένα σώμα Α ηρεμεί στο κάτω άκρο ενός ιδανικού κατακόρυφου ελατηρίου, το πάνω άκρο του οποίου έχει δεθεί σε ταβάνι. Εκτρέπουμε το σώμα Α κατακόρυφα και το α […]
Ένα σώμα Α ηρεμεί στο κάτω άκρο ενός ιδανικού κατακόρυφου ελατηρίου, το πάνω άκρο του οποίου έχει δεθεί σε ταβάνι. Εκτρέπουμε το σώμα Α κατακόρυφα και το α […]-
Γεια σου Διονύση. Δηλώνω εντυπωσιασμένος!! Εξαιρετική!
(στην απάντηση του iii άλλαξε το νήμα σε ελατήριο)Να υποθέσω ότι περιμένουμε και άλλες δύο;;!!
-
Γεια σου Διονύση, θα συμφωνήσω με τον Μίλτο εξαιρετική άσκηση.
-
Καλημέρα Διονύση. Πολύ καλή όπως πάντα.
Αυτού του είδους οι ασκήσεις που αντλείς πολλές πληροφορίες από ένα διάγραμμα, είναι απαραίτητες στην διδασκαλία μας και για να μάθουν τα παιδιά να το “διαβαζουν” αλλά και να κάνουν συνδυαστικές σκέψεις.
Άλλωστε οι Κινέζοι λένε “μια εικόνα χίλιες λεξεις”! -
Διονύση πολύ καλή!
Τα διαγράμματα μπορούν να περιγράψουν με άμεσο τρόπο, χωρίς πολλά λόγια.
Μου αρέσει η αναφορά στο μήκος και όχι στις επιμηκύνσεις ή απομακρύνσεις. Είναι χρήσιμο το διαφορετικό, αυτό που ξεβολεύει τον μαθητή και του μαθαίνει να σκέφτεται.
Φαίνονται τα πλάτη, οι κλίσεις παρουσιάζουν την ταχύτητα, έχει αλλάξει η θέση ισορροπίας αλλά όχι το πλάτος, επομένως παραμένει σταθερή και η ενέργεια της ταλάντωσης, …
Μπορούμε να συζητάμε για ώρα.
Πολύ καλή, πολύ χρήσιμη, χωρίς ιδιαίτερες δυσκολίες.
Μπράβο! -
Καλησπέρα Διονύση. Έστρεψες την προσοχή σου στο χρονικά μεταβαλλόμενο μήκος του ελατηρίου, πριν και μετά την πλαστική κρούση κάτι που συνήθως δεν ασχολούμαστε και μας έδωσες εξαιρετικό θέμα. Ενδιαφέρον έχει και η μεταβολή του μήκους με την απομάκρυνση x της α.α.τ.
Με αλγεβρικές τιμές: L = L0 +ΔLΘΙ +x, x ανήκει [-Α, Α]
Εδώ
ΠΡΙΝ L = 1 + x, x ανήκει [-0,3m, 0,3m]
ΜΕΤΑ L = 1,3 + x, x ανήκει [-0,3m, 0,3m] -
Καλό απόγευμα σε όλους.
Μίλτο, Παύλο, Γιώργο, Στέφανε και Ανδρέα σας ευχαριστώ για το σχολιασμό.
Χαίρομαι που σας άρεσε… -
Γεια σου Διονύση. Πολύ δυνατό θέμα για παρατηρητικούς μαθητές!
-
Πολύ ωραία άσκηση Διονύση! Θα αρέσει σε μαθητές καθώς έχει “γριφώδες” στυλ με την παρουσίαση της γραφικής παράστασης!
-
Καλημέρα και καλή βδομάδα σε όλους.
Αποστόλη και Δημήτρη σας ευχαριστώ για το σχολιασμό. -
Καλημέρα Διονύση.
Εξαιρετική. Γιατί υπάρχει και αυτή η παραμόρφωση -
Καλημέρα Διονύση.
Προσπαθώ να καλύψω τα κενά μου…επιλύοντας και είναι μπόλικα και όμορφα, όπως ετούτη!
“Η αρχή το ήμισυ του παντός” για σχετικά ομαλή πορεία ,με το τελευταίο σκαλοπάτι να απαιτεί επι πλέον δαπάνη ενέργειας.
Καλή βδομάδα -
Χρήστο και Παντελή καλό μεσημέρι και σας ευχαριστώ για το σχολιασμό.
-
-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 4 μέρες
Σύστημα δύο σωμάτων εκτελεί α.α.τ.
 Σώμα Σ₁ με μάζα m₁ είναι σε επαφή με λείο οριζόντιο επίπεδο. Το σώμα Σ₁ είναι δεμένο στο δεξί άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k το άλλο άκρο […]
Σώμα Σ₁ με μάζα m₁ είναι σε επαφή με λείο οριζόντιο επίπεδο. Το σώμα Σ₁ είναι δεμένο στο δεξί άκρο οριζόντιου ιδανικού ελατηρίου σταθεράς k το άλλο άκρο […]-
Γεια σου Παύλο. Ενδιαφέρον σενάριο, με ωραία ερωτήματα, στη λογική και της 1.46 του σχολικού.
Φαίνεται ότι προσπαθείς να αποφύγεις την προσέγγιση που θα ανοίξει πάλι συζητήσεις, αλλά κάπου αναφέρεις για την τριβή που έχει το ρόλο της δύναμης επαναφοράς για το Σ2!
-
Γεια σου Μίλτο σε ευχαριστώ για το σχόλιο. Αναφέρθηκα αποκλειστικά σε δυνάμεις και όπως πολύ εύστοχα παρατήρησες όχι σε δυναμική ενέργεια ταλάντωσης. Δεν νομίζω να είναι λάθος ο όρος δύναμη επαναφοράς για την στατική τριβή που δέχεται το σώμα Σ₂.
-
Πολύ ωραία Παύλο! Καλοφτιαγμένη και ωραία που έδωσες δεδομένα με διαγράμματα!
-
Γεια σου Δημήτρη σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει.
-
-
H/o Ανδρέας Ριζόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 6 μέρες
Επαφή με τοίχο και κατάργηση δύναμης
 Τα σώματα Α και Β του σχήματος με μάζες αντίστοιχα mΑ = m και mΒ = 2m αντίστοιχα, συνδέονται με ελατήριο σταθεράς k και τοποθετούνται σε […]
Τα σώματα Α και Β του σχήματος με μάζες αντίστοιχα mΑ = m και mΒ = 2m αντίστοιχα, συνδέονται με ελατήριο σταθεράς k και τοποθετούνται σε […]-
Καλημέρα Ανδρέα και καλό Σαββατοκύριακο. Πολύ ωραία διερεύνηση!
Να τονίσουμε ότι το σύστημα παραμένει μονωμένο από τη στιγμή που εγκατέλειψε τον τοίχο και μετά (όπως άλλωστε αναδεικνύεις και με το ερώτημά σου). Γι’ αυτό, τα δύο σώματα δεν θα μηδενίσουν ταυτόχρονα την ταχύτητά τους, με αποτέλεσμα η μέγιστη (στη συνέχεια) δυναμική ενέργεια του ελατηρίου να είναι μικρότερη από την αρχικά αποθηκευμένη. -
Καλημέρα Μίλτο. Σε ευχαριστώ για το σχόλιό σου. Το σώμα Β μάλιστα δε μηδενίζει ποτέ την ταχύτητά του σε αντίθεση με το σώμα Α.
https://i.ibb.co/nNbPrgJg/Toix1.jpg -
Καλημέρα παιδιά.
Όμορφη άσκηση. Άσκηση που επιδέχεται αρκετές παραλλαγές και πολλά ερωτήματα.
Πχ αν στην διάρκεια του σπρωξίματος η F είχε σταθερό μέτρο ποια η μεγιστη συσπείρωση και ποια χρονική στιγμή επιτυγχάνεται?
Και μια ερώτηση με αφορμή το σχόλιο του Μίλτου. Υπάρχει περίπτωση η ταχύτητα του Α κάποια στιγμή να αποκτήσει φορά προς αριστερά? -
Καλημέρα Ανδρέα, καλημέρα σε όλους.
Ένα πανέμορφο θέμα!
Γιώργο, για να κινηθεί το Α σώμα προς τα αριστερά, πρέπει να μηδενιστεί κάποια στιγμή η ταχύτητά του. Αλλά το σώμα ξεκινά από την ηρεμία και επιταχύνεται προς τα δεξιά από το ελατήριο που επιμηκύνεται. Το σώμα Α επιταχύνεται για όσο χρόνο το ελατήριο έχει κάποια επιμήκυνση, αποκτά τη μέγιστη ταχύτητά του όταν το ελατήριο αποκτήσει για πρώτη φορά ξανά το φυσικό μήκος του και στη συνέχεια αρχίζει να επιβραδύνεται εξαιτίας της συσπείρωσης του ελατηρίου. Αυτό διαρκεί μέχρι κάποια στιγμή που η ταχύτητα του Α να μηδενιστεί για πρώτη φορά.
Αλλά από ΑΔΟ προκύπτει ότι τη στιγμή αυτή το σώμα Β έχει μέγιστη ταχύτητα και άρα από ΑΔΜΕ, το ελατήριο έχει το φυσικό μήκος του για δεύτερη φορά. Οπότε έτσι φτάσαμε σε ολοκλήρωση της ταλάντωσης και στην κατάσταση που είχαμε τη στιγμή που το Α εγκαταλείπει τον τοίχο. Συνεπώς θα ακολουθήσει η επιτάχυνση το Α ξανά προς τα δεξιά και δεν θα αποκτήσει ποτέ αρνητική ταχύτητα)
(Τα παραπάνω, μια προσπάθεια δικαιολόγησης χωρίς μελέτη ταλάντωσης με ανηγμένη μάζα ή με κινούμενο παρατηρητή…) -
Καλημέρα σε όλους. Ανδρέα με low budget υλικά βγήκε ένα όμορφο θέμα!
-
Καλό Σαββατοκύριακο. Πολύ ωραία άκσηση Ανδρέα.
-
Ερώτηση: Δεν μπορεί να υπάρχει επαφή μεταξύ δύο σωμάτων , χωρίς να υπάρχει δύναμη μεταξύ τους;
-
Στα πλαίσια της ερώτησης του Γιώργου, θα ήθελα να υπενθυμίσω την παρακάτω:
-
Ναι Διονύση.
Έτσι. Αντιμετώπιση με παρατηρητή στο cm έχει γίνει σε δικό σου θέμα? και είναι αρκετά δύσκολη -
Καλησπέρα Ανδρέα.
Το Σαββατοκύριακο που ειναι πιο χαλαρα ξεκινησα να διαβαζω τις αναρτησεις της εβδομαδας αντίστροφα.Ωραία ανάρτηση με ψραια ερωτήματα. Ξεχωριζω τα ερωτηματα ii και iv
-
Γεια σου Κωνσταντίνε γράφαμε μαζί.
Σωστός -
Καλο μεσημερι σε ολους. Ως προς το ερωτημα που εθεσε ο Γιώργος Κόμης,μια αλλη διατυπωση απαντησης (οχι πολυ διαφορετικη στην ουσια της απο αυτην του Διονύση) και εντος υλης,ειναι η εξης: H διαδικασια μεταξυ της στιγμης οπου το ελατηριο αποκτα για πρωτη φορα το φυσικο του μηκος και ταυτοχρονα το σωμα Α αποκτα την μεγιστη ταχυτητα του ,(εστω υΑ προς τα δεξια),οπως λεει ο Διονυσης,και της στιγμης οπου το ελατηριο θα αποκτησει ξανα το φυσικο του μηκος,ισοδυναμει με ελαστικη κρουση και ισχυουν δυο εξισωσεις, η ΑΔΟ και η ΑΔΜΕ.Το δευτεροβαθμιο συστημα αυτων των εξισωσεων εχει δυο ζευγαρια λυσεων ως προς τις ταχυτητες. (υΑ,υΒ) και (υΑ’,υΒ’).Την στιγμη ομως που το Α εκταλειπει τον τοιχο η ταχυτητα του ειναι μηδεν και η ταχυτητα αυτη ικανοποιει και την ΑΔΟ και την ΑΔΜΕ. Αρα αυτη ειναι η υΑ’. Τριτη λυση δεν υπαρχει. Αρα η ταχυτητα του Α δεν μπορει ποτε να ειναι προς τα αριστερα.
-
o συλλογισμός του Διονύση με σχέσεις
https://i.ibb.co/chwGJgVY/suspeirosi.jpg -
Όντως πολυ καλη ασκηση Ανδρέα.
-
Καλησπέρα συνάδελφοι, σας ευχαριστώ. Γιώργο έβαλες και μια ωραία απόδειξη σε αυτό που βλέπουμε να συμβαίνει. Διονύση, Κωνσταντίνε επίσης δώσατε ωραία εξήγηση.
Μπορούμε επίσης να σκεφτούμε και ότι αν u0 η μέγιστη ταχύτητα που αποκτά το Βhttps://i.ibb.co/KcbVssYg/elathrio1.jpg
Αποστόλη low budjet άσκηση σε σχολείο high tech…
Παύλο χαίρομαι που σου άρεσε. Επίσης καλό Σ/Κ.
Η ανάρτησή σου Μίλτο δίνει και την άλλη όψη του φαινομένου, όπου το ελατήριο ξεκινά να συμπιέζεται.
Χρήστο μακάρι να ήτανε πιο χαλαρό. Έχω αφήσει για το Σ/Κ διόρθωση διαγωνισμάτων δυο τάξεων 2 *27 = 54 γραπτά Βπροσ.
Γιάννη το θέμα το έχουμε συζητήσει εκτενώς σε ανάρτηση του Διονύση
Όχι δεν είναι οριζόντια βολή -
Ανδρέα τέτοια είδους συστήματα παντα δημιουργουν ωραίους προβληματισμούς για το πως εξελίσσεται η κίνηση των σωματων. Βασικά εργαλεία η ΑΔΟ και η ΑΔΜΕ.
Πολύ διεξοδικές οι τοποθετήσεις των συναδέλφων σχετικά με το τι θα συμβεί στην κίνηση το σώματος Α .
Βρήκα χρόνο και έκανα μια μελετη του θεματος που δείχνει το εύρος τιμών των ταχυτήτων για το κάθε σώμα . Ειναι προφανες ότι καθε μας ερώτηση – σκέψη μπορούμε να κάνουμε χρήση της ΑΔΟ και της ΑΔΜΕ για να καταληξουμε σε κάποιο αποτελέσμα που είναι δυνατόν να συμβεί ή είναι αδύνατον.
-
Καλημέρα Κώστα. Σε ευχαριστώ για τη συμμετοχή. Η ανάλυσή σου εξαιρετική. Όταν το ελατήριο έχει ΔL = 0, βλέπουμε να προκύπτουν οι σχέσεις των ταχυτήτων της ελαστικής κρούσης, όπως είπε και ο Κωνσταντίνος.
Όταν το ελατήριο έχει το φυσικό του μήκος
Α΄φορά: υΑ = 0 και υΒ = υmax
Β΄φορά: υΑ = 4/3 υmax και υΒ = 1/3υmax
Γ΄φορά: υΑ = 0 και υΒ = υmax κ.λ.π.
Όταν το ελατήριο έχει τη μέγιστη επιμήκυνση
υΑ = υΒ = u = 2/3υmax -
Καλησπέρα κ. Ριζόπουλε, πολύ ωραίο θέμα!
Κάποιες χρονικές εξισώσεις:
https://i.ibb.co/CKjQvS0s/image.jpg
Και, κάποια διαγράμματα για ταχύτητες και μήκος ελατηρίου:
https://i.ibb.co/prRt2VcR/image.jpg -
Καλημέρα Ανδρέα .
Θα έλεγα πως έχετε συνεννοηθεί με το Διονύση ως προς τη δομή των ερωτήσεων στα μοντέλα σας και ομολογώ τη θετική εκτίμησή μου!
Καλή βδομάδα -
Ανδρέα θα συμφωνήσω και εγώ πως η άσκηση είναι εξαιρετική.
Μία παρατήρηση-ιδιοτροπία δική μου:ii) Να εξηγήσετε γιατί η επαφή του σώματος Α με τον τοίχο χάνεται κάποια χρονική στιγμή t1
όταν το ελατήριο αποκτήσειτο φυσικό μήκος του.θα το έγραφαii) Να εξηγήσετε γιατί η επαφή του σώματος Α με τον τοίχο χάνεται αμέσως μετά την χρονική στιγμή t1 , κατά την οποία το ελατήριο αποκτά το φυσικό μήκος του.Τη στιγμή που το ελατήριο αποκτά το φμ του, το Α έχει μηδενική ταχύτητα υ=0 και δέχεται ΣF=0, οπότε δεν αρχίζει να κινείται, κάτι που θα συμβεί την αμέσως επόμενη στιγμή όπου θα δεχτεί ΣF=Fελ και θα αποκτήσει επιτάχυνση μη μηδενική -
Kαλημερα σε ολους. Θοδωρη δεν συμφωνω. Οταν ενα αρχικα ακινητο σωμα αρχιζει να κινειται,η εναρξη της κινησης ειναι ενα γεγονος το οποιο συμβαινει μια συγκεκριμενη χρονικη στιγμη.Αναγκαστικα την στιγμη αυτη πρεπει η ταχυτητα του σωματος να ειναι μηδεν! Γιατι; Διοτι αν δεν ηταν μηδεν τοτε μπορω να βρω μια αλλη μικροτερη χρονικη στιγμη τετοια ωστε η ταχυτητα επισης να μην ειναι μηδεν.Δεν υπαρχει αμεσως επομενη χρονικη στιγμη οπως λες. Αυτες οι εκφρασεις με το ” αμεσως επομενη ” χρησιμοποιουνται οταν ενα μεγεθος δεν οριζεται καποια χρονικη στιγμη,οπως πχ οταν κοβουμε ενα νημα ενος κρεμασμενου σωματος και θελουμε την επιταχυνση,η οποια την χρονικη στιγμη κοψιματος του νηματος δεν οριζεται.
Πως οριζεται η χρονικη στιγμη εναρξης της κινησης; Εγω για να ειναι σωστα αυτα που γραφω την οριζω ως εξης:
“Ενα αρχικα ακινητο σωμα αρχιζει να κινειται την χρονικη στιγμη t,αν υ=0 την χρονικη στιγμη t και αν υπαρχει ε>0 τετοιο ωστε υ οχι μηδεν.για καθε χρονικη στιγμη μεταξυ της t και της t+ε”
Εσυ πως την οριζεις: Xωρις μαθηματικα αν μας ρωτησει ενας μαθητης ακομα και Γυμνασιου τι σημαινει οτι ενα σωμα ξεκιναει να κινειται τι νομιζεις οτι πρεπει να πουμε;
Σχετικα με το χασιμο της επαφης,αυτη επισης ειναι ενα γεγονος το οποιο συμβαινει την ιδια χρονικη στιγμη με την εναρξη της κινησης δηλαδη την χρονικη στιγμη κατά την οποία το ελατήριο αποκτά το φυσικό μήκος του και οχι αμεσως μετα οπως λες.
Εχουμε κανει ολοκληρη συζητηση εδω με Κυριακόπουλο και Μητρόπουλο και Κουντούρη,η οποια αποτελει σεμιναριο λογικης κατα την γνωμη μου. H Audrey θέλει να ξέρει την επιτάχυνση. -
Ένα σώμα αρχίζει να κινείται έχοντας υ=0 προφανώς, εφόσον όμως έχει επιτάχυνση
διάφορη από το μηδέν. Αυτό κατανοώ, αυτό διδάσκω.Τη στιγμή που το ελατήριο αποκτά το φυσικό μήκος του δεν ασκείται δύναμη στον οριζόντιο άξονα. Μηδενική επιτάχυνση και για τα δύο σώματα.
Το Β έχει μέγιστη ταχύτητα γιατί μέχρι τότε εκτελούσε επιταχυνόμενη κίνηση,
το Α ήταν και παραμένει ακίνητο σε επαφή με τον τοίχο.Αν η εξέταση του φαινομένου σταματούσε τη στιγμή αυτή (ξαφνικός θάνατος)
το σώμα δεν θα έχανε επαφή με τον τοίχο.Επειδή όμως η εξέταση συνεχίζεται, η επαφή θα χαθεί την αμέσως επόμενη στιγμή.
Ξέχασα να σε καλημερίσω Κωνσταντίνε, επειδή βιάζομαι
-
Καλημέρα παιδιά.
Η συζήτηση δεν κατέληξε τότε, δεν θα καταλήξει και τώρα.Αν δεν ορίζεται επιτάχυνση τη στιγμή μηδέν, δεν ορίζεται ούτε δύναμη. Δηλαδή δεν υπάρχει αλληλεπίδραση τη στιγμή μηδέν!!
Όταν ο ένας εννοεί με το “επαφή” την Γεωμετρική επαφή και ο άλλος την ύπαρξη δύναμης μεταξύ των σωμάτων, τα περιθώρια συνεννόησης στενεύουν.
Είναι σαν τα “κουράδια” από τη Βαβυλωνία του Δ. Βυζαντίου. -
Γεια σου Γιάννη. Εδω μλαμε για κατι μαλλον πιο απλο. Πως οριζεται η χρονικη στιγμη κατα την οποια ξεκιναει να κινειται ενα σωμα? Την στιγμη αυτη πρεπει αναγκαστικα η ταχυτητα του να ειναι μηδεν λεω εγω. Και αυτο ισχυει και στην περιπτωση οπου η επιταχυνση του ειναι μηδεν. Εδωσα ορισμο πιο πανω σε σχολιο μου.Παρε το πιο κατω σχημα.Αν υποθεσουμε οτι η κρουση συμβαινει την χρονικη στιγμη μηδεν,τοτε ποια χρονικη στιγμη ξεκινανε να κινουνται τα σωματα? Και τα δυο την ιδια χρονικη στιγμη μηδεν λεω εγω. Αν καποιος υποστηριξει οτι το Β αρχιζει να κινειται λιγο αργοτερα μπορει να μου δωσει χρονικη στιγμη με νουμερο? Επομενη χρονικη στιγμη δεν υπαρχει.
-
Ο Θοδωρης απ οτι καταλαβα, αν δεις και το σχολιο του, ταυτισε την χρονικη στιγμη απωλειας επαφης,με την χρονικη στιγμη εναρξης της κινησεως και σε αυτο συμφωνω απολυτα μαζι του. Αρα η διαφωνια δεν βρισκεται στο τι εννοουμε με το “επαφη.” Αν δεις και το προτελευταιο του σχολιο στην εκτη σελιδα των σχολιων εδω:
Όχι δεν είναι οριζόντια βολή θα δεις οτι δεν διαφωνουμε στο τι ειναι επαφη. Η διαφωνια μας ειναι στο ποτε ειναι η εναρξη της κινησεως.
Eιναι καθαρα θεμα κινηματικης. Δεν εχει σχεση με δυναμεις. Το ειχαμε συζητησει μαζι και στην Όντρευ -
Καλησπέρα Θοδωρή, Κωνσταντίνε, Γιάννη. Θοδωρή σε ευχαριστώ. Έθεσες μια λεπτομέρεια, που απάντησαν ο Κωνσταντίνος και ο Γιάννης. Τι σκέφτομαι:
Ένα σώμα έστω ότι κάνει ομαλά επιταχυνόμενη κίνηση θετικής φοράς.
υ = αt
Για t = 0, υ = 0, δεν κινείται. Η t = 0 είναι η στιγμή που ξεκινά η αιτία που θα προκαλέσει κίνηση, αλλά το σώμα δεν έχει αποκτήσει ακόμη ταχύτητα.
Για οποιαδήποτε t > 0, υ > 0, έχει ήδη αρχίσει να κινείται.
Η έναρξη της κίνησης είναι οριακή κατάσταση. Όταν δηλαδή
lim [(t —> 0) υ(t)] > 0.
Συμφωνώ δηλαδή με το Θοδωρή.
Η κίνηση ξεκινά τη στιγμή όπου η ταχύτητα αποκτά μη μηδενική τιμή (υ ≠ 0) -
Καλησπερα Ανδρεα. Αν υ=αt ,η μικροτερη χρονικη στιγμη στην οποια αναφερεσαι,κατα την οποια η ταχυτητα αποκταει μη μηδενικη τιμη,δεν υπαρχει. Η κινηση ξεκιναει την στιγμη μηδεν διοτι καθε αλλη χρονικη στιγμη,οσο κοντα στο μηδεν και να ειναι,το σωμα κινειται. Αυτη ειναι η μονη ορισμενη χρονικη στιγμη που ειναι λογικη απαντηση,αλλοιως το ερωτημα “πότε ξεκιναει η κινηση” δεν εχει νοημα.
Επισης την στιγμη που ξεκιναει το σωμα η επιταχυνση του ειναι μηδεν ,αυτο λενε τα Μαθηματικα.
Εν παση περιπτωσει αυτου του τυπου οι διαφωνιες οπως ειπε και ο Γιαννης δεν καταληγουν καπου,οσο και να συζηταμε δεν θα βγαλουμε ακρη. -
Καλησπέρα παιδιά.
Θα διαφωνήσω και με τους δύο.
Με τον Ανδρέα διότι μηδενική ταχύτητα δεν σημαίνει ότι δεν κινείται.
Ένας ταλαντωτής κινείται συνεχώς, άσχετα αν κάποιες στιγμές έχει μηδενική ταχύτητα.
Με τον Κωνσταντίνο διότι η επιτάχυνση τη στιγμή μηδέν είναι ίση με το πηλίκο της δύναμης που δέχεται προς τη μάζα του. Έτσι θα καταλήγαμε στο ότι τη στιγμή μηδέν δεν ασκείται δύναμη, κάτι αυθαίρετο. -
Καλησπερα Γιαννη. Αναφερομουνα σε ενα αρχικα για καποιο χρονικο διαστημα ακινητο σωμα το οποιο καποια στιγμη ξεκιναει να κινειται. Στον πραγματικο κοσμο και η επιταχυνση και η δυναμη την στιγμη που ξεκιναει ειναι μηδεν. Να σε ρωτησω. Πως οριζεις την κινηση?
Τι σημαινει Μαθηματικα οτι ενα σωμα κινειται? Θα πρεπει να δωσουμε τον ιδιο ορισμο για να μπορουμε να συζηταμε. -
Ωραία.
Τη στιγμή μηδέν αφήνουμε να πέσει ένα σώμα. Τη στιγμή μηδέν δέχεται το βάρος του και κινείται με επιτάχυνση g.
Το σώμα κινείται στο χρονικό διάστημα που μεσολαβεί από τη στιγμή που το αφήσαμε ως τη στιγμή που ακινητοποιείται στο πάτωμα.Ένα σώμα είναι στερεωμένο σε ελατήριο τεντωμένο και το κρατάμε.
Τη στιγμή μηδέν το αφήνουμε. Κινείται συνέχεια άσχετα αν κάποιες στιγμές μηδενίζεται η ταχύτητά του. -
Η κίνηση αναφέρεται σε χρονικά διαστήματα.
Κάτι κινείται τη στιγμή t όταν τη στιγμή t+dt έχει μετατοπισθεί. -
Η Εννοια κινηση οριζεται θεμελιωδως σε χρονικες στιγμες ή σε χρονικα Διαστηματα? Οι επομενες προτασεις ειναι αληθεις ή ψευδεις?
1.Ενας αρμονικος ταλαντωτης την χρονικη στιγμη που βρισκεται στην θεση μεγιστης απομακρυνσης ειναι ακινητος.2..Ενας αρμονικος ταλαντωτης οταν βρισκεται στην θεση μεγιστης απομακρυνσης ειναι στιγμιαια ακινητος
Εγω ως κινηση οριζω το μη μηδενικη ταχυτητα.οποτε το ακινητος και το στιγμιαια ακινητος σημαινουν το ιδιο πραγμα. Σημαινουν υ=0.Η λεξη στιγμιαια μαλλον σημαινει οτι ελαχιστα αργοτερα δεν θα ειναι πια ακινητος.Και οι δυο προτασεις ειναι αληθεις.Εσυ πως οριζεις την κινηση? Τα σχολικα βιβλια την οριζουν?
-
Το “στιγμιαία ακίνητος” είναι περίφραση. Σημαίνει ότι η ταχύτητά του μηδενίζεται τη στιγμή εκείνη. Όμως η στιγμή εκείνη μπορεί να ανήκει στο χρονικό διάστημα της κίνησής του. Π.χ. ταλάντωση.
Π.χ. έναρξη κίνησης. -
Αρα μια χρονικη στιγμη εστω t1 κινειται ενα σωμα οταν υπαρχει μια χρονικη περιοχη κατα την οποια κινειται και η οποια περιεχει την χρονικη στιγμη t1?
Διοτι εγω το οριζω αναποδα. Ενα σωμα κινειται κατα την διαρκεια ενος χρονικου διαστηματος αν κινειται καθε χρονικη στιγμη που περιεχεται στο διαστημα.
Και η κινηση οριζεται βαση της μη μηδενικης ταχυτητας και αναφερεται σε χρονικες στιγμες..Αλλα σε ποιο βιβλιο υπαρχει ο σωστος ορισμος? Σε σχολικο βιβλιο υπαρχει? -
Και μια αλλη ερωτηση. Αν ενας μαθητης σου πει οτι ο αρμονικος ταλαντωτης στην θεση μεγιστης απομακρυνσης ακινητοποιειται ή οτι στιγμιαια ακινητοποιειται ή οτι ειναι στιγμιαια ακινητος,τον διορθωνεις? Ειναι διαφορετικο να σου πει οτι η ταχυτητα του μηδενιζεται?
-
Όχι το περιέχει. Πιστεύω το t+dt. Δηλαδή μέλλον και όχι παρελθόν για τη χρονική στιγμή Έχουμε ξαναδιαφωνήσει γι αυτό.
Όχι ούτε μαθητή διορθώνω, ούτε συνάδελφο. Καταλαβαίνω τι εννοεί. -
Γεια σου Κωνσταντίνε
Συμφωνώ με τον Γιάννη και να εισφέρω κάποια στοιχεία για το θέμα.
Η έννοια του χρόνου προκύπτει από την ανάκλαση στην ανθρώπινη συνείδηση των διαδικασιών που συμβαίνουν γύρω του και που έχουν τα εξής χαρακτηριστικά: διάρκεια, ορισμένη διάταξη εμφάνισης, και εξέλιξη κατά βήματα και φάσεις.
Τα αρχαία ελληνικά μαθηματικά δεν είχαν να πουν πολλά για την κίνηση και την μεταβολή.
Η συνέχεια -
Καλημέρα Άρη.
Κάνε το αρχείο κοινόχρηστο… -
Καλημέρα Διονύση. Υποτίθεται ήταν κοινόχρηστο.
Είναι εντάξει τώρα; -
Καλημέρα Άρη. Συνεχίζει να ζητά πρόσβαση.
-
Αποστόλη, τώρα ανοίγει το αρχείο.
Οπότε το μετέτρεψα και σε pdf, που μπορείτε να δείτε από ΕΔΩ. -
Παντελή δεν είδα το σχόλιό σου, στη ροή… Έστω και καθυστερημενα σε ευχαριστώ. Δεν τίθεται θέμα σύγκρισης, ο Διονύσης είναι πρωτοπόρος και μοναδικός δάσκαλος.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 6 μέρες
Το μονωμένο σύστημα και η ΑΔΟ
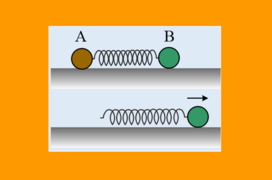 1) Στα παρακάτω σχήματα ένα σύστημα κινείται, ενώ δεν υπάρχουν τριβές, παρά μόνο μεταξύ του σώματος Σ και της σανίδας. Σε ποιες περιπτώσεις η ορμή […]
1) Στα παρακάτω σχήματα ένα σύστημα κινείται, ενώ δεν υπάρχουν τριβές, παρά μόνο μεταξύ του σώματος Σ και της σανίδας. Σε ποιες περιπτώσεις η ορμή […]-
Καλημέρα Διονύση. Πλούσιο και διδακτικό θέμα. Για κοίτα λίγο το θέμα 4…
Πώς και κύκλωσες τις σωστές απαντήσεις, χωρίς δικαιολόγηση; -
Την πάτησα Διονύση, θεωρώντας αυθαίρετα ότι το ελατήριο έχει το φυσικό του μήκος, οπότε νόμισα ότι μπέρδεψες τις μάζες…
-
Καλησπέρα Διονύση. Δεν μας έχεις συνηθίσει σε «Α Θέμα»! Μπορούν να προκύψουν ενδιαφέρουσες συζητήσεις, ευχαριστούμε!
Πάντως να γιατί το ylikonet είναι εκτός ύλης…στο 5 βάζεις συνάντηση…
-
Καλησπέρα Μίλτο και σε ευχαριστώ.
Λες να αφαιρέσω την κρούση, για να μην “συναντηθούν” τα δύο σώματα για να είμαι “εντός”;
Μήπως να βάλω δύο φορτία, όπως ο Αποστόλης και να έχουμε σκέδαση, οπότε δεν πρόκειται να έχουμε συνάντηση; 🙂 -
Καλό μεσημέρι Αποστόλη και σε ευχαριστώ για το σχολιασμό.
Οι οδηγίες επιβάλλουν στις εξετάσεις οι ερωτήσεις δικαιολόγησης, να είναι αυτές της τράπεζας.
Και επειδή δίπλα μας υπάρχουν πολύ συνάδελφοι όπου θεωρούν υποχρέωσή τους να διδάξουν όλα τα θέματα της τράπεζας και μόνο αυτά, είπα να βάλω τα ερωτήματα παραπάνω με μορφή Α θέματος. Ίσως έτσι τύχουν της προσοχής τους…
(το σχόλιο απευθύνεται σε όσους είναι φανατικοί υποστηριχτές της εξέτασης από τράπεζα θεμάτων, για ποικίλους, διατυπωμένους και μη λόγους…).
Όσον αφορά το 4ο ερώτημα.
Το σύστημα δεν είναι μονωμένο και η συνισταμένη των εξωτερικών δυνάμεων είναι η συνισταμένη των δύο βαρών, δηλαδή 3mg. Συνεπώς ο ρυθμός μεταβολής της ορμής του συστήματος είναι ίσος με 3mg.
Οπότε αν ο ρυθμός αυτός για το ένα σώμα είναι mg, για το άλλο θα είναι 2mg.
Το ίδιο προκύπτει και να βάλουμε στο παιχνίδι την δύναμη του ελατηρίου (εσωτερική δύναμη), η οποία τη στιγμή αυτή έχει μέτρο mg, με κατεύθυνση προς τα πάνω, για το σώμα Α (αντίθετη φορά για το Β). -
Γεια σου Διονύση, πολύ ωραία ερωτήματα..
-
Καλησπέρα Διονύση. Σε ευχαριστούμε για τις ερωτήσεις που η ποιότητά τους και η βοήθεια που μας δίνουν είναι ανεκτίμητη. Πολύ έξυπνες οι ασκήσεις με ελατήρια, χωρίς χρήση νόμου Hooke.
“Και επειδή δίπλα μας υπάρχουν πολύ συνάδελφοι όπου θεωρούν υποχρέωσή τους να διδάξουν όλα τα θέματα της τράπεζας και μόνο αυτά…”
Οι συνάδελφοι φροντιστές θα έχουν βρει το μπελά τους με την τράπεζα. Δεν ξέρω αν είναι εφικτό να τις προλάβουν όλες, αλλά φαντάζομαι ότι καταλαβαίνουν ότι δεν έχει νόημα αυτό το κυνήγι.
Προσωπικά δεν κάνω στο σχολείο ούτε μισή άσκηση από τράπεζα. Επιλέγω μόνο από το Υλικό και δεν έχω κανένα παράπονο, από μαθητές, ότι δεν τους λύνω από την τράπεζα. Γιατί άραγε;
Ας ελπίσουμε ότι δε θα δούμε το σενάριο “Ολα από τράπεζα”.
Αλλά το βαρέλι της απαξίωσης της Δημόσιας Παιδείας δεν έχει πάτο. -
Παύλο και Ανδρέα καλημέρα και καλό ΣΚ.
Σας ευχαριστώ για το σχολιασμό.
Ανδρέα, συμφωνώ σε όσα αναφέρεις και να τονίσω ότι “ότι δεν έχει νόημα αυτό το κυνήγι.”
Αυτό το κυνήγι να μάθουν την τάδε ή δείνα άσκηση, δεν οδηγεί πουθενά, είναι αδιεξοδη και κυρίως δεν οδηγεί στη γνώση της φυσικής… -
Καλησπέρα Διονύση.
Όπως παντα οι ερωτήσεις που θέτεις ειναι ξεχωριστές.
-
-
H/o Μίλτος Καδιλτζόγλου έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες
Εφαρμόζοντας τον 2ο νόμο σε μία φθίνουσα ταλάντωση
 Το σώμα Σ του σχήματος εκτελεί φθίνουσα ταλάντωση σε κατακόρυφη διεύθυνση, δεμένο στο ελεύθερο άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k και […]
Το σώμα Σ του σχήματος εκτελεί φθίνουσα ταλάντωση σε κατακόρυφη διεύθυνση, δεμένο στο ελεύθερο άκρο ενός κατακόρυφου ιδανικού ελατηρίου σταθεράς k και […]-
Καλημέρα Μίλτο, όμορφη άσκηση.
-
Καλημέρα Μίλτο.
Ένα θέμα εκ των ουκ άνευ, το οποίο φοβάμαι ότι η πλειοψηφία των συναδέλφων θεωρεί “εκτός ύλης”… Φανταστείτε εκτός ύλης ο 2ος νόμος του Νεύτωνα!!! ‘Η ο 2ος νόμος είναι εντός ύλης κατά παραγγελία και κατά περίπτωση…
Να υποθέσω ότι έφτασες πια στις φθίνουσες ταλαντώσεις, ενώ έχω στη σειρά για δημοσίευση, 3 ακόμη ασκήσεις πάνω στην αατ; -
Καλημέρα Παύλο, καλημέρα Διονύση και σας ευχαριστώ για το σχολιασμό!
Διονύση αναμένουμε τις ασκήσεις σου! Δεν έχω περάσει ακόμη φθίνουσες, αλλά δεν είχα κάτι να προσθέσω στο δίκτυο στην ΑΑΤ γι’ αυτό και το άλμα!Η άσκηση φυσικά Διονύση είναι στο δρόμο και τη λογική που μας δίδαξες εσύ, τόσο για τις φθίνουσες, όσο και για τις εξαναγκασμένες. Δυστυχώς, για πολλούς ο μπούσουλας είναι τα βοηθήματα του εμπορίου και το ylikonet θεωρείται εκτός ύλης…
-
Μιλτο καλησπέρα
Στις φθίνουσες κάνω τουλάχιστον ένα τέτοιο θέμα κάθε χρόνο. Η ερώτηση που κάνουν οι μαθητές ειναιναυτη που λες. Είναι αυτα εντός ύλης; Γιατί δεν έχουμε κάνει. Αλλα φυσικα οταν λες δεύτερο νομο Νεύτωνα εχεις κάνει δεν ξέρουν τι να πουν. Ακριβώς το ίδιο αν η ολίσθηση είναι εντός. -
Γεια σου Χρήστο.
Ναι, εάν μια χρονιά μπει κάτι τέτοιο (αντίστοιχα στις εξαναγκασμένες) ή σύνθετη κίνηση που δεν είναι Κ.Χ.Ο., τότε τα βοηθήματα θα γεμίσουν με επιπλέον 1000 ασκήσεις… -
Γειά σου Μίλτο. Γεια-χαρα σε όλους. Πριν 2,5 περίπου χρόνια (8-1-2023) δημοσίευσα σχετικό θέμα που όπως και η δική σου άσκηση είναι κατά τη γνώμη χρήσιμα για την κατανόηση ορισμένων πλευρών των φθινουσων ταλαντώσεων και όχι μόνο. Εκτός των άλλων έχουν τον 2ο Νόμο του Νεύτωνα στο προσκήνιο. Είναι ενδιαφέροντα και τα σχόλια που διατυπώθηκαν εκεί. Τίποτα από όσα αναφέρονται εδώ και εκεί δεν είναι εκτός ύλης. Με μια επιφύλαξη: Το Β ερώτημα της δημοσίευσης μου.
-
Καλησπέρα Γιώργο.
Εάν σου είναι εύκολο, βάλε μία παραπομπή στην άσκησή σου εδώ. -
Γεια σας παιδιά. Η άσκηση του Γιώργου εδώ.
-
Ευχαριστώ Αποστόλη. Με πρόλαβες.
-
-
H/o Παύλος Αλεξόπουλος έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 1 μέρα
Ταλάντωση – πλαστική κρούση – ταλάντωση
 Δυο ιδανικά ελατήρια σταθεράς k με φυσικό μήκος ℓ₀ βρίσκονται στην ίδια κατακόρυφο. Το ελατήριο (1) έχει το πάνω άκρο του Α στερεωμένο σε ακλόνητο σημείο […]
Δυο ιδανικά ελατήρια σταθεράς k με φυσικό μήκος ℓ₀ βρίσκονται στην ίδια κατακόρυφο. Το ελατήριο (1) έχει το πάνω άκρο του Α στερεωμένο σε ακλόνητο σημείο […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 1 μέρα
Γραφική παράσταση σε κοινούς άξονες
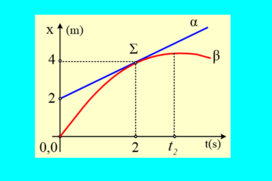 Κατά μήκος ενός ευθύγραμμου δρόμου κινούνται δύο κινητά α και β. Παίρνοντας ένα προσανατολισμένο άξονα x και κάποια στιγμή ως αρχή μέτρησης των χ […]
Κατά μήκος ενός ευθύγραμμου δρόμου κινούνται δύο κινητά α και β. Παίρνοντας ένα προσανατολισμένο άξονα x και κάποια στιγμή ως αρχή μέτρησης των χ […]-
Καλημέρα. Πολύ ωραία άσκηση Διονύση.
-
Καλημέρα παιδιά.
Πολύ καλή! -
Καλό απόγευμα Παύλο και Γιάννη.
Σας ευχαριστώ πολύ για τον σχολιασμό. -
Η ιδέα της εφαπτόμενης στην παραβολή, άρα κοινή κλίση και ίδια σταθερή και στιγμιαία ταχύτητα, πολύ καλή….
Γενικότερα όμως, υπάρχει σημαντική δυσκολία στη σχεδίαση και κατανόηση των γραφικών παραστάσεων θέσης που αντιστοιχούν σε παραβολή
-
Καλημέρα Θοδωρή και σε ευχαριστώ για το σχολιασμό και την τοποθέτηση για το πρόβλημα της αδυναμίας των μαθητών για σχεδίαση και εκμετάλλευση ενός διαγράμματος παραβολής.
Αν πρόσεξες τη λύση, μόνο τη λέξη παραβολή χρησιμοποίησα, απλά μήπως και τους μένει, ενώ η όλη αποδεικτική πορεία ξεκινά από το μηδέν.
Δεν έγραψα τίποτα για αρνητική επιτάχυνση, δεν συνέδεσα το μέγιστο με μηδενική ταχύτητα ως κάτι το γνωστό.
Κάποια πράγματα που πριν 10-15 χρόνια τα έπαιρνα σαν “γνωστά” από την θεωρία, στην παρούσα ανάρτηση τα πήρα σαν ζητούμενα… με μόνο δεδομένο το τι εκφράζει η κλίση.
-
-
Ο/η Διονύσης Μάργαρης και ο/η
Καλλιόπη Βουρουτζή είναι πλέον φίλοι πριν από 2 εβδομάδες, 2 μέρες
-
Ο/η Διονύσης Μάργαρης και ο/η
Δημήτρης Οικονόμου είναι πλέον φίλοι πριν από 2 εβδομάδες, 2 μέρες
-
Ο/η Διονύσης Μάργαρης και ο/η
Βασιλική Διακουμή είναι πλέον φίλοι πριν από 2 εβδομάδες, 2 μέρες
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες, 2 μέρες
Επιτάχυνση και δυναμική ενέργεια
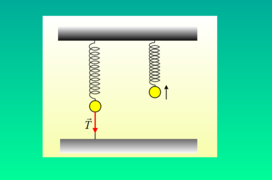 Ένα σώμα ισορροπεί, όπως στο σχήμα, στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, ενώ ταυτόχρονα συνδέεται με το έδαφος με νήμα η τάση του οποίου είναι ίση […]
Ένα σώμα ισορροπεί, όπως στο σχήμα, στο κάτω άκρο κατακόρυφου ιδανικού ελατηρίου, ενώ ταυτόχρονα συνδέεται με το έδαφος με νήμα η τάση του οποίου είναι ίση […]-
Καλησπέρα Διονύση. Ωραίο θέμα, που βοηθάει το ξεκαθάρισμα της Uταλ από την Uελ σε σύστημα κατακόρυφου ελατηρίου – σώματος. Η δυναμική ενέργεια για να οριστεί σε μια θέση απαιτεί σημείο αναφοράς. Ας υπενθυμίσουμε στους μαθητές ποιο είναι αυτό, γιατί τα ελατήρια εμφανίζονται ξαφνικά στη Γ΄Λυκείου…
-
Καλημέρα Ανδρέα.
Σε ευχαριστώ για το σχολιασμό. -
Καλημέρα Διονύση.
Μια “απλή” φαινομενικά άσκηση, σημαντική για ξεκαθάρισμα ενοιών που αναφέρονται στην α.α.τ. , όπως πλάτος, δυναμική ενέργεια ταλάντωσης αλλά και ελατηρίου!
Μια φορά Δάσκαλος μια ζωή Δάσκαλος!!! -
Καλό μεσημέρι Πρόδρομε.
Να είσαι καλά φίλε…
-
- Φόρτωσε Περισσότερα
Καλημέρα Παύλο. Ωραίο θέμα και έξυπνη εναλλακτική!!!
Καλημέρα. Δημήτρη σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει.
Καλημέρα Παύλο.
Έφερες τα πάνω- κάτω!!!
(Συνήθως το ταλαντούμενο σώμα είναι πάνω στη σανίδα).
Καλημέρα Παύλο.
Ευφάνταστη η ιδέα σου!
Το ‘κατσες… “κάτω απ’ τη μπάρα”!
Καλημέρα. Διονύση και Παντελή σας ευχαριστώ για το σχόλιο, χαίρομαι που σας αρέσει.
Καλημέρα Παύλο. Ενδιαφέρουσα και έξυπνη ιδέα! Ευχαριστούμε!
Παρατηρούμε επίσης ότι η τάση του νήματος μηδενίζεται όταν το υποστήριγμα βρίσκεται στο Μ.
Πρόσθεσε εάν θέλεις, το S.I. στην απάντηση στο (2).
Καλημέρα Παύλο. Έξυπνη ιδέα!
Γεια σας Μίλτο και Αποστόλη, χαίρομαι που σας άρεσε. Μίλτο πρόσθεσα το S.I..
Παύλο μπράβο, πολύ καλό!
Πάντα μου αρέσουν τα πρωτότυπα θέματα, που όμως μένουν μέσα σε πλαίσιο, ώστε να μπορούν να μπουν σε ένα διαγώνισμα για παράδειγμα.
Ωραία, φρέσκια ιδέα!
Μπράβο!
Γεια σου Στέφανε, σε ευχαριστώ για το σχόλιο και χαίρομαι που σου αρέσει.
Παύλε, καλημέρα.
Όμορφη άσκηση με τις δυσκολιες της.
Πάντως, με τη φυσική μας διαίσθηση, μπορούν να προβλεφτούν κάποιες απαντήσεις. Για παράδειγμα στο 1ο ερώτημα δεν μπορεί να επέλθει ανατροπή αν το υποστήριγμα βρίσκεται αριστερά του κέντρου μάζας (η ράβδος στηρίζεται δεξιά και αριστερά από το κμ).
Να ΄σαι καλά.
Καλημέρα Ντίνο και σε ευχαριστώ για το σχόλιο. Έχεις δίκιο ιδίως στο 1ο ερώτημα η απάντηση ταυτίζεται με την φυσική διαίσθηση. Να είσαι καλά.