-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 13 ώρες, 36 λεπτά
Θα αλλάξει η θερμοκρασία του αερίου;
 Τα Κονκόρντ ταξίδευαν με 700 m/s. Σε μια πτήση είχαν ένα δοχείο 22,4 λίτρων με ήλιο σε πίεση μιας ατμόσφαιρας και θερμοκρασία 273 Κ. Το δοχείο […]
Τα Κονκόρντ ταξίδευαν με 700 m/s. Σε μια πτήση είχαν ένα δοχείο 22,4 λίτρων με ήλιο σε πίεση μιας ατμόσφαιρας και θερμοκρασία 273 Κ. Το δοχείο […] -
H/o Παντελεήμων Παπαδάκης έγραψε ένα νέο άρθρο πριν από 1 μέρα, 18 ώρες
Υπερβαίνοντας το όριο
 Διαθέτουμε ένα βολτόμετρο με αντίσταση RV το οποίο έχει κλίμακα με υποδιαιρέσεις ανά 1 Volt, από 0 έως VV . Θέλουμε με το όργανο να μπορούμε να μετράμε τάσε […]
Διαθέτουμε ένα βολτόμετρο με αντίσταση RV το οποίο έχει κλίμακα με υποδιαιρέσεις ανά 1 Volt, από 0 έως VV . Θέλουμε με το όργανο να μπορούμε να μετράμε τάσε […]-
Καλημέρα Παντελή.
Ωραίο! -
Καλημέρα στη νησίδα και καλές Απόκριες.
Από το χωριό με χάλια internet …ακόμη, με αέρα φουλ μποφορ ,με θερμοκρασίες “κοντομάνικου”, σήμερα κάπως έπεσε 14C ,αλλά με βροχές ίσα για ξεδίψασμα ,πάλι καλά!
Ωθούμενος από τα κυκλώματα που αναρτώνται …
Λίγα τα ψωμιά μου εδώ …
Να είστε όλοι καλά!
Γειά σου Γιάννη ,ευχαριστώ (σε είδα μετά…) -
«με αέρα φουλ μποφορ, με θερμοκρασίες “κοντομάνικου”, σήμερα κάπως έπεσε 14C ,αλλά με βροχές» το μυαλό σου συντονίστηκε με τον καιρό Παντελή και λογικά έβγαλε όμορφη άσκηση που όμως «υπερβαίνει το όριο».
Να είσαι καλά. -
Καλό μεσημέρι Παντελή.
Εκτός ορίων εσύ, δεν το πιστεύω 🙂 -
Άρη και Διονύση καλησπέρα.
Το χωριό προσφέρεται για συντονισμό με τη φύση γενικά Άρη,
που πέραν του καιρού σου δίνει το δικαίωμα να ασχοληθείς μαζί της.
Καθάρισα τις αγκινάρες της σκάλισα της κόπρισα και ελπίζω ο μπαγάσας
που τα δυό τελευταία χρόνια σαλτάρει στο μπαξέ και αποκεφαλίζει το σύνολο,
φέτος να μου αφήσει δυό, για να τις γευτώ σαν τον καλλίτερο της εποχής μεζέ
της ρακής. Κλάδεψα και μερικές από τις αιωνόβιες αγαπημένες ελιές ,όπως και
τις κρεβατίνες, τις κληματαριές εννοώ, στην αυλή του παλαιόσπιτου.
Ερημιά χειμώνα όμως στο πανωχώρι και γενικά στο χωριό … στενάχωρη.
Και η παντέρμη μοναξιά που μου ‘λεγε η μάνα μου, αναζητά τα μικρά ανθρωπάκια, βαρίδια ισορροπίας!
Θα πετάξουμε το χαρταετό και φέτος, κάπου στου Φιλοπάππου αφού την παραμονή πετάω, μια και το Ρεθεμνιώτικο καρναβάλι το’χω ζήσει και πλέον με κουράζει .
Διονύση με βγάζει εκτός ορίων νηφαλιότητας το κρεμασμένο αγκομαχώντας ιντερνετ…
κάμποση ώρα τώρα πολεμούσα να ανεβάσω δυο τρεις φωτό από μια βόλτα στο Ρεθυμνάκι και …δεν μπόρεσα.
Να είστε καλά και καλές απόκριες -
Παντελή καλησπέρα.
Ενδιαφέρουσα σκέψη. Κάτι δεν καταλαβαίνω με το “νέο όργανο”. Η νέα αυτή διάταξη θα συνδέεται παράλληλα και το βολτόμετρο θα μετρά την τάση που περισσεύει; Δηλ. Vv+VRx=V; Tο βολτόμετρο μετρά την τάση στα άκρα που συνδέεται, δεν μπορώ να καταλάβω αν θα μετρα στην πραγματικότητα και δείχνει ένδειξη αν υλοποιηθεί τετοιο κύκλωμα. Έτσι όπως συνδέετα δεν ξερω αν θα δείχνει τάση. Είναι κάτι που δεν βλέπω;
Σε ευχαριστώ -
Καλημέρα Χρήστο.
Μιας και ο Παντελής αντιμετωπίζει προβλήματα σύνδεσης στο ίντερνετ, ας απαντήσω εγώ στο ερώτημά σου.
Έστω ότι έχουμε ένα βολτόμετρο το οποίο έχει εσωτερική αντίσταση 1.000Ω και μετρά τάσεις από 0-10V..
Το συνδέουμε παράλληλα σε μια συσκευή, βλέπουμε ένδειξη 4V και τόση είναι η τάση στα άκρα της.
Θέλουμε τώρα να μετρήσουμε τάσεις πάνω από τα 10V, με αυτό το βολτόμετρο. Τι κάνουμε;
Συνδέουμε σε σειρά με το βολτόμετρο μια αντίσταση π.χ. 3.000Ω. και έτσι δημιορυργούμε το “βολτόμετρο-1” με εσωτερική αντίσταση 4.000Ω.
Πάμε να μετρήσουμε, όπως και πριν, παράλληλα, μια άλλη συσκευή με το βολτόμετρο-1 και βλέπουμε ότι η ένδειξη του βολτομέτρου είναι 8V.
Ναι 8V είναι η τάση πάνω στην εσωτερική του αντίσταση, αλλά θα υπάρχει και μια τάση 3πλάσια, δηλαδή ίση με 24V πάνω στην προσθετη αντίσταση που έχουμε συνδέσει, οπότε η τάση στα άκρα της συσκευής δεν θα είναι 8V, αλλά 32V, δηλαδή 4πλάσια της ένδειξης του βολτομέτρου.
Έτσι βλεπουμε ένδειξη 8V και διαβάζουμε “τάση στα άκρα της συσκευής 32V”. -
Καλημέρα Χρήστο, καλημέρα Διονύση.
Πέτυχα σύνδεση και πριν το χάσω βιάζομαι…
Κοιτάζω μήπως κάτι ασύνταχτο υπάρχει στη λύση μου
και μη κατανοητό μπερδεύοντας όρους βολτόμετρο και νέο όργανο,
αλλά δεν βλέπω, άλλωστε στο σχήμα το νέο όργανο είναι στο οβαλ κίτρινο πλαίσιο.
Η Διονυσιακή ανάλυση ελπίζω πως είναι καταλυτική Χρήστο και σας ευχαριστώ.
(Ανάλογη διαδικασία γίνεται και με αύξηση της κλίμακας αμπερομέτρου βάζοντάς του παράλληλα μια Rx που θα ανοίγει ροή του επι πλέον ρεύματος.)
https://i.ibb.co/PGYbLZCd/image.png
Να και μια “καρναβαλική ” που χθες αρνούνταν να ανεβεί
Να είστε καλά -
Παντελή και ΔΙονύση καλημέρα.
Διονύση ευχαριστώ για την απάντηση. Αντιλαμβλάνομαι αυτό που λες, η απορία μου είναι αν θα λειτουργεί στην παραγματικότητα αν υλοποιηθεί τέτοια διάταξη. Με την πρωτη ευκαιρία θα το υλοποιήσω.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μέρα, 20 ώρες
Ένα ερώτημα Σ-Λ και η αξία του.
 Με αφορμή σχόλια κάτω από την ανάρτηση του Πάνου Μουρούζη «10 παρανοήσεις στο χώρο της Φυσικής», ας δούμε ένα ερώτημα που θα μπορούσε να δοθεί σε μαθη […]
Με αφορμή σχόλια κάτω από την ανάρτηση του Πάνου Μουρούζη «10 παρανοήσεις στο χώρο της Φυσικής», ας δούμε ένα ερώτημα που θα μπορούσε να δοθεί σε μαθη […]-
Καλημέρα σε όλους.
Θα ανοίξουμε το δοχείο, αφού προηγούμενα ακουστούν οι διάφορες απόψεις… -
Καλημέρα Διονύση.
Δεν ξέρω τι μπορεί να κρύβεται.
Πρώτη περίπτωση:
Η πηγή κινεί μηχανισμό που συμπιέζει ένα έμβολο. Το έμβολο συμπιέζει το αέριο.
Η θέρμανση οφείλεται σε έργο.Δεύτερη περίπτωση
Η πηγή τροφοδοτεί αντίσταση η οποία θερμαίνει ένα σιδερικό. Το σιδερικό είναι στον πάτο του δοχείου και μεταβιβάζει θερμότητα λόγω διαφοράς θερμοκρασίας σιδερικού-αερίου.Τρίτη περίπτωση.
Η πηγή θέτει σε λειτουργία μια λυχνία εκπομπής μικροκυμάτων. Αυτά θερμαίνουν το αέριο.Ο κατάλογος θα μπορούσε να εμπλουτισθεί και άλλο.
-
Να περιέχει το κουτί μια λάμπα υπερύθων που να θερμαίνει το αέριο;
Να περιέχει κινητήρα ο οποίος περιστρέφει το δοχείο του αερίου και το αέριο θερμαίνεται: (το παράδειγμα από το βιβλίο του Γιαννακόπουλου). -
Καλημέρα Διονυση. Πολλά μπορεί να είναι. Π.χ. ένα πηνίο Rhumkorff
Ή να έχουμε κρεμασμένο από την οροφή με ευτηκτο νήμα ένα σώμα και το ευτηκτο νήμα να είναι μέρος του κυκλώματος και πολλά άλλα. -
Γιάννη και Γιώργο, πολλά μπορεί να είναι τα ενδεχόμενα.
Το ερώτημα βέβαια, προσπαθεί να απαντήσει στο δίλημμα “κιθαρίστας ή ντράμερ”; 🙂
Που στην περίπτωσή μας είναι, έργο ή θερμότητα; -
Διονύση καταλαβαίνω διευρύνσεις του όρου “έργο”.
Καταλαβαίνω τι εννοεί ένας όταν λέει “ηλεκτρικό έργο”.
Όμως η διδασκόμενη Θερμοδυναμική δεν σταματάει εκεί.
Πιο κάτω Μιλάει για το P.dV το στοιχειώδες έργο.
Πιο κάτω υπολογίζει το έργο σε μια μηχανή Καρνό ή όποια άλλη.
Διότι με αυτά ασχολείται συνήθως.Δεν θα απαγορεύσουμε φυσικά έναν συσχετισμό του 1ου θερμοδυναμικού με ηλεκτρικό σύστημα. Ούτε με όποιο άλλο. Ούτε θα αλλάξουμε βιβλία της Θερμοδυναμικής που κάνουν γενικεύσεις ποικίλες.
Όμως όταν κάνεις μια ερώτηση σε μαθητή στα πλαίσια του μαθήματος της Θερμοδυναμικής Λυκείου αυτός αντιλαμβάνεται το στοιχειώδες έργο ως P.dV .Έτσι θα ψάξει να βρει αν μεταβάλλεται ο όγκος του αερίου και θα απαντήσει καταφατικά μόνο αν μεταβάλλεται ο όγκος. -
Στη συνέχεια Διονύση έρχεται η απόδοση. Το W/Qh.
Ποιο έργο θα βάλουμε στον υπολογισμό;
Αυτό που μας ενδιαφέρει για να κουνήσει το αυτοκίνητο ή και το έργο το ηλεκτρικό και το προσφερθέν από τον ηλιακό συλλέκτη:
https://i.ibb.co/23B1wbCz/15.pngΘα επαναδιατυπώσουμε τον ορισμό της απόδοσης;
-
Καλησπέρα.
Διονύση προσπαθώ να σώσω την απάντηση του μαθητή αλλά δεν τα καταφέρνω.
Q=ΔU + W
To θερμοδυναμικό σύστημα είναι το αέριο σκέτο ή το αέριο με μια αντίσταση που διαρρέεται από ρεύμα?
Ακούω αδιαβατικά τοιχώματα και σκέφτομαι.
Q = ΔU + W =0
Δηλ ΔU = -W (1)
Λέω λοιπόν δηλ μεταφέρθηκε ενέργεια μέσω έργου.Σωστό επομένως.
Το ξανακοιτώ. Πρέπει η θερμοκρασία να αυξάνεται. Αυτό συμβαίνει με βάση την 1 αν W<0
Δηλ πρέπει το αέριο να συμπιέστηκε.
Τρικυμία στο κρανίο.
Ή ο νόμος θέλει αλλαγές ή το σώνω ως εξής.
Το έργο των ηλεκτρικών δυνάμεων στα φορτία μεταφέρεται τελικά στο σύστημα ως ενέργεια και η θερμοκρασία αυξάνεται. -
Χαιρετώ τον τελευταίο σχολιαστή Γιώργο!
Παιδιά τι λέτε και για το 2ο μέρος του προβληματισμού;
Ερωτήσεις κλειστού τύπου σωστού – λάθους, όπως η παραπάνω;
Ουσιαστική εξέταση; -
Γεια σας παιδιά.
https://i.ibb.co/JjYdmfvP/35.png
Πάνω το πείραμα του Τζάουλ. Το νερό θερμαίνεται.
Κάτω μια μπαταρία τροφοδοτεί ένα μοτεράκι που ανακατεύει το αέριο.
Το αέριο θερμαίνεται.
Να πούμε και στις δύο περιπτώσεις ότι έργο προκάλεσε την αύξηση της εσωτερικής ενέργειας;
Να πούμε ότι έργο προκάλεσε την αύξηση της θερμοκρασίας του υγρού (ή αερίου) που ήρθε σε επαφή με τους έλικες και κατόπιν θερμότητα διαβιβάστηκε από το θερμό τμήμα στα υπόλοιπα τμήματα χαμηλότερης θερμοκρασίας; -
Διονύση είναι κακή ερώτηση.
Και για το λόγο που είπες (ανάκληση μιας φράσης) και για το αμφίσημο της περίπτωσης. -
Ένα θέμα μπορεί να είναι καλό για συζήτηση μεταξύ ομοτέχνων ή ως παρατήρηση σε βιβλίο πανεπιστημιακού επιπέδου και κακό σαν θέμα εξετάσεων.
-
Γεια σας παιδιά.
Να συμφωνήσω με τον Γιάννη.
Ως κακεντρεχής ή ως εξυπνάκιας θα την έβαζα σε εξετάσεις.
Σε μια χαλαρή συζήτηση στην τάξη ίσως αλλά μάλλον θα μπερδέψει …. -
Διονύση πότε θα ανοίξει το κουτί;
-
Γιάννη να … ξημερώσει η μέρα για να δούμε τι έχει μέσα 🙂
-
Να διευκρινίσω ότι το ερώτημα σκοπό είχε, όχι να διερευνήσουμε τι μπορεί να κρύβεται σε ένα “μαύρο κουτί”, ούτε το αν την ηλεκτρική ενέργεια που μεταφέρεται σε ένα σύστημα θα την θεωρήσουμε ως έργο ή ως θερμότητα, ούτε τι προβλέπει η κλασσική θερμοδυναμική, για το πού εντάσσεται η ηλεκτρική ενέργεια κατά τη γραφή του 1ου θερμοδυναμικού νόμου.
Το ερώτημα που προέκυψε στη διάρκεια της διπλανής συζήτησης που αναφέρεται στην κορυφή, εξετάζει δύο πράγματα.
Τι αξία έχει μια απάντηση σε ερώτημα Σ-Λ, με βάση ένα ορισμένο “πλαίσιο”, (λέξη που παρεξηγήθηκε…). Δηλαδή αν έχουμε ορίσει εξαρχής ότι την ηλεκτρική ενέργεια την θεωρούμε “έργο”, αυτό τέλειωσε. Θα θεωρείται έργο, αφού έτσι συμφωνήσαμε.
Δεν μας ενδιαφέρει τι συμβαίνει, δεν χρειάζεται καμιά σκέψη, κανένας προβληματισμός! Υποχρεωτική απάντηση.
Αλλά τότε τι αξία έχει ένα τέτοιο ερώτημα; Τι εξετάζει;
Αν γνωρίζουμε τη συμφωνία; -
Καλημέρα παιδιά.
Ευχαριστώ όλους τους συμμετέχοντες που έδωσαν περισσότερες εναλλακτικές λύσεις.
Οπότε Γιάννη, μιας και ξημέρωσε και δεν βλέπω άλλους ενδιαφερόμενους, ανεβάζω την απάντηση, για το τι βλέπουμε, ανοίγοντας το δοχείο…
Αλλά επειδή έχω διαπιστώσει ότι καποιοι αναγνώστες αποφεύγουν να ανοίξουν συνδέσμους, δύο εικόνες:
https://i.ibb.co/NgSzKhcJ/2026-02-19-073357.pngαλλά και 2ο δοχείο:
-
Αλλά μιας και έχουμε περάσει στην εποχή της Τ.Ν. ας δούμε και τι απάντηση μου έδωσε το ChatGPT στο παραπάνω ερώτημα.
Έχει αξία να δούμε την απάντησή του, με κλικ ΕΔΩ.
Και το συμπέρασμά του: -
Καλό μεσημέρι. Εκρίθη λοιπόν σκόπιμο η συζήτηση να μεταφερθεί εδώ
Γράφεις Διονύση: «Δηλαδή αν έχουμε ορίσει εξαρχής ότι την ηλεκτρική ενέργεια την θεωρούμε “έργο”, αυτό τέλειωσε. Θα θεωρείται έργο, αφού έτσι συμφωνήσαμε.
Δεν μας ενδιαφέρει τι συμβαίνει, δεν χρειάζεται καμιά σκέψη, κανένας προβληματισμός! Υποχρεωτική απάντηση. Αλλά τότε τι αξία έχει ένα τέτοιο ερώτημα; Τι εξετάζει;»
Δεν νομίζω ότι υπάρχει τέτοια συμφωνία ή ορισμός στην θερμοδυναμική. Υπάρχει γενικός ορισμός του έργου και εμείς καλούμαστε να κρίνουμε αν κάποια μεταφορά ενέργειας τον ικανοποιεί ή όχι. Αυτό απέχει πολύ από απλή ανάκληση απομνημονευθέντος.
Είχα αναφέρει σε άλλο σχόλιο και τον ακόλουθο ορισμό για το έργο στην θερμοδυναμική (Από το βιβλίο Perrot , A to Z of Thermodynamics) Μια αλληλεπίδραση μεταξύ δύο συστημάτων ονομάζεται έργο όταν ο προκύπτων μετασχηματισμός μπορεί να αναπαραχθεί ανεξάρτητα για κάθε σύστημα, έχοντας ως μοναδικό εξωτερικό αποτέλεσμα τη μετατόπιση μιας μάζας μέσα σε ένα βαρυτικό πεδίο. Δηλαδή όταν μπορεί, κατ’ αρχήν, να αντικατασταθεί από μια καθαρά μηχανική διαδικασία της οποίας το μόνο τελικό εξωτερικό αποτέλεσμα είναι η κατακόρυφη μετατόπιση μιας μάζας σε βαρυτικό πεδίο. Είδα ότι τον ορισμό αυτό υιοθετεί και ο Γιαννακόπουλος (σελ 32) ως τον ικανοποιητικώτερο και τον αποδίδει στον J. Gibbs τον θεμελιωτή της σύγχρονης στατιστικής θερμοδυναμικής.
Η ισχύς της θερμοδυναμικής οφείλεται στο ότι εφαρμόζεται γενικά για όλες τις φυσικές διαδικασίες χωρίς να εξετάζει την φύση τους και τις λεπτομέρειες τους -
“Δηλαδή αν έχουμε ορίσει εξαρχής ότι την ηλεκτρική ενέργεια την θεωρούμε “έργο”, αυτό τέλειωσε.”
Μπορεί να διαφωνείς Δημήτρη, αλλά ακόμη και η Τ.Ν δεν το έχει ξεκαθαρίσει και η απάντηση που έδωσε ήταν μια απάντηση που δίνεται στηριζόμενη στη “θεωρία” που λέει:
https://i.ibb.co/fVxmSmPN/2026-02-19-165626.png
Έτσι στο αρχείο που ανέβασα, η απάντηση που έδωσε (ΕΔΩ) μιλάει για έργο… -
Δηλαδή Διονύση πιστεύεις ότι δεν υπάρχει γενικός ορισμός έργου αλλά ορίζεται κατά περίπτωση τι είναι η κάθε μορφή μεταφοράς ενέργειας;
Έθεσα στην ΤΝ το ακόλουθο ερώτημα: «Πως καταλήγουμε στο αν κάποια μορφή μεταφοράς ενέργειας είναι έργο ή θερμότητα ; Με βάση κάποιον γενικό ορισμό ή με βάση κάποιες κατά περίπτωση συμφωνίες;» Μου απάντησε μεταξύ άλλωνΔεν είναι θέμα «κατά περίπτωση συμφωνίας». Υπάρχει σαφής γενικός ορισμός:
Το πραγματικά θεμελιώδες κριτήριο
Αν μπορούμε να γράψουμε τη μεταφορά ως: δW=X dY όπου: Χ γενικευμένη δύναμη (πίεση, ηλεκτρικό πεδίο κλπ) ,dΥ γενικευμένη μετατόπιση→ τότε μιλάμε για έργο. Αν όχι, και η αιτία είναι διαφορά θερμοκρασίας,
→ τότε μιλάμε για θερμότητα.
Πιο αυστηρή διατύπωση (θερμοδυναμική) Στην αντιστρεπτή περίπτωση δQrev=TdS Αυτό δείχνει ότι η θερμότητα σχετίζεται με μεταφορά εντροπίας. Το έργο δεν μεταφέρει εντροπία.
Συμπέρασμα: Η διάκριση δεν είναι αυθαίρετη σύμβαση. Είναι θεμελιωμένη: Μακροσκοπική οργάνωση → έργο. Μικροσκοπική αταξία λόγω ΔΤ → θερμότητα. Μεταφορά εντροπίας → θερμότητα. Μη μεταφορά εντροπίας → έργο -
Οταν κάνουμε σχολιασμό, κάποιας δημοσίευσης, καλό είναι να διαβάζουμε τι έχει αναρτηθεί.
Έχω γράψει:
” ας δούμε ένα ερώτημα που θα μπορούσε να δοθεί σε μαθητές, αν είχαν διδαχτεί στο μάθημα της Θερμοδυναμικής, ότι:
Σύμφωνα με την κλασική θερμοδυναμική στον 1ο Θερμοδυναμικό νόμο Q=ΔU+W:
-Θερμότητα ονομάζουμε τη μεταφορά ενέργειας που προκαλείται από διαφορά θερμοκρασίας.
-Έργο ονομάζουμε τη μεταφορά ενέργειας, με οποιονδήποτε άλλο τρόπο, που δεν προκαλείται από διαφορά θερμοκρασίας.
Το ερώτημα θα μπορούσε να είναι:
Σε ένα δοχείο με αδιαβατικά και αδιαφανή τοιχώματα περιέχεται ένα αέριο. Θερμαίνουμε το αέριο με τη βοήθεια μιας ηλεκτρικής πηγής, όπως στο σχήμα. Η ενέργεια μεταβιβάζεται στο αέριο με τη μορφή του έργου. Σωστό ή λάθος;”————– –
Έδωσα συγκεκριμένη περίπτωση, πού, σε ποιους, με ποιες προϋποθέσεις, καλείται ένας μαθητής να τοποθετηθεί.
Δεν έθεσσα ερώτημα σε καθηγητές, ούτε σε φοιτητές του τρίτου έτους (κάποτε εμείς…) που διδάχτηκαν θερμοδυναμική από το βιβλίο του Γιαννακόπουλου και τους κάλεσα να απαντήσουν, τι είναι σωστό ή τι λάθος.
Έδωσα υποθετικό ερώτημα σε μαθητές, λέγοντας μάλιστα τι ακριβώς έχουν διδαχτεί. Με μια υποθετική θεωρία που διδάχτηκαν, έδωσα ένα υποθετικό ερώτημα και τους κάλεσα να απαντήσουν αν αυτό που λέει το ερώτημα, είναι σωστό ή λάθος.
Όλα τα άλλα, δεν νομίζω ότι έχουν θέση εδώ… -
Σ’ ευχαριστώ για την ευγενική υπόδειξη. Είχα γράψει σε κάποιο σχόλιο «. Η γνώμη μου είναι ότι δεν πρέπει να μπερδεύουμε την βασική θεωρία με διδακτικές τεχνικές. Να συμφωνήσουμε πρώτα τι λέει η βασική θεωρία (η θερμοδυναμική) για το ζήτημα μας και μετά να συζητήσουμε τι και πως μπορούμε να περάσουμε στους μαθητές λυκείου.» Με άλλα λόγια δεν είναι καλό να κρυβόμαστε πίσω από τους μαθητές.
Τι θα μείνει από την συζήτηση που έγινε αν αφαιρέσουμε οτιδήποτε είναι εκτός ύλης της Β Λυκείου;
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 μέρες, 6 ώρες
Βρείτε την περίοδο της ταλάντωσης.
 Ένας άνθρωπος μάζας 100 kg έχει δεθεί με 4 ελατήρια στερεωμένα στα σημεία Α, Β, Γ και Δ. Τα λάστιχα έχουν αμελητέες μάζες και αμελητέο φυσικό μ […]
Ένας άνθρωπος μάζας 100 kg έχει δεθεί με 4 ελατήρια στερεωμένα στα σημεία Α, Β, Γ και Δ. Τα λάστιχα έχουν αμελητέες μάζες και αμελητέο φυσικό μ […]-
Διόρθωσα λάθος στην εκφώνηση:
Ελατήρια όχι λάστιχα. -
Γιάννη, να πω Τ=2π/10 sec ;;;
Ο φίλος-βοηθός μου χρειάστηκε 22s για να απαντήσει
Απάντησε σωστά;
-
Πολύ σωστά Θοδωρή.
-
Είμαι περίεργος να δω τη λύση του βοηθού.
-
Γιάννη, προφανώς δεν είναι δική μου η λύση. Θα στη στείλω στο μεηλ για να μην χαλάσω το “παιχνίδι”…. Πρόσεξε όμως 22s ο χρόνος λύσης. Σοκαριστικό;
-
Απίστευτα μικρός χρόνος!
-
Καλημέρα σας
Γιάννη, όμορφο θέμα!
https://i.ibb.co/x8GczrpX/page-0001.jpg -
Ωραίο Γιάννη. Μια λύση.
-
Η λύση της ΤΝ που μου έστειλε ο Θοδωρής:
https://i.ibb.co/Ndp3F7DF/1.png
https://i.ibb.co/pB6hNdws/2.png -
Τελικά φέρω ευθύνη για την ασάφεια της εκφώνησης.
Έπρεπε να πω ότι κρέμεται από μία σπηλιά όπως το πρωτότυπο πρόβλημα. -
Καλημέρα παιδιά.
Χρήστο και Σπύρο αυτές είναι οι λύσεις με μια συμπλήρωση:
Στις δύο σχέσεις να βάλουμε το βάρος.
https://i.ibb.co/sd73XGFY/45.png
Συμπλήρωση που δεν επηρεάζει.
-
-
H/o Παναγιώτης Κουτσομπόγερας έγραψε ένα νέο άρθρο πριν από 2 μέρες, 8 ώρες
Βατραχοδηλητήρια και δολοφονίες
 Μια πρόσφατη υπόθεση που έχει προκαλέσει διεθνείς αντιδράσεις σχετικά με «δηλητήριο από βατράχους» και τον ρόλο του στην περίπτωση του πολιτικού Αλεξέι Ναβά […]
Μια πρόσφατη υπόθεση που έχει προκαλέσει διεθνείς αντιδράσεις σχετικά με «δηλητήριο από βατράχους» και τον ρόλο του στην περίπτωση του πολιτικού Αλεξέι Ναβά […]-
Καλησπέρα Παναγιώτη
Φονικά όπλα με βάση τα δηλητήρια από βάτραχους όχι στον Αρκτικό αλλά στην Αμαζονία.
Βέλη με αιχμές που τρίφτηκαν στο δέρμα δηλητηριωδών βατράχων της ζούγκλας, όταν το δηλητήριο είναι πολύ ισχυρό.
Αλλιώς, το δηλητήριο συλλέγεται ψήνοντας τους βατράχους στη φωτιά.
Χρήση: στις εμπλοκές με μέλη άλλων φυλών και στο κυνήγι.
Το δηλητήριο κυκλοφορούσε στο αίμα των θυμάτων – όχι στο μυϊκό σύστημα, οπότε μετά το μαγείρεμα τα θηράματα ήταν ακίνδυνα για βρώση.
Ένα εντυπωσιακό χαρακτηριστικό των βατράχων με δηλητήριο που σχετίζεται με την Δαρβίνεια Προσαρμογή.
Ο βαθμός τοξικότητας των βατράχων συνδυάζεται με όσο πιο έντονα χρώματα στο δέρμα τους ενώ παράλληλα αυτά τα αμφίβια εξελίχθηκαν αποκλειστικά σε ημερήσιους θηρευτές.
Αυτά τα χρώματα σχετίζονται με τη διατροφή που έχεις ήδη αναφέρει Παναγιώτη. Μυρμήγκια, σαρανταποδαρούσες, ακάρεα.Αυτά τα χαρακτηριστικά τους λειτουργούν ως χρωματική προειδοποίηση για τους ανταγωνιστές τους και χάρις στην ανάρτησή σου έμαθα ότι ονομάζονται αποσηματισμός.
-
Καλημέρα Γιώργο και σ’ ευχαριστω για τον χρονο σου και την απαντηση – σκεφτομουν την δομή και το περιεχομενο των αναρτησεων σου, οταν με το ΑΙ εφτιαχνα αυτη την αναρτηση. Εντυπωσιακη η Δαρβίνεια Προσαρμογή οπως και ο αποσηματισμος που δεν γνωριζα, οποτε σ’ ευχαριστουμε (και) γι’ ‘αυτό!
-
-
H/o Ανδρέας Ριζόπουλος έγραψε ένα νέο άρθρο πριν από 2 μέρες, 9 ώρες
Ένας μικρός μαγνήτης αφήνεται πάνω από οριζόντιο δαχτυλίδι
 Ένας μικρός κυλινδρικός μαγνήτης νεοδύμιου (κράμα Nd₂Fe₁₄B), αφήνεται ελεύθερος να πέσει πάνω από ένα οριζόντιο μεταλλικό δακτύλιο, με το βόρειο πόλο […]
Ένας μικρός κυλινδρικός μαγνήτης νεοδύμιου (κράμα Nd₂Fe₁₄B), αφήνεται ελεύθερος να πέσει πάνω από ένα οριζόντιο μεταλλικό δακτύλιο, με το βόρειο πόλο […]-
Η ανάρτηση αφιερώνεται στο Χρήστο Αγριόδημα, αφού πηγή αποτέλεσε η δική του
-
Πολύ καλή Ανδρέα!
-
Καλημέρα παιδιά. Πολύ καλή ανάλυση Ανδρέα! Το 4ο ερώτημα απαιτητικό ακόμη και για τους υποψήφιους της Θετικής.
-
Καλησπέρα Γιάννη και Αποστόλη. Σας ευχαριστώ. Για τους περισσότερους μαθητές η επαγωγή είναι Βυl. Το πέρασμα μαγνήτη από δακτύλιο, η αναπήδηση δακτυλίου έχει πάει στα αζήτητα. Ευτυχώς που κάνουμε το εναλλασσόμενο και την αυτεπαγωγή.
-
Καλησπέρα Ανδρέα
Σε ευχαριστώ για την αφιέρωση.
Το κάλυψες πλήρως το θέμα. Όπως λες επαγωγή δεν είναι μόνο το Βul. -
Καλησπέρα Χρήστο. Να είσαι καλά! Προσωπικά μου αρέσουν πολύ τέτοιες ασκήσεις, παρά με ράβδους 1m που κάνουν πολλά μέτρα μέχρι να φτάσουν την οριακή ταχύτητα. Οι θεματοδότες προτιμούν βέβαια τις ράβδους, οπότε και εμείς…
-
Καλό απόγευμα Ανδρέα.
Συγχαρητήρια για το θέμα που μας παρουσίασες. Ένα πολύ όμορφο, αλλά και πολύ δυνατό θέμα!
Προσωπικά, για λόγους διδακτικούς, προτιμώ τις κινήσεις αγωγών και πλαισίων, αφού το επίπεδο δυσκολίας αυξάνεται κατακόρυφα με ασκήσεις οπως η παραπάνω.
Όμως αν κάποιος μαθητής μπορεί να την πλησιάσει, αυτό είναι απόδειξη ότι έχει κατανοήσει σε βάθος, πάρα πολλά πράγματα και δεν αναμασά βήματα που έμαθε, από πάρα πολλές ασκήσεις που είδε και έλυσε…
Η λογική του θέματος του 1993 σε πλήρη εκδοχή!
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 μέρες, 13 ώρες
Ας λύσουμε το πρόβλημα όπως ο Ανδρέας.
 Ένα θετικό φορτίο μπουκάρει όπως στο σχήμα σε χώρο που έχει τα εικονιζόμενα ομογενή πεδία. Πως θα λύσουμε το πρόβλημα; Όπως θέλουμε αλλά βρίσκω πιο […]
Ένα θετικό φορτίο μπουκάρει όπως στο σχήμα σε χώρο που έχει τα εικονιζόμενα ομογενή πεδία. Πως θα λύσουμε το πρόβλημα; Όπως θέλουμε αλλά βρίσκω πιο […]-
Αφιερωμένη στον Θοδωρή που έκανε την όμορφη ανάρτηση:
Μια “περίεργη” κίνηση σε σύνθετο πεδίο.Συνοδεύεται από την προσομοίωση που ανάρτησα και στην ανάρτηση του Θοδωρή.
-
Γιαννη καλησπερα .Το παρρόν δεν το εχω διαβασει ακομα. Ομως πολλες αναρτησεις περί της περιβοητης αρχης ανεξαρτησιας των κινησεων βλεπω και εχω μπερδευτει ολιγον. Τi ειναι αυτη η αρχη; Kατι ας πουμε σαν την αρχη διατηρησεως της ενεργειας; Oχι της μηχανικης,αυτης που τα βαζεις ολα μεσα. Ειναι απ οτι καταλαβα μια προταση που αφορα την αντιμεταθετικοτητα καποιων διαδικασιων. Βλεπω αναρτησεις επι αναρτησεων για το ποτε εφαρμοζεται σωστα,ποτε εφαρμοζεται λαθος,χωρις να εχω δει ορισμους και σαφεις μαθηματικες διατυπωσεις.Aν η αρχη αυτη,που δεν ειναι αρχη,αφορα την κινηματικη ενος σωματος,τοτε ειναι μονο μαθηματικα. Αν δεν δω τους αναγκαιους ορισμους και μια σαφη μαθηματικη διατυπωση αυτης της προτασεως,δεν μπορω να παρακολουθησω.Αν εχεις θεμελιωσει αλλου αυτα που ζηταω και μου διαφευγουν,δωσε μου τους συνδεσμους. Ουτε στου Ανδρεα τα κειμενα βρηκα κατι κατατοπιστικο. Μην με παρεξηγείς. 🙂
-
Καλό απόγευμα Γιάννη, αλλά στην προσομοίωση δεν μας έβαλες τον “καταλληλο” κινούμενο παρατηρητή και το τι βλέπει! 🙂
Τσάμπα το κατέβασα, για να δω μια κυκλοειδή τροχιά μόνο… -
Καλησπέρα Κωνσταντίνε.
Τα ιστορικά (Γαλιλαίος και πλοίο) τα έχει πει καλά ο Ανδρέας.
Είναι και μια τεχνική επίλυσης διαφόρων προβλημάτων.
Ένα σώμα κάνει δύο κινήσεις.
Το “κάνει δύο κινήσεις” έχει αποκτήσει δύο ερμηνείες που λένε δύο διαφορετικά πράγματα.
Η μία είναι καθαρά παιδί της Κινηματικής.
Η άλλη εμπλέκει τη Δυναμική, μιλάει για συντεταγμένες και απαιτεί ανεξαρτησία εξισώσεων. -
Ευχαριστώ Γιάννη.
Τώρα μάλιστα! Τέλειο!!! -
Η χρήση παρατηρητών έχει κάτι το “δημοκρατικό”.
Κάποιος που δεν ξέρει διαφορικές εξισώσεις μπορεί να βγάλει τις εξισώσεις κίνησης!
https://i.ibb.co/PZCGY86F/15.pngΆντε να κάνεις το ίδιο αλλιώς.
-
Τα παραπάνω παρουσιάζονται εύκολα σε παιδιά Λυκείου αν έχουν διδαχθεί σχετική ταχύτητα. Όποιος ενίσταται λέγων:
-Ναι αλλά η εμφάνιση του μυστηριώδους ηλεκτρικού πεδίου θέλει εξισώσεις Μάξγουελ!
ας το ξανασκεφτεί.
Φυσικά έχει άδικο. Δεν θέλει εξισώσεις Μάξγουελ αλλά κοινή λογική. -
Γενηθήτω το θέλημά σου Διονύση.
Κίνηση φορτίου. -
Εντυπωσιακή προσέγγιση Γιάννη! Η χρήση των παρατηρητών έχει κάτι το “δημοκρατικό”, αρκεί να έχεις την άνεση να τους χρησιμοποιείς, πράγμα που το κατέχεις καλά.
-
Ευχαριστώ Αποστόλη.
-
Kαλημερα Γιαννη. Το να βρεις το ηλεκτρικο πεδιο που βλεπει ο κινουμενος παρατηρητης ειναι μαλλον το πιο τεχνικο και δυσκολο σημειο της ασκησης,και κατα την γνωμη μου πρεπει να το εξηγησεις λιγο,αλλοιως μαλλον ο αναγνωστης θα αντιμετωπισει προβλημα. Δεν θελει βεβαιως εξισωσεις Maxwell αλλα θελει ενα μετασχηματισμο Lorentz.
Εγω το κανω ως εξης: Bαζω εναν παρατηρητη(με τηλεσκοπιο εννοειται!) να κινειται με ταχυτητα u καθετα και στα δυο πεδία.Ο Μετασχηματισμος Lorentz δινει Ε‘=γ(Ε+uxB) οπου το τονούμενο Ε‘ ειναι το καινουργιο συνολικό ηλεκτρικο πεδιο που βλεπει ο παρατηρητης με το τηλεσκοπιάκι.Αν θεσουμε u<<c τοτε Ε‘=Ε+uxB . Θελεις ο παρατηρητης αυτος να μην βλεπει καθολου ηλεκτρικο πεδιο i.e Ε‘=0.Aρα Ε+uxB =0 ή Bx(Ε+uxB)=0 ή BxΕ+Βx(uxB)=0 ή BxΕ+(ΒΒ)u)-(Βu)B)=0 Ομως Βu=0 διοτι τα Β,u ειναι καθετα εξ υποθεσεως. Οποτε BxΕ+(ΒΒ)u)=0 ή
u=-(BxΕ)/ΒΒ
Αυτο σημαινει οτι η ταχυτητα u στο δικο σου σχημα εχει φορά προς τα δεξια και μέτρο
u=E/B. Το βρήκαμε το παλληκάρι,αλλα οπως βλεπεις,αυτος ο υπολογισμος δεν ειναι καθολου απλος κατα την γνωμη μου. Χρειαζεσαι εναν μετασχηματισμο πεδιων για να προχωρησει η ασκηση.Δεν ξερω αν αυτο ειχες υπ’οψιν σου,αλλα αυτη ειναι η πιο straightforward μεθοδος την οποια μαθαινουν και φοιτητες στο πανεπιστημιο η οποια δινει και την φορά της ταχυτητας του παρατηρητη ή οποια πρεπει απο καπου να προκυψει. Εσυ φανταζομαι οτι κανεις κατι αλλο,το οποιο θελει καποιες εξηγησεις γιατι οπως ειπα,κατα την γνωμη μου ο αναγνωστης δεν θα καταλαβει.
Ως προς την (αρχη?)ανεξαρτησιας των κινησεων συνεχιζω να εχω καποιες διαφωνιες αλλα γραφω κατι και θα στο στειλω να το διαβασεις,(αν ποτέ τελειώσει) πριν το ανεβασω. -
Γεια σου Κωνσταντίνε.
Μια και μαγειρεύω θα αρκεστώ προς το παρόν σε σχόλιό μου:Όποιος ενίσταται λέγων:
-Ναι αλλά η εμφάνιση του μυστηριώδους ηλεκτρικού πεδίου θέλει εξισώσεις Μάξγουελ!
ας το ξανασκεφτεί.
Φυσικά έχει άδικο. Δεν θέλει εξισώσεις Μάξγουελ αλλά κοινή λογική.Όταν τελειώσω θα το δείξω χωρίς Μάξγουελ και Λόρεντζ.
Για την ακρίβεια θα το ξαναδείξω :
Εμφανίζεται ξαφνικά ένα ηλεκτρικό πεδίο.Θα το ξαναπώ πιο σύντομα.
-
Είμαι ο τελευταίος που θα πει ότι οι εξισώσεις Μάξγουελ και οι μετασχηματισμοί Λόρεντζ δεν χρειάζονται και μπορούν να αντικατασταθούν από την κοινή λογική και χρήση παρατηρητών.
Όμως υπάρχουν και απλά θέματα που μπορούμε να παρουσιάσουμε και σε μαθητές.
Το παρόν θέμα είναι ένα από αυτά. -
Δεν παρουσιαζονται τοσο ευκολα αυτα σε μαθητες Γιάννη. Αν ο μαθητης σου πει οτι ναι οκ το μαγνητικο πεδιο δεν μηδενιζεται,αλλα πως ξερουμε οτι ο κινουμενος παρατηρητης δεν βλεπει και διαφορετικο μαγνητικο πεδιο,εστω οχι μηδενικο,οποτε τοτε αν το μετασχηματισμενο πεδιο ειναι το Β’,τοτε το ηλεκτρικο πεδιο δεν θα ειναι Βυ. Τι θα απαντησεις? Αυτα τα πραγματα Γιαννη κατα την γνωμη μου δεν παρουσιαζονται ετσι απλα σε μαθητες. Και σε καθηγητες να τα παρουσιασεις ειτε με φορμαλισμο οπως το εκανα εγω,ειτε με απλη λογικη οπως λες εσυ,οι μισοι θα δυσκολευτουν αν εχουν καιρο να ασχοληθουν με τα θεματα αυτα. Αυτη ειναι η γνωμη μου.
-
Κωνσταντίνε τίποτα δεν είναι πολύ απλό.
Κάποια είναι απλούστερα από άλλα. -
Γιάννη τι μαγειρεψες; 🙂
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 μέρες, 21 ώρες
Ένας αγωγός επιταχύνεται σε μαγνητικό πεδίο.
 Ο αγωγός ΑΓ, μήκους l=1m, μάζας m=0,5kg και αντίστασης r=0,5Ω, ξεκινά από την ηρεμία για t=0 και επιταχύνεται προς τα δεξιά, με την επίδραση σταθερής οριζό […]
Ο αγωγός ΑΓ, μήκους l=1m, μάζας m=0,5kg και αντίστασης r=0,5Ω, ξεκινά από την ηρεμία για t=0 και επιταχύνεται προς τα δεξιά, με την επίδραση σταθερής οριζό […]-
Διονύση, καλημέρα (βρέχει, κάτι κάνει φέτος, Δερβένι 102mm από 1/1/26).
Άσκηση με απαίτηση βασικών εννοιών Φυσικής.
Κρίσιμα σημεία το βραχυκύκλωμα και το μη ακαριαίο στη μεταβολή της ταχύτητας (και όχι μόνο). -
Καλημέρα Ντίνο και σε ευχαριστώ για το σχόλιο.
Καλές είναι οι βροχές, έστω και αν στιγμιαία, φέρνουν και κάποια ταλαιπωρία…
Στην Αθήνα, τις τελευταίες μέρες.. .τίποτα, αλλά δυτικά (Ιόνιο μεριά…) μου λένε ότι το έχει παρακάνει!!!! -
Καλημέρα Διονύση
Πολύ καλή η διευρένιση στους ρυθμούς μεταβολής και άκρως διδακτική που απαιτεί κατανόηση φυσικής. -
Καλησπέρα Διονύση. Διδακτική η άσκησή σου που θίγει βασικές έννοιες απαραίτητες στη φαρέτρα γνώσεών του υποψηφίου.
Το βραχυκύκλωμα που λέει και ο Ντίνος είναι κομβικό σημείο για τη λύση της άσκησης.
Πολλοί μαθητές δεν το παίρνουν είδηση…
Τα ερωτήματα που θέτεις είναι εύστοχα ως συνήθως.
Μια φορά Δάσκαλος για πάντα Δάσκαλος! -
Χρήστο και Πρόδρομε, καλό απόγευμα και σας ευχαριστώ για το σχολαισμό.
Είπα να ξικινήσω την επαγωγή με κάτι από τα πολύ γνωστά και σίγουρα διδαγμένα, (ρυθμοί μεταβολής), για να δοθεί η ευκαιρία τους μαθητές, να δουν αν τα έχουν εμπεδώσει ή τα έχουν μάθει τυπικά… -
Καλησπέρα Διονύση. Τι σου κάνει ένας διακόπτης. Πριν ήταν αρκετή η δύναμη για να παρέχει στο σύστημα την ηλεκτρική ενέργεια, αλλά μετά χρειάζεται να “τραβάει” και από την κινητική ενέργεια για να δώσει την ηλεκτρική ενέργεια που χρειάζεται το κύκλωμα. Μάλιστα, πριν υπολογίσουμε το ρυθμό dK/dt φαίνεται ότι η δύναμη Laplace μετασχηματίζει περισσότερη ενέργεια από ότι παίρνει…
Όσον αφορά τη βροχή, εδώ στην Πάτρα δε λέει να σταματήσει. Στην Ακτή Δυμαίων, παραλιακός δρόμος, χρειάζεται φουσκωτό. Συσκέψεις επί συσκέψεων Περιφέρεια, Δήμος, Λιμενικό, χρόνια τώρα: “Μα γιατί γεμίζει νερά;”
Η θάλασσα είναι στα 100m. Κάποια αυλάκια με σχάρες δε θα έκαναν τη δουλειά; 🙁
-
-
H/o Μουρούζης Παναγιώτης έγραψε ένα νέο άρθρο πριν από 3 μέρες, 10 ώρες
Ποιο είναι πιο βαρύ; 1 κιλό σίδηρο ή 1 κιλό βαμβάκι;
 Επειδή αυτές τις ημέρες αναρτήθηκαν αρκετά άρθρα στον ιστότοπο που ήταν σε πολύ υψηλό επίπεδο για τους μαθητές μας, σκέφτηκα να αναρτήσω κάτι πολύ […]
Επειδή αυτές τις ημέρες αναρτήθηκαν αρκετά άρθρα στον ιστότοπο που ήταν σε πολύ υψηλό επίπεδο για τους μαθητές μας, σκέφτηκα να αναρτήσω κάτι πολύ […]-
Πάνο θυμάμαι τον Ανδρέα όταν μας πρότεινε ένα αφοπλιστικό πείραμα:
-Πιστεύουν τα παιδιά ότι το βαρύ πέφτει πιο γρήγορα. Σκίστε από ένα φύλλο Α4 ένα μικρό κομματάκι και κάντε το μπαλάκι. Ρωτήστε πιο είναι πιο βαρύ και θα καταλάβουν ότι είναι πιο βαρύ το μεγάλο κομμάτι. Αφήστε τα να πέσουν και θα δουν ταχύτερη πτώση του ελαφρότερου!Μου άρεσε πολύ η ιδέα και το έκανα κάθε χρονιά.
Μια χρονιά ρωτάω:
-Ποιο είναι πιο βαρύ;
-Το μικρό που κάνατε μπαλάκι.
-Γιατί;
-Γιατί θα πέσει πιο γρήγορα.Όταν είπα τη στιχομυθία στον Ανδρέα ενθουσιάστηκε. Είπε περίπου:
-Τελικά ταυτίζουν το “είναι βαρύ” με το “πέφτει γρήγορα”. -
Κοβουμε ενα φυλλο χαρτι, το βαζουμε πισω απο ενα βιβλιο , τα αφηνουμε ελευθερα πεφτουν ταυτόχρονα
-
Ωραίο Θανάση!
-
Πάνο μιλώντας με καθημερινή γλώσσα ονομάζουμε “βαρύ” κάτι που σηκώνουμε πιο δύσκολα.
https://i.ibb.co/prLqn5hj/DSC-0542.jpg
Έτσι ο πύθωνας είναι λιγότερο βαρύς από ένα άτομο ίδιας μάζας.
(Μουσείο ερπετών Μελιδονίου). -
Ο Ανδρέας μου λείπει. Στα συνέδρια των Φυσικών πήγαινα τα τελευταία 20 χρόνια πριν το θάνατό του, με τη χαρά της αντάμωσής μας. Μας λείπει σε όλους μας νομίζω. Σου είχε ιδιαίτερη αδυναμία. Μου το είχε εκμυστηρευτεί πολλές φορές.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 4 μέρες, 7 ώρες
Είδωλο φορτίο.
 Έχουμε μια συμπαγή μεταλλική γειωμένη σφαίρα ακτίνας R. Σε απόσταση d από την επιφάνειά της πλησιάζουμε ένα θετικό φορτίο Q. Πόση δύναμη δέ […]
Έχουμε μια συμπαγή μεταλλική γειωμένη σφαίρα ακτίνας R. Σε απόσταση d από την επιφάνειά της πλησιάζουμε ένα θετικό φορτίο Q. Πόση δύναμη δέ […]-
Καλημερα Γιαννη. Αυτοτο ερωτημα ειναι κλασικο και υπαρχει σχεδον σε ολα τα βιβλια ηλεκτρομαγνητισμου.Αν βαλουμε ενα φορτιο ειδωλο q’=-Rq/(d+R) στην καταλληλη θεση ( x=RR/(d+R) απο το κεντρο προς το q ) και εκφρασουμε το δυναμικο παντου στο επιπεδο του σχηματος σου σε πολικες συντεταγμενες,τοτε αν βαλουμε r=R το δυναμικο μηδενιζεται.Aρα ειναι μηδεν και στο Α και σε ολα τα αλλα σημεια της σφαιρας. Ετσι το θυμαμαι. Εκτος αν εχεις υποψιν σου καποιο άλλο τρυκ.
-
Καλημέρα και από εδώ Γιάννη, καλημέρα στον Κωνταντίνο και στον Χρήστο.
Ναι, για το φορτίο είδωλο δεν έχω κάτι να προσθέσω. Τα είπαν οι φίλοι.
Όσον αφορά το ερώτημα “πως θα αποδείξουμε ότι το δυναμικό είναι μηδέν σε κάθε σημείο της σφαίρας;”, η απάντηση που θα έλεγα ήταν, ότι αν σε ένα σημείο της σφαίρας Ζ, το δυναμικό δεν ήταν μηδέν, τότε μεταξύ των σημείων Α και Ζ θα υπήρχε διαφορά δυναμικού και θα είχαμε μετακίνηση ελευθέρων ηλεκτρονίων από το ένα σημείο στο άλλο.
Ενώ μιλάμε για σφαίρα σε στατικη ισορροπία. -
Να θυμίσω μια παλιότερη, πολύ μεγάλη συζήτηση, με παρόμοιο θέμα, του Πάνου Μουρούζη:
Έλξη ή άπωση;
Εκεί βέβαια η σφαίρα αρχικά ήταν φορτισμένη… -
Kαλημερα Διονύση. Το δυναμικο παντου πανω στο μεταλο το ξερουμε οτι ειναι μηδεν για τον λογο που ειπες. Ε μεις θελουμε να αποδειξουμε οτι το δυναμικο ειναι μηδεν στην νοητη σφαιρικη επιφανεια,μόνο λογω των φορτιων Q και του ειδωλου. Δεν υπαρχει μεταλο οταν βαζουμε το ειδωλο.Θελουμε να φτιαξουμε μια ισοδυναμικη επιφανεια ιδια με αυτην της επιφανειας της σφαιρας,χωρις ομως να υπαρχει σφαιρα,για να χρησιμοποιησουμε το θεωρημα της μοναδικοτητας.Τα παντα απο την νοητη σφαιρικη επιφανεια και εξω θα ειναι ιδια με το να ειχαμε την γειωμενη σφαιρα.
-
Καλημέρα σας.
https://i.ibb.co/V00Y9K61/page-0001-1.jpg -
Καλημέρα παιδιά.
Χρήστο πολύ σωστή λύση.
Διονύση έχεις δίκιο για την κατάσταση ισορροπίας.
Μια απόδειξη που χρησιμοποιεί τον Απολλώνιο κύκλο:
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 4 μέρες, 9 ώρες
Ο πεσσός και ο ιμάντας.
 Ένας οριζόντιος λαστιχένιος ιμάντας κινείται με σταθερή ταχύτητα 1,2 m/s. Ένας πεσσός κινείται στο επίπεδο του ιμάντα και μπαίνει κάθετα σ’ αυτόν με ταχ […]
Ένας οριζόντιος λαστιχένιος ιμάντας κινείται με σταθερή ταχύτητα 1,2 m/s. Ένας πεσσός κινείται στο επίπεδο του ιμάντα και μπαίνει κάθετα σ’ αυτόν με ταχ […]-
Το πρόβλημα αντλεί έμπνευση από το βιβλίο “200 More Puzzling Problems in Physics” χωρίς να αντιγράφει το πρόβλημα του βιβλίου ούτε στα νούμερα ούτε στα ζητούμενα.
Προστέθηκε η λανθασμένη λύση χάριν της αγάπης μου για το θέμα της ανεξαρτησίας των κινήσεων. -
Δεν κρατιέσαι όμως Γιάννη. Το σχόλιο σου στην ουσία δηλώνει ότι η λανθασμένη λύση είναι η δεύτερη 🙂
-
Καλησπέρα Γιάννη ,στην πρωτη λύση δεν μου φαίνεται ότι διέρχεται από το Δ λογω της μη σταθερής ταχύτητας του στο άξονα χ.
-
Κωνσταντίνε η αγάπη μου για την αρχή ανεξαρτησίας των κινήσεων μπορεί να εκληφθεί ότι η δεύτερη λύση είναι σωστή.
Το γιατί ψάχνουμε. -
Γιώργο και η y ταχύτητα μεταβάλλεται.
Το λάθος ας βρούμε. -
Το αρχικό πόνημα που έγραψα είχε πολλά.
Εξισώσεις ταχυτήτων, εξισώσεις τροχιάς, χρόνους….
Τόσο πολλά που ήταν άσχημο. Έτσι λογοκρίθηκε και έμεινε ένα ερώτημα και η ουσία του θέματος.
Και το πρόβλημα του βιβλίου είχε φασαρία και το διασκεύασα πάρα πολύ. -
Καλησπέρα Γιάννη.
Στο σύστημα του ιμάντα η τριβή δρα μόνο με βάση την σχετική ταχύτητα
και όχι ξεχωριστά για τα ux και uy.
άρα ολικό διάστημα s=(uσχ)2/2μg
Η προβολή αυτού του διαστήματος στην y διεύθυνση είναι το πλάτος του ιμάντα,
d=(uσχ)2/2μg Χ uy/ uσχ -
Καλησπέρα σας
Γιάννη, ωραίο θέμα!
Κάποια αποτελέσματα:
https://i.ibb.co/23v7qT8z/page-0001.jpg -
Γειά σου Άρη.
Αν κατάλαβα καλά προκρίνεις την πρώτη λύση μια και η υσχετ δεν είναι άλλη από τη V της πρώτης λύσης..
Μένει τότε να βρούμε το λάθος της δεύτερης λύσης. -
Γεια σου Χρήστο.
Ευχαριστώ.
Ποιο λάθος κάνει η δεύτερη λύση;
Γιατί η δεύτερη λύση δουλεύει άριστα στο ποτάμι, στην βολή και στην βολή με αντίσταση
-b.υ ; -
Χρήστο σωστό είναι αυτό (αν και πρέπει να εξηγήσουμε το γιατί έχει σταθερό μέτρο ώστε να χρησιμοποιήσουμε τύπους της ομαλά επιταχυνόμενης κίνησης).
Τότε όμως δεν θα ήταν η δεύτερη λύση αλλά μια τρίτη λύση.
Γιατί η “μέθοδος” της δεύτερης λύσης επιτυγχάνει σε μία περίπτωση βολής με αντίσταση -b.υ και εδώ αποτυγχάνει;
Η πρώτη λύση προφανώς είναι σωστή διότι ο παρατηρητής μας είναι αδρανειακός και δεν χρειάζεται κάποια δύναμη D’ Alembert. -
Γιαννη το λαθος της δευτερης λυσεως δεν ειναι μοναδικο. Λυνεις αλλη ασκηση. Εχεις αγνοησει την ταχυτητα του ιμαντα.Η ταχυτητα του ιμαντα αλλαζει την σχετικη ταχυτητα ιμαντα λιρας και αρα και την φορα της τριβης και αρα και την συνιστωσα της κατα την διευθυνση την καθετη στην κινηση του ιμαντα. Αρα το να αγνοησεις την ταχυτητα δεν ειναι σωστο. Aν ο ιμαντας κινειται πολυ γρηγορα,τοτε το απαιτουμενο πλατος μεγαλωνει πολυ. Εσυ μαλλον επιμενεις να το δικαιολογεις υπο το πρισμα καποιας αρχης με τιτλο “ανεξαρτησια των κινησεων” την οποια απ οτι νομιζω δεν εχεις καν διατυπωσει. Εκτος αν κανω λαθος.Μπορεις να διατυπωσεις με σαφη τροπο αυτο το θεωρημα το οποιο λες οτι σου αρεσει πολυ και το ονομαζεις αρχη ανεξαρτησιας των κινησεων,ετσι ωστε να καταλαβει καποιος ποτε μπορει να το εφαρμοζει και ποτε οχι;
-
Το λάθος της δεύτερης νομίζω είναι στο σημείο:
«Η κίνηση είναι επιβραδυνόμενη με την επιτάχυνση που βρήκαμε και πριν, την a=T/m=4m/s2»
Μα η α=4m/s2 έχει την διεύθυνση της Τ που με την σειρά έχει διεύθυνση V και φορά αντίθετη της V στο σύστημα του ιμάντα -
Η 2η λύση θέλει μια μικρή αλλαγή.
-
Καλημέρα Γιάννη, καλημέρα σε όλους.
Αν θέλουμε να δουλέψουμε με αρχή ανεξαρτησίας, θα πρέπει η μια κίνηση να μην επηρεάζει την άλλη. Εδώ λόγω της κίνησης του ιμάντα, κάθε στιγμή η ταχύτητα του πεσσού δεν είναι κάθετη στον ιμάντα, αλλά σχηματίζει γωνία θ με την κάθετη.
Η τριβή που αναπτύσσεται είναι αντίθετη της ταχύτητας αυτής, δεν είναι κάθετη στον ιμάντα όπως στη 2η λύση σου δίνεις.
Άρα η ταχύτητα του ιμάντα καθορίζει το μέτρο της επιτάχυνσης στην κάθετη διεύθυνση, δηλαδή η μια κίνηση καθορίζει την επιτάχυνση της άλλης… -
Καλημερα και απο εδω Διονυση.Συμφωνω με αυτο που λες.
“Εδώ λόγω της κίνησης του ιμάντα, κάθε στιγμή η ταχύτητα του πεσσού δεν είναι κάθετη στον ιμάντα, αλλά σχηματίζει γωνία θ με την κάθετη.
Η τριβή που αναπτύσσεται είναι αντίθετη της ταχύτητας αυτής, δεν είναι κάθετη στον ιμάντα” .
Αρα η επιταχυνση στην διευθυνση που ειναι καθετη στον ιμαντα δεν οφειλεται στην τριβη ολοκληρη, αλλα μονο σε μια συνιστωσα της. Στην δευτερη λυση ο Γιάννης την παιρνει ολοκληρη.Αυτο ειναι το λαθος.Μια απλη γεωμετρικη παρατηρηση αρκει. Δεν μου αρεσει η αναφορα σε καποιο θεωρημα το οποιο λεγεται αρχη ανεξαρτησιας των κινησεων το οποιο το βλεπω συνεχεια χωρις να εχω δει την διατυπωση του. -
Καλημέρα παιδιά και από εδώ.
Δίκιο έχετε σε όσα λέτε.
Θα επιχειρήσω να συνδέσω ή μάλλον διαφοροποιήσω τις δύο περιπτώσεις.
Την παρούσα με την κίνηση στον αέρα.
Όσα θα γράψω θα απηχούν τη δική μου θέση για το “τι εννοούμε με το κίνηση”. -
Καλησπέρα σας
Ένα συμπλήρωμα στην παραπάνω 1η ανάρτηση:
https://i.ibb.co/DHCkQ6Q5/P78-60-page-0001.jpg -
Μια Καρτεσιανή λύση:
Για τους οπαδούς της θέσης ότι δύο κινήσεις σημαίνει δύο συντεταγμένες. -
Γεια σου Γιάννη. Κάνε κοινόχρηστο το τελευταίο αρχείο.
-
Αποστόλη είναι τώρα εντάξει;
-
Γιάννη, ξαναδές το σχήμα:
https://i.ibb.co/J8kYMcH/2026-02-16-193327.png -
Ευχαριστώ Διονύση.
-
Διονύση σωστό είναι τελικά.
Η τριβή είναι αντίθετη της σχετικής ταχύτητας και όχι της ταχύτητας υx.
-
-
H/o Παναγιώτης Κουτσομπόγερας έγραψε ένα νέο άρθρο πριν από 4 μέρες, 12 ώρες
Μερική εξουδετέρωση μείγματος ασθενών βάσεων
 Αναμιγνύουμε τα παρακάτω 3 διαλύματα: Υ1: 400 mL διαλύματος αμίνης Α: R₁NH₂ 0,1 M Υ2: 200 mL διαλύματος αμίνης Β: R₂NH₂ 0,2 M Υ3: 400 mL διαλύμ […]
Αναμιγνύουμε τα παρακάτω 3 διαλύματα: Υ1: 400 mL διαλύματος αμίνης Α: R₁NH₂ 0,1 M Υ2: 200 mL διαλύματος αμίνης Β: R₂NH₂ 0,2 M Υ3: 400 mL διαλύμ […]-
Καλησπέρα Παναγιώτη. Η συγκέντρωση του HCl δεν χρειάζεται ή ξέχασες να τη γράψεις;
-
Καλησπερα Θοδωρή, είναι εμμέσως ζητούμενη για το pH αργοτερα – δινονται το ποσοστα (%) των βάσεων RNH₂ που αντέδρασαν
-
Καλησπερα Δημητρη, για σταδιακη εισαγωγη στην ασκηση και περαιτερω εξοικειωση με τους λογαριθμους
-
Παναγιώτη καλησπέρα. Γιατί ζητάς το pH αφού δίνεις τη συγκέντρωση των ΟΗ;
Επίσης, το ποσοστό που δίνεις για τις βάσεις, σε τι αφορά; Στην αντίδραση με το HCl ή στο συνολικό φαινόμενο και με τους ιοντισμούς; Δεν είναι ξεκάθαρο τι ακριβώς έχουμε ως δεδομένο. -
ΑΠΑΝΤΗΣΕΙΣ:
1. pH τελικού διαλύματος (πρώτη ανάμιξη)
pH = 10,7
2. Σταθερά Kb(R₁NH₂)
Kb1 = 4 * 10⁻⁴
3. Σταθερά Kb(R₂NH₂)
Kb2 = 6,25 * 10⁻⁴
4. pH διαλύματος Υ3
pH = 1
5. Συντακτικοί Τύποι (Σ.Τ.) των αμινών
Αμίνη Α: CH₃NH₂
Αμίνη Β: CH₃CH₂NH₂
6. Ευκολότερη υγροποίηση
Η αμίνη Β (CH₃CH₂NH₂), λόγω μεγαλύτερης σχετικής μοριακής μάζας – ισχυρότερων δυνάμεων London.
7. pH μετά την προσθήκη 800 mL Υ3 και συμπύκνωση στο 1 L
pH = 5,9 -
Δημητρη καλησπερα, το ποσοστό (%) της βάσης RNH₂ αναφερεται στην αντιδραση με το HCl – ιοντισμο δεν θα ειχαμε ουτως ή άλλως;
-
Παναγιώτη καλησπέρα. Αναρτώ τις απαντήσεις μου. Αυτή είναι η πρώτη σελίδα:
-
και αυτή είναι η δεύτερη. Έχουμε μια μικρή διαφορά στο τελευταίο ερώτημα.
Η ερώτησή μου Παναγιώτη αφορά στο εξής. Για να λύσουμε την άσκηση θεωρούμε ότι έχουμε δύο ρυθμιστικά και οι συγκεντρώσεις τους είναι αυτές που προκύπτουν από τις αντιδράσεις με το HCl. Ωστόσο, όπως φάνηκε στη συζήτηση για τα οξέα, μπορούμε να θεωρήσουμε ότι γίνονται επιπλέον αντιδράσεις. Οπότε προφανώς το ποσοστό αλλάζει (έστω και κατά πολύ λίγο). Αλλά μάλλον δεν έχει ιδιαίτερο ενδιαφέρον το τόσο πολύ σκάλισμα. Και πάλι συγχαρητήρια για τις ασκήσεις σου. -
Παναγιώτη και Δημήτρη καλησπέρα.
Παναγιώτη συγχαρητήρια για τις όμορφες ασκήσεις ιοντικής που ανεβάζεις. Μια παρατήρηση μόνο σχετικά με τις προσεγγίσεις. Στην 2η αμίνη (αιθυλαμίνη) Kb/C= 0.0156 > 0.01. Δεν ασχολήθηκα βέβαια να υπολογίσω το σφάλμα που προκύπτει.
Δημήτρη συμφωνώ με τα αποτελέσματα που έβγαλες, εκτός από το 7ο . Εμένα μου βγαίνει (x+c)^2=1.64*10^-12, x+y=ρίζα1,64*10^-6 και ph=6-0.107=5.89 -
Καλησπερα Δημητρη και Ανέστη κι ευχαριστω για τον χρονο και τα σχολια σας – δικο μου λαθος για το 7ο ερωτημα, πρέπει να δωσω οτι log164=2,2 οποτε το pH βγαινει 5,9.
1. Υπολογισμός moles
· Αμίνη Α (R1NH2): n = C * V = 0,1 M * 0,4 L = 0,04 mol.
· Αμίνη Β (R2NH2): n = C * V = 0,2 M * 0,2 L = 0,04 mol.
· HCl (από το Υ3): n = C * V = 0,1 M * 0,8 L = 0,08 mol.
2. Αντίδραση Εξουδετέρωσης
Προσθέτοντας το HCl, οι δύο βάσεις αντιδρούν πλήρως:
R1NH2 + HCl -> R1NH3Cl
R2NH2 + HCl -> R2NH3Cl
Συνολικά moles βάσεων = 0,04 + 0,04 = 0,08 mol.
Moles HCl = 0,08 mol.
Επειδή τα moles είναι ίσα, έχουμε πλήρη εξουδετέρωση. Στο διάλυμα υπάρχουν μόνο τα άλατα των αμινών (τα συζυγή τους οξέα R1NH3+ και R2NH3+).
3. Συγκεντρώσεις και Σταθερές (στο 1 L)
· Συγκέντρωση άλατος Α (C1): 0,04 mol / 1 L = 0,04 M.
· Συγκέντρωση άλατος Β (C2): 0,04 mol / 1 L = 0,04 M.
· Σταθερά Ka1: Kw / Kb1 = 10^-14 / (4 * 10^-4) = 2,5 * 10^-11.
· Σταθερά Ka2: Kw / Kb2 = 10^-14 / (6,25 * 10^-4) = 1,6 * 10^-11.
4. Υπολογισμός [H3O+]
Για μείγμα δύο ασθενών οξέων:
[H3O+] = ρίζα( Ka1C1 + Ka2C2 )
[H3O+] = ρίζα( 2,510^-11 * 0,04 + 1,610^-11 * 0,04 )
[H3O+] = ρίζα( 0,04 * (2,510^-11 + 1,610^-11) )
[H3O+] = ρίζα( 0,04 * 4,1 * 10^-11 )
[H3O+] = ρίζα( 0,164 * 10^-11 ) = ρίζα( 1,64 * 10^-12 )= ρίζα( 164 * 10^-14 )
5. Υπολογισμός pH
pH = 7 – 2,2/2
pH = 5,9Ανεστη σωστη η παρατηρηση σου επισης – μου διεφυγε – θα αλλαχτει, ισως και με το ΕΚΙ να μειωθει εντος οριων ο βαθμος ιοντισμου της αμινης, ευχαριστω πολυ και παλι για τις ορθες παρατηρησεις σας
-
Τελικά το έκανα το αριθμητικό. Έχω γράψει 5/8 Χ 10^-4 αντί του σωστού 5/8Χ10^-3.
-
Παναγιώτη καλησπέρα και πάλι. Όντως λόγω ΕΚΙ το y θα μικρύνει και το σφάλμα τελικά είναι πολύ μικρό. Απλώς μπορεί να προβληματίσει τους μαθητές
-
Καλημέρα κύριε Κουτσομπόγερα. Μια ενδεικτική λύση και από εμένα, με κάποιες επισημάνσεις, σχετικά με την εκφώνηση.
Με βάση τους πίνακες τιμών έχουμε:
(ποσότητα/mol) R1NH2+ HCl→ R1NH3Clαντ./παρ. χ χ χκαι(ποσότητα/mol) R2NH2+ HCl→ R2NH3Clαντ./παρ. ψ ψ ψΑπό Υ1: nR1NH2=0,1M∙400 mL=0,04 mol. Γνωρίζουμε ότι το κλάσμα εξουδετέρωσης της R1NH2 είναι ίσο με 4/9 από το ποσοστό εξουδετέρωσης που είναι (400/9)%, άρα 4/9 =χ/0,04 => 9χ=0,16=>χ=0,8/45 (1)
Από Υ2: nR2NH2=0,2M∙200 mL=0,04 mol. Γνωρίζουμε ότι το κλάσμα εξουδετέρωσης της R2NH2 είναι ίσο με 5/9 από το ποσοστό εξουδετέρωσης που είναι (500/9)%, άρα 5/9 =ψ/0,04 => 9ψ=0,2=>ψ=1/45 (2)
Τότε nHCl=(1,8/45)mol=0,04mol και CHCl=[(0,04 /0,4]M=0,1M .
Έτσι pΗ(Y3)=1. Αφού HCl +Η2Ο→ Η3Ο+ +Cl-Για το Υ2: m=n∙Mr g/mol => 1,8=0,04∙Mr =>Mr=45.
Αφού η CH3NH2 έχει Mr=31 η R2NH2 με Mr=31+14= 45 θα είναι η CH3CΗ2NH2.
Μετά την ανάμειξη στο διάλυμα υπάρχουν δύο άλατα , τα οποία διίστανται, οπότε προκύπτουν δύο ρυθμιστικά διαλύματα το (CH3CΗ2NH2/ CH3CΗ2NH3+) και το (R1NH2/ R1NH3+), για τα οποία ισχύει:Ι. Κb((R1NH2)=[OH-][ R1NH3+]/[ R1NH2] => Κb((R1NH2)=5∙10-4∙χ/0,04-χ =>
Κb((R1NH2)= 5∙10-4∙χ/ψ=5∙10-4∙(0,8/45)∙45=4∙10-4
ΙΙ. Κb((R2NH2)=[OH-][ R2NH3+]/[ R2NH2] => Κb((R2NH2)=5∙10-4∙ψ/0,04-ψ =>
Κb((R2NH2)= 5∙10-4∙ψ/χ=5∙10-4∙(1/45)∙45/0,8=6,25∙10-4
H R2NH2 είναι η CH3CΗ2NH2 ( αιθυλαμίνη) και η R1NH2 , ως ασθενέστερη της CH3CΗ2NH2 είναι η CH3NH2 (μεθυλαμίνη)- Αρχικά είναι λίγο δύσκολο στα Υ1 και Υ2 να προσθέσουμε 800 mL Y3, γιατί αυτό που δίνεται είναι: << Υ3: 400 mL διαλύματος HCl >> Θα μπορούσε στο διάλυμα που προκύπτει μετά την ανάμειξη να διαβιβάσουμε 896 cm3 αέριου υδροχλωρίου , μετρημένα σε STP συνθήκες ,που είναι 0,04 mol. Ο όγκος του νέου διαλύματος θα παρέμενε 1 L, χωρίς να χρειάζεται να γίνει συμπύκνωση. Αλήθεια ποιος βεβαιώνει ότι με την συμπύκνωση, μαζί με την απομάκρυνση νερού ΔΕΝ απομακρύνεται και ποσότητα αμίνης;;;
Καταλήγουμε στην ίδια κατάσταση αν δημιουργούσαμε διάλυμα 1L , που αρχικά περιείχε, 0,04 mol CH3NH2 , 0,04 mol CH3CH2NH2 και 0,08 mol HCl.
Έτσι με βάση τους πίνακες τιμών έχουμε:
(ποσότητα/mol) CH3NH2 + HCl→ CH3NH3Clαντ./παρ. 0,04 0,04 0,04και(ποσότητα/mol) CH3CH2NH2 + HCl→ CH3CH2NH3Clαντ./παρ. 0,04 0,04 0,04 Τα δύο άλατα διίστανται και τα παραγόμενα ιόντα CH3NH3+ και CH3CΗ2NH3+ με συγκέντρωση 0,04Μ το καθένα, ιοντίζονται. Έτσι έχουμε:
(C/M) CH3NH3+ +H2O ⇄ CH3NH2 +H3O+ιοντ./παρ. φ φ φκαι (C/M) CH3CH2NH3+ +H2O ⇄ CH3CH2NH2 + H3O+
ιοντ./παρ. ω ω ω Οπότε: [CH3NH3+]=(0,04-φ), [CH3NH2]=φ, [H3O+]=φ +ω
[CH3CH2NH3+]= 0,04- ω και [CH3CH2NH2] =ω.
Όμως :Κw=Ka,1∙ Kb,1 => Kb,1=2,5∙10-11 και Κw=Ka,2∙ Kb,2 => Kb,2=1,6∙10-11
Kb,1=[H3O+][CH3NH2]/ [CH3NH3+] =>2,5∙10-11∙(0,04-φ)=φ∙(φ + ω)
Έστω φ<< 0,04 τότε 10-12 = φ∙(φ + ω) (1)
Kb,2=[H3O+][ CH3CH2NH2]/ [CH3CH2NH3+] =>1,6∙10-11∙(0,04-ω)=ω∙(φ + ω)
Έστω ω<< 0,04 τότε 0,64∙10-12 = φ∙(φ + ω) (2)
(1) +(2) : 1,64∙10-12=(φ + ω) ∙(φ + ω) => [H3O+]=√164∙10-7 ***
pΗ=7- 0,5log164=7-1,1=5,9.
Αφού οι θετικοί αριθμοί φ και ω έχουν άθροισμα φ +ω= √164∙10-7 οι υποθέσεις φ<< 0,04 και ω<< 0,04 είναι αποδεκτές. -
Καλημερα σας, μια χαρα μπορουμε να προσθεσουμε το διαλυμα των 800 mL αν τα διαλυματα των 400 mL και 200 mL έχουν τοποθετηθεί σε μεγαλύτερο δοχείο, επισης μετα την αναμειξη των ουσιων αυτων ΔΕΝ υπαρχει αμινη παρα μονο 2 αλατα με υψηλα σημεια ζεσεως (αποσυντιθενται με θερμανση ακριβεστερα) αρα και παλι κανενα προβλημα
-
Άφησα απ’ έξω το ερώτημα < Ποια από τις δύο αμίνες υγροποιείται πιο εύκολα στις ίδιες συνθήκες πίεσης;>
Αρχικά για να κάνουμε υγροποίηση πρέπει οι αμίνες να είναι σε αέρια κατάσταση έχοντας ορισμένη θερμοκρασία και ασκώντας συγκεκριμένη πίεση. Η υγροποίηση μπορεί να γίνει διατηρώντας σταθερή τη θερμοκρασία και αυξάνοντας την πίεση. Επειδή έχουμε κατά την εκφώνηση << ίδιες συνθήκες πίεσης>> πρέπει η πίεση να είναι ίση και στις δύο περιπτώσεις. Τότε ποια υγροποιείται πιο εύκολα;
Η υγροποίηση μπορεί να γίνει διατηρώντας σταθερή την πίεση και μειώνοντας τη θερμοκρασία. Αυτό θα γίνει με ψύξη, αποσπώντας ένα ποσό θερμότητας. Προφανώς υγροποιείται πιο εύκολα αυτή πού απαιτεί να αποσπαστεί λιγότερο ποσό θερμότητας. Πως γίνεται ο υπολογισμός του; Από τον νόμο της θερμιδομετρίας (Q=cmΔθ) [είναι εκτός ύλης] Πέρα από αυτό, χωρίς να είναι κανένα μέγεθος γνωστό , παρά μόνο μια ανισωτική σχέση μεταξύ Δθ(1) και Δθ(2) τι υπολογισμοί να γίνουν;;;
Ας υποθέσουμε ότι το ζητούμενο ήταν η σχέση μεταξύ των σημείων βρασμού σε ίδια πίεση. Τότε προφανώς και στα δύο υγρά αναπτύσσονται διαμοριακές δυνάμεις, που είναι οι δυνάμεις London και ο δεσμός υδρογόνου. Από όσα γράφονται στο βιβλίο της χημείας ,Γ-Λυκείου η ενέργεια διάσπασης /ποσότητα για τις δυνάμεις London είναι από 0,1 KJ/mol έως 10 KJ/mol ενώ για τον δεσμό υδρογόνου είναι από 10 KJ/mol έως 40 KJ/mol. Πώς είναι δυνατόν να εξετάζουμε την διαφοροποίηση μεταξύ των δυνάμεων London και όχι μεταξύ των δυνάμεων του δεσμού υδρογόνου;;;;;; -
σχετικα με το ερωτημα:
Μεταξύ μεθυλαμίνης (CH₃NH₂) και αιθυλαμίνης (CH₃CH₂NH₂), πιο εύκολα υγροποιείται η αιθυλαμίνη.
Αιτιολόγηση (μοριακές δυνάμεις):
Και οι δύο είναι πρωτοταγείς αμίνες και μπορούν να σχηματίζουν δεσμούς υδρογόνου (Ν–Η···Ν). Επομένως, η βασική διαφορά στη θερμοκρασία υγροποίησης δεν οφείλεται στο είδος των διαμοριακών δεσμών αλλά στην έντασή τους.
Η αιθυλαμίνη έχει:μεγαλύτερη σχετική μοριακή μάζαμεγαλύτερη ανθρακική αλυσίδαμεγαλύτερη πολωσιμότητα⇒ άρα εμφανίζει ισχυρότερες δυνάμεις London (διασποράς) μεταξύ των μορίων της.
Οι ισχυρότερες συνολικές διαμοριακές δυνάμεις σημαίνουν:υψηλότερο σημείο ζέσεωςευκολότερη υγροποίηση στην ίδια πίεσηΣυγκεκριμένα, η αιθυλαμίνη έχει υψηλότερο σημείο ζέσεως από τη μεθυλαμίνη, άρα υγροποιείται ευκολότερα.
Συμπέρασμα:
Η αιθυλαμίνη υγροποιείται πιο εύκολα, επειδή έχει ισχυρότερες διαμοριακές δυνάμεις λόγω μεγαλύτερου μεγέθους μορίου.Oι μαθητες ειναι μια χαρα ικανοι να απαντησουν ετσι – οτι αλλο αναφερετε μπερδευει χωρις λογο κατα την γνωμη μου
-
-
H/o Ανδρέας Ριζόπουλος έγραψε ένα νέο άρθρο πριν από 4 μέρες, 16 ώρες
Δυο πειράματα με δακτύλιους
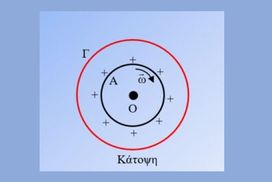 Πείραμα 1ο Όπως φαίνεται στην κάτοψη του διπλανού σχήματος, δύο ομόκεντροι δακτύλιοι, Α από μονωτικό υλικό και Γ από μέταλλο, τοποθετούν […]
Πείραμα 1ο Όπως φαίνεται στην κάτοψη του διπλανού σχήματος, δύο ομόκεντροι δακτύλιοι, Α από μονωτικό υλικό και Γ από μέταλλο, τοποθετούν […]-
Καλό μεσημέρι Ανδρέα.
Προχωρημένα περιβάλλοντα έχει το σημερινό μενού!
Βλέπω προχωράτε στην επαγωγή… -
Γεια σου Ανδρέα, ωραίος ο τρόπος να δημιουργηθεί μεταβαλλόμενο ρεύμα και ΗΕΔ από επαγωγή.
-
Καλημέρα συνάδελφοι. Ευχαριστώ για τα σχόλια.
Διονύση έτσι όπως έχει γίνει πλέον το σχολείο, δεν ξέρουμε κάθε βδομάδα πόσες ώρες θα χαθούν για διάφορες δράσεις, οπότε προχωράμε και βλέπουμε…
Παύλο ήθελα δυο διαφορετικούς τρόπους μεταβολής ροής στο ίδιο πρόβλημα, για να συγκρίνουν οι μαθητές. -
Καλησπέρα Ανδρέα και συγχαρητήρια για την άσκηση!!
Απαιτείται παραγωγική και συνθετική σκέψη ,κάτι που…ξεχωρίζει την ήρα από το στάρι.
Πρέπει να υπάρχει κάποιο τέτοιο θέμα στις πανελλήνιες.
Νάσαι καλά.
-
-
H/o Αποστόλης Παπάζογλου έγραψε ένα νέο άρθρο πριν από 4 μέρες, 17 ώρες
Πώς θα κινηθεί η ράβδος;
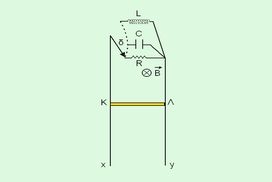 Δύο κατακόρυφοι μεταλλικοί αγωγοί χωρίς αντίσταση απέχουν απόσταση d και βρίσκονται σε οριζόντιο ομογενές μαγνητικό πεδίο, κάθετο στο επίπεδο των αγωγών, μ […]
Δύο κατακόρυφοι μεταλλικοί αγωγοί χωρίς αντίσταση απέχουν απόσταση d και βρίσκονται σε οριζόντιο ομογενές μαγνητικό πεδίο, κάθετο στο επίπεδο των αγωγών, μ […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 4 μέρες, 21 ώρες
Κλείνοντας έναν – έναν τους διακόπτες.
 Στο κύκλωμα του διπλανού σχήματος, οι διακόπτες είναι ανοικτοί, τα όργανα ιδανικά, ενώ δίνονται για την πηγή, ΗΕΔ Ε=20V και r=2Ω, ενώ οι δυο αντιστάτε […]
Στο κύκλωμα του διπλανού σχήματος, οι διακόπτες είναι ανοικτοί, τα όργανα ιδανικά, ενώ δίνονται για την πηγή, ΗΕΔ Ε=20V και r=2Ω, ενώ οι δυο αντιστάτε […]-
Γεια σου Διονύση πολύ όμορφη και χρήσιμη ανάρτηση. Με μια άσκηση μελετάς πως επηρεάζει ενα κύκλωμα το κλείσιμο του διακόπτη σε συνδυασμό και με βραχυκύκλωμα.
-
Καλημέρα Παύλο και καλή Κυριακή.
Σε ευχαριστώ για το σχολιασμό και χαίρομαι που σου άρεσε. -
Καλημέρα Διονύση, τώρα που πέρασε το “εορταστικό” τριήμερο, όλοι οι “αναξιοπαθούντες” , vegan, προληπτικοί, μη-“ερωτευμένοι”, αναμένοντας
το αποκριάτικο “ξεφάντωμα”…. απολαμβάνουν φυσική, main stream και alternativeΑν και στην προσωπική ζωή οι επιλογές μου ήταν σχεδόν πάντα alternative, στην
φυσική προτιμώ main stream επιλογές…Μία τέτοια είναι και η παραπάνω ανάρτησή σου, με ουσιαστικό διδακτικό αποτύπωμα.
Συμπληρώνω κάτι που ξέχασες να γράψεις
ι) όταν (δ1) κλειστός, η ισχύς της πηγής Pηλ=EI(2)=80W,
ii) όταν (δ1) και (δ2) κλειστοί, η ισχύς της πηγής Pηλ=EI(β)=200W
Θα πρόσθετα ως ερώτημα,
“σε ποια από τις τρεις περιπτώσεις η πηγή αποδίδει στο φορτίο των 3C συντομότερα, την ενέργεια που υπολογίστηκε”
Ελπίζοντας σε ένα repeat της χθεσινής νίκης-εμφάνισης και στο βασικό οπαδικό άθλημα στη συμπρωτεύουσα
-
Καλό μεσημέρι Θοδωρή και σε ευχαριστώ για το σχόλιο και την… υπενθύμιση!
Το ερώτημα που πρότεινες το πρόσθεσα, στο τέλος…
-
-
H/o Χρήστος Αγριόδημας έγραψε ένα νέο άρθρο πριν από 5 μέρες, 6 ώρες
Παράλληλα επιβραδύνεται, σε σειρά επιταχύνεται…
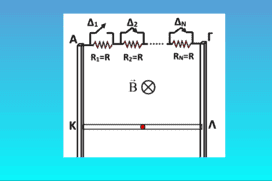 Ένας ομογενής αγωγός ΚΛ μήκους ℓ, μάζας m και μηδενικής ωμικής αντίστασης βρίσκεται σε επαφή με δύο κατακόρυφους μεταλλικούς οδηγούς Ay1 και Γy2 που έχο […]
Ένας ομογενής αγωγός ΚΛ μήκους ℓ, μάζας m και μηδενικής ωμικής αντίστασης βρίσκεται σε επαφή με δύο κατακόρυφους μεταλλικούς οδηγούς Ay1 και Γy2 που έχο […]-
Δεν είναι στα πλαίσια εξετάσεων, αλλά έχει την πλάκα της.
-
Καλημέρα Χρήστο και καλές απόκρηες!
Τι έφτιαξες!!!
Αν δεν είχαμε Ν διακόπτες αλλά 2, δεν θα ήταν και θέμα εξετάσεων; -
Καλημέρα Διονύση, καλές απόκριες.
Το εχω ήδη έτοιμο με δύο αντιστάσεις σαν β θεμα. ..
Θα δημοσιευθεί και εδω ή σε διαγωνισμα αν μπει ή μονο του. -
Καλημέρα, πολύ ωραία ανάλυση Χρήστο!
-
Σε ευχαριστώ Παύλο.
Να σαι καλά -
Καλησπέρα Χρήστο. Πολύ δουλειά! Μετά από αυτήν την άσκηση, το θέμα “κλείνει ο διακόπτης” έκλεισε. Η light έκδοση με δυο διακόπτες θα είναι καλό β΄ θέμα, πιο μαθητικό, οπότε την αναμένουμε.
-
Αντρέα καλησπέρα.
Σε ευχαριστώ για το σχόλιο. Να σου πω την αλήθεια και εγώ προτιμώ την πιο απλή διάταξη.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 6 μέρες, 5 ώρες
Η κλίση της σιδηροτροχιάς.
 Θέλουμε το τραινάκι να πάει στον συντομότερο χρόνο από το Α στο Β. Τριβές και αντιστάσεις αέρα δεν έχουμε. Η καλύτερη επιλογή θα ήταν φυ […]
Θέλουμε το τραινάκι να πάει στον συντομότερο χρόνο από το Α στο Β. Τριβές και αντιστάσεις αέρα δεν έχουμε. Η καλύτερη επιλογή θα ήταν φυ […]-
Kαλημερα Γιάννη. Μου θυμισε διαθλαση με οριακη γωνια πηγαινοντας απο πυκνο μεσο σε αραιο μεσο. Ομως παιρνοντας την μεση ταχυτητα στο κεκλιμενο κομματι κανω εναν υπολογισμο και βρισκω οτι ο δεικτης διαθλασης εξαρταται απο την γωνια. Εκει σταματησα 🙂
-
Καλημέρα Κωνσταντίνε.
Το βρήκες. Αυτό είναι.
https://i.ibb.co/zT8QCY01/Screenshot-1.png -
Αν δεν θέλουμε να εμπλέξουμε το φως:
https://i.ibb.co/39FKWtTc/41.pngΤότε όμως είναι άσχημη λύση.
-
Καλημέρα Γιάννη. Δες αυτό:https://i.ibb.co/0yn7NmDv/feb-95.png
-
Καλημέρα Γιώργο
Πολύ σωστή. -
Γιαννη αρχικα εκανα ενα λαθακι σε μια πραξη. Ειναι θ=Αrcsin(<υ>/υmax)=Αrcsin(1/2)=π/6 .Δεν σκεφτηκα να αναφερθω σε καποιο θεωρημα. Οταν η μεταβολη της ταχυτητας ειναι γραμμικη, το 1/2 ειναι προφανες.
-
Κωνσταντίνε αν μου έδιναν την άσκηση πριν μια μέρα θα έπιανα επίσης χαρτί και μολύβι και θα δούλευα με παραγώγους (όπως στην προηγούμενη λύση και στη λύση του Γιώργου). Τα λάθη είναι πιθανό να συμβούν.
Καταλαβαίνουν όλοι οι φίλοι ότι πρόκειται για ένα καλαμπούρι.
Μια απρόσμενη σύνδεση της αρχής Ήρωνος – Φερμά με ένα άσχετο με το φως φαινόμενο.
Ανάλογο:
https://i.ibb.co/HTSMFTvr/Screenshot-1.png
Ο νεαρός κινείται στον δρόμο με διπλάσια ταχύτητα απ’ ότι στο χωράφι.
Πως πρέπει να κινηθεί ώστε να προλάβει το αργότερο από αυτόν κάρο στο συντομότερο χρόνο; -
Καλησπέρα σας
Γιάννη, όμορφο πρόβλημα!
https://i.ibb.co/JhdG82Z/page-0001.jpg -
Μπράβο Χρήστο!!
Δεν θα σκεφτόμουν το σημείο Φερμά με τίποτα. -
Και μια δευτερη λυση ,πιο εύκολη . που καταληγει στην ίδια τελικη συναρτηση πολυ πιο γρηγορα.https://i.ibb.co/XfqDpnNS/feb-96.png
-
Μια ακόμη:
https://i.ibb.co/Y4RFstyh/2-page-0001.jpg -
Καλησπέρα Γιώργο και Χρήστο.
Εμπλουτίζετε πολύ το σύνολο των λύσεων!
Ευχαριστώ. -
Συμπλήρωμα της 1ης λύσης.
Απόδειξη χωρίς τριγωνομετρία:
https://i.ibb.co/4w4kYm2X/3-page-0001.jpg -
Καλημέρα Χρήστο.
Μου αρέσει ακόμα περισσότερο με την τελευταία τροποποίηση.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 6 μέρες, 21 ώρες
Άλλη μια ισορροπία αγωγού.
 Ο ευθύγραμμος αγωγός ΑΔ του σχήματος έχει μάζα m=0,4kg, μήκος l=0,8m και κρέμεται κατακόρυφα από δύο ελατήρια, με το ίδιο φυσικό μήκος. Ό […]
Ο ευθύγραμμος αγωγός ΑΔ του σχήματος έχει μάζα m=0,4kg, μήκος l=0,8m και κρέμεται κατακόρυφα από δύο ελατήρια, με το ίδιο φυσικό μήκος. Ό […]-
Σαράντα++ μάλλον πενήντα – χρόνια φούρναρης ξέρεις πως με απλά υλικά να φτιάχνεις ζυμωτό ψωμί, τέτοιο ώστε …. να τρώει ο πατέρας και του παιδιού να μην δίνει….
Προφανώς αναφέρομαι στο (iv) ερώτημα και στη διερεύνηση που κάνειςΕυχαριστούμε
-
Καλημερα Διονυση. Ωραια ασκηση μηχανικης με ολιγον απο δυναμη Laplace. Eνα ερωτημα που ισως θα μπορουσε να κανει ενας μαθητης ειναι πως ξερουμε οτι η δυναμη Laplace εφαρμοζεται στο μεσον το αγωγου.Η εξηγηση ειναι μεν απλη αλλα δεν θυμαμαι αν το σχολικο γραφει κατι επ αυτου.
-
Καλημέρα Θοδωρή, καλημέρα Κωνσταντίνε και σας ευχαριστώ για το σχολιασμό.
Θοδωρή, αν λάβεις υπόψη σου ότι από το 2ο έτος του πανεπιστημίου, έκανα ιδιαίτερα μαθήματα, πέρασα πια τα 50 χρόνια!!!
Βέβαια συμπληρώνω 12 χρόνια, που έχω σταματήσει κάθε είδους διδασκαλία… Οπότε δεν ξέρω αν πρέπει να κάνουμε αφαίρεση…
Κωνσταντίνε, με μια πρώτη ματιά στο σχολικό, βλέπω να έχεις δίκιο!!!
Δεν βρήκα να γράφει κάτι για το σημείο εφαρμογής της δύναμης Laplace…
Ίσως επειδή, όταν γράφονταν τα βιβλία, οι συγγραφείς ήξεραν ότι όλοι οι μαθητές θα διδάσκονταν στη γ.π. τα βασικά του ηλεκτρομαγνητισμού.
Έτσι στη φυσική της γενικής παιδείας διαβάζουμε:https://i.ibb.co/b5Yy7pCM/aa.png
Κόψε από εδώ, άλλαξε το άλλο, τροποποίησε το τρίτο, άντε να μην δημιουργούνται κενά και να μπορεί να υπάρξει σοβαρή διδασκαλία…
-
Καλησπέρα Διονύση. Πολύ καλή για επανάληψη. Η Laplace είναι ένα μικρό μέρος της ανάρτησης, στην οποία κυριαρχεί η ισορροπία στερεού, με το 4ο ερ΄ωτημα εξαιρετικό.
Σε αυτό που λέει τώρα ο Κωνσταντίνος, ας σκεφτούμε πόσες ασκήσεις κυκλοφορούν με τμήμα αγωγού εντός πεδίου, που η επίσημη θεωρία δεν υποστηρίζει!
Αν θεωρήσουμε ότι η Φυσική Γενικής το καλύπτει, γιατί να μην είναι στην ύλη π.χ. και οι πυκνωτές; -
Καλησπέρα Διονύση
Εξαιρετική ασκηση και βέβαια το 4ο ερώτημα είναι ο πρωταγωνιστής.
Θοδωρή όσα χρόνια και αν περάσουν άλλα τα μάτια του λαγού… -
Καλημέρα Ανδρέα, καλημέρα Χρήστο και καλό ΣΚ.
Σας ευχαριστώ για το σχολιασμό.
ΥΓ
Γιορτάζετε σήμερα; Να ευχηθώ χρόνια πολλά!!! -
Καλημέρα Διονύση,, ρωτάς για τα τελευταία 12 χρόνια;
Με 4500 αναρτήσεις και όσα έχεις “υποφέρει” από διάφορους “επιστήμονες”,
όχι μόνο μετράνε, αλλά είναι “βαρέα και ανθυγειανά”Επίσης, σήμερα νομίζω πως “γιορτάζουν” όλοι
-
Καλό μεσημέρι Θοδωρή.
Πετυχημένο σύνθημα…
-
-
H/o Παναγιώτης Κουτσομπόγερας έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα
Μερική εξουδετέρωση μείγματος ασθενών οξέων
 ΕΚΦΩΝΗΣΗ 1 Αναμιγνύονται τα παρακάτω 3 διαλύματα: 500 mL διαλύματος CH3COOH 0,1 M 200 mL διαλύματος HCOOH 0,25 M 100 mL διαλύματος NaOH […]
ΕΚΦΩΝΗΣΗ 1 Αναμιγνύονται τα παρακάτω 3 διαλύματα: 500 mL διαλύματος CH3COOH 0,1 M 200 mL διαλύματος HCOOH 0,25 M 100 mL διαλύματος NaOH […]-
Παναγιώτη καλησπέρα. Στα άδυτα της ιοντικής! Βρήκα pH=4 και (100/6)%. Οπότε μπορούμε να πούμε κατευθείαν ότι το ποσοστό του άλλου οξέος, του HCOOH, που αντέδρασε είναι (500/6)%. Αυτό δεν ισχύει πάντα όμως, έτσι; Δηλαδή το άθροισμα των δύο ποσοστών να είναι 100%.
-
Θοδωρη ταχυτατος, μπραβο (και ηθελα να κανω αλλαγες …κλαψ) νομιζω οτι αλγεβρικα και χημικα πρεπει το άθροισμα των δύο ποσοστών να είναι 100%.
-
Έχει πέσει ανάλογη το 2020 στις επαναληπτικές πανελλαδικές του παλαιού συστήματος!! Είναι πλεόν λίγο (έως πολύ) too much νομίζω!
-
ακριβως (ειναι too much, αλλα happy brainwork!) – κι εγω απο εκει την θυμηθηκα
-
Νομίζω Παναγιώτη ότι το άθροισμα των ποσοστών δεν είναι πάντα 100%. Είναι μόνο όταν η βάση είναι σε στοιχειομετρική αναλογία με καθένα από τα δύο οξέα.
-
αν υπολογισεις και το ποσοστο του HCOOH εδω νομιζω ειναι 5/6 (αν εχω καταλαβει τι εννοεις)
-
Επειδή το’χα ψάξει παλαιότερα, με αφορμή την ερώτηση μιας μαθήτριας!!, θυμάμαι ότι όταν τα αρχικά mol της βάσης είναι σε στοιχειομετρική αναλογία με τα αρχικά mol κάθε οξέος, όπως εδώ που είναι 1:1 με κάθε οξύ, αφού τα αρχικά mol όλων είναι 0,05, τότε ισχύει ότι το άθροισμα είναι 100%. Αν όμως τα mol της βάσης δεν ήταν 0,05 αλλά π.χ. 0,07, τότε το άθροισμα δεν είναι 100%.
-
Καλησπέρα Θοδωρή, πολύ σωστή η παρατήρηση σου
-
Έτσι θυμάμαι. Αν το δοκιμασουμε θα το επιβεβαιώσουμε. Απλά τώρα βαριέμαι να μπω σε πράξεις.
-
Καλημέρα κύριε Κουτσομπόγερα.
Ενδεικτική απάντηση: (και για τις δύο εκφωνήσεις)
Αρχικά n(HCOOH)= n(CH3COOH)= n(NaOH)=0,05mol=n mol.
(ποσότητα/mol) CH3COOH + NaOH →CH3COONa +H2O
αρχικά n n
αντ./παρ. x x x
Μένουν n-x n-x x
και
(ποσότητα/mol) HCOOH + NaOH → HCOONa +H2O
αρχικά n n-χ
αντ./παρ. n-x n-x n-x
τελικά x – n- x
C(CH3COOH)= C(HCOONa)=[(n-x)/V]M=C1M και C(CH3COOΝα)= C(HCOOΗ)=[χ/V]M=C2M(συγκέντρωση/Μ) CH3COOΝα(aq) → CH3COO-(aq) + Na+(aq)
διίστ./παρ. C2 C2 C2
και(συγκέντρωση/Μ) HCOOΝα(aq) → HCOO-(aq) + Na+(aq)
διίστ./παρ. C1 C1 C1
Υπάρχουν δύο ρυθμιστικά διαλύματα (CH3COOΗ/CH3COO-) και (HCOOΗ/HCOO-), για τα οποία ισχύει: Κα(CH3COOH)=[H3O+]∙[ CH3COO-]/[ CH3COOH] (1) και
Κα(HCOOH)=[H3O+]∙[ HCOO-]/[ HCOOH] (2)Συνέχεια για 1η Εκφώνηση:
Με αντικατάσταση στα(1) και(2) έχουμε:
2∙10-5=[H3O+]∙C2/C1 (3) και 5∙10-4=[H3O+]∙C1/C2 (4)
Οπότε (3)∙(4): 10-8=[H3O+]∙[H3O+]=> 10-4=[H3O+] => pH=4.
H (4) γίνεται: 5∙10-4=10-4 C1/C2 =>5C2=C1 ή 5x=(n-x) =>n=6x
Ποσοστό εξουδετέρωσης CH3COOΗ= (χ/n)∙100%=(1/6)100%=(100/6)%Συνέχεια για 2η Εκφώνηση:( Όταν το ζητούμενο είναι η σταθερά ιοντισμού του HCOOH, είναι άστοχο να ζητηθεί και το pH του διαλύματος ως β, ειδικά αν μοριοδοτήσουμε τα ερωτήματα. Αν θέλουμε να <βοηθήσουμε> πρώτα ζητάμε το pH του διαλύματος και μετά την Κα, διαφορετικά μόνο την Κα.)
Από ποσοστό εξουδετέρωσης του CH3COOΗ έχουμε: (χ/n)∙100%=(1/6)100% => n=6x.
Τότε: C1=(6x-x)/V =5χ/V=5C2.H (1) γίνεται: 2∙10-5=[H3O+]∙C2/5C2 =>[H3O+] =10-4 (Άρα pH=4.)
H (2) γίνεται: Κα(HCOOH)=[H3O+]∙5C2/C2 => Κα(HCOOH)=5∙10-4
-
Προς αποφυγή του %ποσοστού υπό μορφή κλάσματος μπορείτε να δώσετε:
Δίνονται:
Kw = 10⁻¹⁴
Ka(CH3COOH) = 2,5·10⁻⁵
Ka(HCOOH) = 4·10⁻⁴
Η απάντηση είναι 20%. (Τραβηγμένο το Ka(CH3COOH) = 2,5·10⁻⁵ , αλλά και το
Ka(HCOOH) = 5∙10⁻⁴ τραβηγμένο είναι!) -
Παναγιώτη καλημέρα. Και πάλι ωραίος. Νασαι καλά, να γράφεις.
-
Καλημέρα κύριε Παπαστεργιάδη, εξαιρετικη η λύση, ευχαριστουμε πολυ – οι τιμες των σταθερων επιλεγονται για την πιο ευκολη
αλγεβρικη επιλυση, σε μια ‘φορτωμενη’ ουτως ή άλλως ασκηση. Να ειστε καλα -
Καλημερα αγαπητε Δημητρη, ευχαριστω που αντεξες και διαβασες την ασκηση – να εισαι πάντα καλα – περιμενω και το δικο σου πόνημα !
-
Παναγιώτη και πάλι για σου. Πώς θα σου φαινόταν η ακόλουθη πρόταση: Το φορμικό είναι ισχυρότερο οξύ, οπότε θα αντιδράσει πλήρως και θα περισσέψει όλο το οξικό. Άρα, συντελεστής μετατροπής του οξικού 0%.
-
Καλησπέρα σε όλους. Δημήτρη ανάβεις φωτιές! Για να το πεις αυτό πρέπει η Ka των δύο οξέων να διαφέρει σημαντικά, συνήθως 2 τάξεις μεγέθους και πάνω. Αν η ισχύς ειναι παραπλήσια, δεν … Τουλάχιστον αυτό ξέρω εγώ!
-
Καλησπέρα Δημήτρη – ειναι μια προταση που έχει περάσει πιθανώς απο το μυαλο ολων μας – ειδικοτερα αν ειχαμε μαζι ενα ισχυρο κι ενα σθενες οξυ, αν συμφωνεις – νομιζω ομως οτι τα OH- δεν μπορουν να ‘διακρινουν’ την προελευση των H3O+, αρα μαλλον θα εξουδετερωθουν και τα 2 οξεα, με μια μικρη ‘προτιμηση’ οπως φαινεται στο πιο ισχυρο απο τα 2 οξεα.
-
Η σκέψη μου Παναγιώτη βασίζεται σε κάτι άλλο. Αν υποθέσουμε ότι έχουμε ένα διπρωτικό οξύ. Στην ογκομέτρηση δεν περιμένουμε να έχουμε δύο ισοδύναμα σημεία; Κατανάλωση για τη μία μορφή, και μετά για την άλλη. Το γεγονός ότι έχουμε δύο οξέα, από την άποψη της αντίδρασης με τα ιόντα υδροξειλίου, δεν παρουσιάζει κάποια διαφορά. Τι λες;
-
Δημήτρη είδες την απάντηση μου;
-
Αρχικά το ποσοστό εξουδετέρωσης ενός μονοπρωτικού οξέος , όταν μείγμα δύο μονοπρωτικών οξέων αντιδρά με ΝαΟΗ εξαρτάται και από την αναλογία ποσοτήτων μάζας. Στη περίπτωση πού ισχύει: nHA=nHB=nNaOH, περίπτωση που συζητάμε, τότε το ποσοστό εξουδετέρωσης κάθε οξέος εξαρτάται αποκλειστικά από το λόγο των δύο σταθερών ιοντισμού των οξέων. ( Με την υποσημείωση ότι κάθε τελική συγκέντρωση των ΗΑ, ΗΒ, ΝαΑ, ΝαΒ να είναι τουλάχιστον δεκαπλάσια της συγκέντρωσης των οξωνίων.)
Απόδειξη: Από την ενδεικτική απάντηση στην άσκηση που έγινε αφορμή για συζήτηση είχαμε: Κα(ΗΑ)∙ Κα(ΗΒ)=[Η3Ο+]∙[Η3Ο+] ή √Κα(ΗΑ)∙ √Κα(ΗΒ)=[Η3Ο+] και
Κα(ΗΑ)= [Η3Ο+]∙χ/(n-χ) , οπότε √Κα(ΗΑ)/√Κα(ΗΒ)= χ/(n-χ) ή√Κα(ΗΑ)/[√Κα(ΗΒ)+ √Κα(ΗΑ)]= χ/n
Αντίστοιχα αν Κα(ΗΑ)/ Κα(ΗΒ)=Λ2 τότε Λ/(Λ+1) =χ/n
Θοδωρή οι 2 τάξεις μεγέθους δεν είναι αρκετές , γιατί Λ2=0,01 ή Λ=0,1 και ποσοστό εξουδετέρωσης (10/1,1)% του ασθενέστερου οξέος.
Ακόμη και για 4 τάξεις μεγέθους Λ2=0,0001 ή Λ=0,01 και ποσοστό εξουδετέρωσης (1/1,01)% μηδέν δεν γίνεται. -
Καλησπέρα Θωμά. Εντάξει, Θωμά το 1/1,01 είναι σχεδόν 1. Νομίζω υπερβάλεις. Αν η διαφορά στις Κα είναι πάνω από 2 τάξεις μεγέθους, δηλαδή 3 και πάνω, νομίζω είμαστε οκ. Το σφάλμα πρέπει να είναι αμελητέο. Δημήτρη έχεις τίποτα μαζί μου; Γιατί δεν μου μιλάς;
-
Θοδωρή καλησπέρα. Εσύ το νοιώθεις υπερβολή, εγώ το εννοώ επιστημονική εγκυρότητα. Οι προσεγγίσεις που γίνονται ΔΕΝ πρέπει ΠΟΤΕ να οδηγούν σε επιστημονικά σφάλματα! Αν ένα υδατικό διάλυμα ασθενούς οξέος ΗΑ στους 25 oC , έχει pΗ =6,9 δεν θα πεις ΠΟΤΕ , ότι έχει pΗ =7. Αυτό θα σήμαινε ότι το οξύ ΔΕΝ ιοντίζεται, δηλαδή α=0 , ενώ ο α τείνει στη μονάδα! Ανάλογα είναι και εδώ. Το 0% ποσοστό εξουδετέρωσης, σημαίνει ότι το ασθενές οξύ ΔΕΝ αντιδρά με την βάση, που είναι ΛΑΘΟΣ!!
Στο άλλο με το άθροισμα των ποσοστών έχεις δίκιο να γράφεις ότι το άθροισμά τους δεν κάνει 100%. ΔΕΝ χρειάζονται ιδιαίτερες πράξεις. Αν από 0,05mol HA και 0,05mol HΒ εξουδετερώνονται χ mol HA και (0,07-χ) mol HΒ από 0,07mol ΝαΟΗ, τότε [χ/0,05 +(0,07-χ)/0,05]∙100%=140%. Τότε όμως, δηλαδή με 0,07mol ΝαΟΗ, και ίδια τα υπόλοιπα για να βρεις το pΗ πρέπει να ξέρεις το ποσοστό εξουδετέρωσης του ενός ή για να βρεις το ποσοστό εξουδετέρωσης του ενός πρέπει να ξέρεις το pΗ. ( Μου θύμησες συζητήσεις που έκανα το Σεπτέμβρη του 2020.) -
Θοδωρή καλησπέρα. Μόλις τώρα έχω πάλι επαφή με υπολογιστή και διάβασα τα σχόλια. Εξακολουθώ να έχω την ίδια απορία. Όταν αντιμετωπίζουμε μια ογκομέτρηση διπρωτικού οξέος, με δύο ισοδύναμα σημεία, ολοκληρώνεται ο ένας ιοντισμός και μετά παίρνουμε τον δεύτερο (γι’ αυτό και δύο ΙΔ, συνοπτικά φυσικά αυτό που γράφω). Η επίλυση της άσκησης του Παναγιώτη δεν χρησιμοποιεί τη διαφορά των Κα. Οπότε το ερώτημα είναι γιατί η διαφορετική προσέγγιση στα δύο προβλήματα;
Τώρα όσον αφορά στη διαφορά των Κα Θοδωρή σου στέλνω μια παραπομπή και να μου πεις τη γνώμη σου. (Simultaneous determination of mixtures of acids by potentiometric titration, https://doi.org/10.1016/S0003-2670(98)00185-8) -
…..η γνώμη μου είναι επίσης ότι η βασική ιδέα της ανάρτησης για τους μαθητές είναι να χειρίζονται τα εν λόγω δεδομένα για εξοικείωση κυρίως και λιγότερο να μπορούν να αιτιολογήσουν την διαφορά στα πολυπρωτικα οξέα και στα μείγματα οξέων
-
Καλησπέρα , ίσως να παίζει ρόλο και το ακόλουθο: Στα πολυπρωτικά οξέα υπάρχει μεγάλη διαφορρά μεταξύ των διαδοχικών Ka (Ka1 >> Ka2 >> Ka3). Κάθε αποπρωτονίωση αυξάνει το αρνητικό φορτίο της χημικής οντότητας, οπότε η επόμενη γίνεται πολύ δυσκολότερα. Γι’ αυτό η εξουδετέρωση γίνεται διαδοχικά και εμφανίζονται ξεχωριστά στάδια.
Σε ένα μείγμα δύο διαφορετικών οξέων, όπως εδώ οι τιμές Ka είναι συνήθως πιο κοντινές και τα οξέα είναι ανεξάρτητα μεταξύ τους. Έτσι συμβάλλουν ταυτόχρονα στο pH και η βάση κατανέμεται μεταξύ τους, οδηγώντας σε παράλληλη μερική εξουδετέρωση.
-
Παναγιώτη ευχαριστώ για την απάντηση. Όσον αφορά την αξία της άσκησής σου, έχεις δίκιο για τους μαθητές και τον στόχο σου.
Πάντως σκέφτομαι να λύσω την άσκηση ως εξής, μόλις βρω χρόνο. Να αντιδράσει η βάση με το ένα οξύ (ισότητα mol) και μετά να προσθέσω το 2ο οξύ και να υπολογίσω ποσοστό μετατροπής και pH. Ίσως έχει ενδιαφέρον. -
Καλησπέρα. Παναγιώτη συμφωνώ αλλά θα κάνω ακόμα ένα σχόλιο. Θωμά σε διάλυμα ασθενούς μονοπρωτικού οξέος κάνουμε προσέγγιση όταν α <= 0,1. Κάνουμε δηλαδή δεκτό σφάλμα μέχρι και 10%. Όταν κάνουμε προσεγγίσεις δεν κάνουμε “εκπτώσεις” στην επιστημονική εγκυρότητα. Οι προσεγγίσεις γίνονται ώστε, όταν δεν απαιτείται πολύ μεγάλη ακρίβεια, να απλοποιήσουμε τους υπολογισμούς.
Δημήτρη και Θωμά μεταφέρω και κάτι από το έγκυρο βιβλίο “Σύγχρονες Μέθοδοι στη Χημική Ανάλυση” των Pecsok-Shields-Cairns-McWilliam, απόδοση στα ελληνικά Σταύρος Βολιώτης, Εκδόσεις Πνευματικός : σελ. 510 “Αν οι διαδοχικές pK ενός διπρωτικού οξέος διαφέρουν κατά 3 ή περισσότερο, η καμπύλη τιτλοδότησης αποτελείται από δύο μονοπρωτικές καμπύλες. Καθώς οι τιμές pK πλησιάζουν η μία την άλλη, οι δύο καμπύλες συγχονεύονται σε μια απλή, και το ισοδύναμο σημείο του πρώτου πρωτονίου εξαφανίζεται” (έχει και τα σχετικά σχήματα). Και παρακάτω: Για να πετύχουμε ένα ικανοποιητικό τέλος τιτλοδότησης σε ένα σύστημα πολυπρωτικού οξέος, δύο τουλάχιστον διαδοχικές τιμες pK πρέπει να διαφέρουν το λιγότερο κατά 3, και το τέλος της τιτλοδότησης να γίνεται σε pH από 4 έως 10″. Νομίζω αυτά δικαιολογούν αυτά που έχω ισχυριστεί έως τώρα. -
Δημήτρη εγώ σε ευχαριστώ για τον χρόνο σου και τις ιδέες σου , τσεκαρε αυτό που λες , έχει ενδιαφέρον
-
Θοδωρή καλησπέρα.
Μάλλον με παρεξήγησες. Δεν αμφισβητώ τίποτα από αυτά που αναφέρεις. Ολόσωστα. Απλά ανέφερα το άρθρο (έπεσα πάνω του πριν από 10 ημέρες) γιατί μου έκανε εντύπωση. Προσδιορίζει ποσοτικά μίγμα οξέων, με ποτενσιομετρία, ανεξάρτητα από ka.
Έτσι κι αλλιώς, το όλο θέμα ξεκίνησε από την ερώτηση που είχα θέσει, που όμως είναι λάθος γιατί παραλείπει την επίδραση που θα έχει στο pH η προσθήκη του επόμενου οξέος.
Καλό βράδυ. -
Kαλημέρα σε όλους. Θα ήθελα να ρωτήσω πως θα υπολογίζατε το pH ενός διαλύματος στο οποίο προσθέτουμε 0,1mol CH3COOH, 0,1mol CH3COONa, 0,2mol HCOOH και 0,2mol HCOONa με τελικό όγκο 1L.
-
Καλημέρα Άγγελε (πολύ καλή ερώτηση) και στους υπολοιπους
Με Gemini ιδέες και λιγο βιαστικα
Kw = 10⁻¹⁴
Ka(CH3COOH) = 2·10⁻⁵
Ka(HCOOH) = 5·10⁻⁴
Πως θα υπολογίζατε το pH ενός διαλύματος στο οποίο προσθέτουμε 0,1mol CH3COOH, 0,1mol CH3COONa, 0,2mol HCOOH και 0,2mol HCOONa με τελικό όγκο 1L.
pH=3,3 αν γινουν οι πραξεις με το HCOOH
pH=4,7 αν γινουν οι πραξεις με το CH3COOHΓιατί δεν χρησιμοποιούμε το οξικό σύστημα;Αν δοκιμάσετε να υπολογίσετε το pH χρησιμοποιώντας το οξικό σύστημα με τις αρχικές του συγκεντρώσεις, θα βρήκατε pH = 4,7. Ωστόσο, επειδή το μυρμηκικό σύστημα απελευθερώνει περισσότερα H3O+, η ισορροπία του οξικού μετατοπίζεται προς τα αριστερά (σύμφωνα με την αρχή Le Chatelier), καταναλώνοντας οξικά ιόντα και παράγοντας αδιάστατο οξικό οξύ, μέχρι η σχέση [CH3COO-]/[CH3COOH] να προσαρμοστεί στο pH = 3,3 που επέβαλε το ισχυρότερο οξύ.
εαν θεωρησουμε
Kw = 10⁻¹⁴
Ka(CH3COOH) = 10⁻⁵
Ka(HCOOH) = 10⁻⁴έχουμε αντιστοιχα
pH=4 αν γινουν οι πραξεις με το HCOOH
pH=5 αν γινουν οι πραξεις με το CH3COOHΠροφανως μαλλον οχι καταλληλο θεμα για παιδιά
Αντιγραφω μια ασκηση του Θοδωρη Βαχλιωτη (είδες που φύλαξα το pdf;) με πιο ΄κατάλληλη διατυπωση’
Υδατικό διάλυμα Δ περιέχει τα ασθενή μονοπρωτικά οξέα ΗΑ 0,1 Μ και ΗΒ 0,5 Μ και τα άλατά τους NaA 0,2 Μ και NaB 0,1 Μ.
α. Να υπολογίσετε το pH του διαλύματος Δ. [pH=4]
β. Να συγκρίνετε την ισχύ των οξέων ΗΑ και ΗΒ. [HA>HB]
Δίνεται για το οξύ ΗΑ: Ka=2.10-4.Καλημέρα σε όλους
-
Καλησπέρα. Σε αυτήν την περίπτωση Άγγελε γίνεται η αντίδραση
HCOOH + CH3COO- <=> HCOO- + CH3COOH
με Κc = Ka(HCOOH) / Ka(CH3COOH) = 5*10^-4 / 2*10^-5 = 25.
Αν υπολογίσεις το Qc = 1 < Κc και γίνεται αντίδραση προς τα δεξιά.
Ξεφύγαμε!
-
Καλησπερα σε ολους
Δημητρη πολυ καλη η ιδεα σου.
Η τιμη του pH του διαλυματος που θα προτεινα θα ηταν 4 (όχι 4 ή 5) αν περναμε υποψη μας το γεγονος οτι το pH το καθοριζει το
ισχυρο οξυ κυριως, για τα ακολουθα δεδεομεναKw = 10⁻¹⁴
Ka(CH3COOH) = 10⁻⁵
Ka(HCOOH) = 10⁻⁴
pH ενός διαλύματος στο οποίο προσθέτουμε 0,1mol CH3COOH, 0,1mol CH3COONa, 0,2mol HCOOH και 0,2mol HCOONa με τελικό όγκο 1L.Ωστόσο μάλλον ο πιο γενικόw τροπος ειναι η επιλυση μεσω της μέθοδου του ισοζυγίου φορτίου
[H3O+] + [Na+] = [OH-] + [HCOO-] + [CH3COO-]
για τα ακολουθα δεδεομεναKw = 10⁻¹⁴
Ka(CH3COOH) = 10⁻⁵
Ka(HCOOH) = 10⁻⁴
pH ενός διαλύματος στο οποίο προσθέτουμε 0,1mol CH3COOH, 0,1mol CH3COONa, 0,2mol HCOOH και 0,2mol HCOONa με τελικό όγκο 1L.Είναι ο πιο αυστηρός επιστημονικά τρόπος για να λυθεί οποιοδήποτε πρόβλημα ιοντικής ισορροπίας, (δεν βασίζεται σε παραδοχές).
Το αποτέλεσμα που προκυπτει απο GEMINI ειναι pH=4,3
Αν παρατηρηστε ειναι κοντα στην τιμη 4 αν περναμε υποψη μας το γεγονος οτι το pH το καθοριζει το
ισχυρο οξυ κυρίως, η συνεισφορα του +0,3 οφειλεται και στην υπαρξη του CH3COOH. -
ισως εχει να κανει και με την παρουσια του CH3COONa, εχω ενσωματωσει και την απαντηση απο το gemini στα google docs
-
Καλησπέρα. Παναγιώτη μήπως το pH βγαίνει περίπου 3,7; Τόσο το υπολόγισα. Η συνεισφορά του αιθανικού πρέπει να ελαττώνει το pH κατά 0,3.
Και στο chatgtp 3,7 το βγάζει. -
ΠΡΟΒΛΗΜΑ ΙΣΟΡΡΟΠΙΑΣ ΜΕΙΓΜΑΤΟΣ ΡΥΘΜΙΣΤΙΚΩΝ ΔΙΑΛΥΜΑΤΩΝ
1. ΔΕΔΟΜΕΝΑ
· CH3COOH (Οξικό οξύ): 0,1 mol (Αρχικά)
· CH3COONa (Οξικό νάτριο): 0,1 mol (Αρχικά)
· HCOOH (Μυρμηγκικό οξύ): 0,2 mol (Αρχικά)
· HCOONa (Μυρμηγκικό νάτριο): 0,2 mol (Αρχικά)
· Τελικός όγκος: 1 L
· Ka(CH3COOH) = 10^-5 (pKa = 5)
· Ka(HCOOH) = 10^-4 (pKa = 4)
2. ΜΕΘΟΔΟΣ ΙΣΟΖΥΓΙΟΥ ΦΟΡΤΙΟΥ (Charge Balance)
Η θεμελιώδης εξίσωση για το διάλυμα είναι:
[H3O+] + [Na+] = [OH-] + [CH3COO-] + [HCOO-]
Γνωρίζουμε ότι:
· [Na+] = 0,3 M (0,1 από το οξικό + 0,2 από το μυρμηγκικό νάτριο)
· [CH3COO-] = C(ολικό1) * Ka1 / (Ka1 + [H3O+])
· [HCOO-] = C(ολικό2) * Ka2 / (Ka2 + [H3O+])
3. ΜΑΘΗΜΑΤΙΚΗ ΕΠΙΛΥΣΗ
Αντικαθιστώντας τις τιμές στην εξίσωση φορτίου (θέτοντας x = [H3O+]):
x + 0,3 = (0,2 * 10^-5) / (10^-5 + x) + (0,4 * 10^-4) / (10^-4 + x)
Με την παραδοχή x << 0,3 και λύνοντας τη δευτεροβάθμια εξίσωση που προκύπτει:
x^2 – (3 * 10^-5)x – 10^-9 = 0
Η διακρίνουσα είναι Δ = 49 * 10^-10.
Η θετική ρίζα της εξίσωσης είναι:
x = 5 * 10^-5 M
4. ΤΕΛΙΚΟ ΑΠΟΤΕΛΕΣΜΑ
[H3O+] = 5 * 10^-5 M
pH = -log(5 * 10^-5) = 5 – log5 = 5 – 0,7
pH = 4,3
5. ΕΠΑΛΗΘΕΥΣΗ ΠΟΣΟΤΗΤΩΝ (Ανά 1 Λίτρο)
Λόγω της διαφοράς ισχύος των οξέων, έγινε η αντίδραση:
HCOOH + CH3COO- <-> HCOO- + CH3COOH
Κατά την οποία αντέδρασαν περίπου 0,067 mol.
Τελικές συγκεντρώσεις ισορροπίας:
· [CH3COOH] = 0,167 M
· [CH3COO-] = 0,033 M
· [HCOOH] = 0,133 M
· [HCOO-] = 0,267 M
Επαλήθευση μέσω Henderson-Hasselbalch:
pH = 5 + log(0,033/0,167) = 4,3
pH = 4 + log(0,267/0,133) = 4,3 -
Παναγιώτη καλημέρα. Αναρτώ την απάντηση που σου ανέφερα. Ίσως έχει κάποιο ενδιαφέρον. Για την απάντησή σου στον Άγγελο, δεν κατάλαβα κάτι. Όταν υπολογίζεις το pH με το HCOOH παίρνεις μία τιμή και με το CH3COOH παίρνεις άλλη; Αν λες αυτό δεν μπορεί να είναι σωστό. Το pH έχει μία τιμή. Μήπως κάτι δεν κατάλαβα;
https://i.ibb.co/Rknk0qHJ/23d.jpg -
Με πιο ακριβείς τιμές Ka βγαίνει πιο κάτω. Το chatgtp με Κα=10-4 και 10-5 το βγάζει 3,8 το pH.
-
Τώρα μου το βγάζει 4,15 το chatgtp. Μάλλον εσύ έχεις δίκιο Παναγιώτη
-
Άγγελε καλησπέρα. Και εγώ pH 3,7 βρήκα λύνοντας τη δευτεροβάθμια. Αλλά το chatgtp δίνει άλλο αποτέλεσμα. Δεν ξέρω ποια είναι η ακριβής τιμή.
-
Θα ήταν καλό αν μπορούσαμε να το ελέγξουμε πειραματικά. Στα σχολικά εργαστήρια βέβαια δεν διαθέτουμε τα αντιδραστήρια αλλά και τα πεχάμετρα δεν είναι πλέον βαθμονομημένα.
-
Παναγιώτη καλημέρα. Μία ερώτηση. Στη λύση που παραθέτεις γράφεις: [CH3COO-] = C(ολικό1) * Ka1 / (Ka1 + [H3O+]). Πώς προκύπτει αυτό και τι είναι το C(ολικό1). Ευχαριστώ.
-
Δημητρη, απο gemini:
Στην άσκησή μας, βάλαμε 0,1 mol CH3COOH και 0,1 mol CH3COONa. Άρα: C(ολικό1) = 0,1 + 0,1 = 0,2 M.
Ξεκινάμε από τη σταθερά ιοντισμού (Ka): Ka = [H3O+] * [CH3COO-] / [CH3COOH] (Σχέση 1)
Και από το ισοζύγιο μάζας (αυτό που είπαμε παραπάνω): C(ολικό) = [CH3COOH] + [CH3COO-] (Σχέση 2)
Από τη Σχέση 2, λύνουμε ως προς το αδιάστατο οξύ: [CH3COOH] = C(ολικό) – [CH3COO-]
Αντικαθιστούμε αυτό στη Σχέση 1 (της Ka): Ka = [H3O+] * [CH3COO-] / (C(ολικό) – [CH3COO-])
Κάνουμε χιαστί: Ka * (C(ολικό) – [CH3COO-]) = [H3O+] * [CH3COO-] Ka * C(ολικό) – Ka * [CH3COO-] = [H3O+] * [CH3COO-]
Μεταφέρουμε το [CH3COO-] στο ίδιο μέλος: Ka * C(ολικό) = [H3O+] * [CH3COO-] + Ka * [CH3COO-]
Βγάζουμε κοινό παράγοντα το [CH3COO-]: Ka * C(ολικό) = [CH3COO-] * ([H3O+] + Ka)
Λύνουμε ως προς [CH3COO-] και έχουμε τον τύπο μας: [CH3COO-] = C(ολικό) * Ka / (Ka + [H3O+])
-
Τα είχαμε πεί κάποτε Θοδωρή …
https://i.ibb.co/fZg22qF/2427c064-3bf4-4ee4-a5f4-9cf034230fe2-1771149658-2037.jpg
-
Θοδωρή κι εγώ βγάζω 4,15. Επισυνάπτω τη λύση μου. Άλλαξα τους συβολισμούς των οξέων για συντομία.
-
Συγνώμη που καθυστέρησα λόγω υποχρεώσεων να απαντήσω. Θοδωρή κι εγώ όταν υπέβαλα το ερώτημα στο forum, είχα προσεγγίσει το θέμα σαν ισορροπία των 4 ειδών, αλλά το είχα συνεχίσει εκεί που είπες ότι ξεφύγαμε με επίλυση δευτεροβάθμιας, αλλά την είχα πάρει ανάποδα με Kc=0,04, βρήκα ότι θα πάει αριστερά κατά 0,082mol και κατέληξα σε pH=3,7. Στο ίδιο αποτέλεσμα καταλήγει και το pHsolver του webqc.org η οποία είναι η μόνη μηχανή υπολογισμού pH που βρήκα (από όσες έψαξα) που δέχεται πολλά συστατικά στο διάλυμα.
https://i.ibb.co/qF3sJTnm/Screenshot-2026-02-14-220440-1771099919-4707.png
-
Καλησπέρα. Αντώνη δεν έχεις βάλει λάθος τη συγκέντρωση του HCOOH στην Ka; Είναι 0,1175 όχι 0,0175. Αν βάλεις 0,1175 βγαίνει pH 3,7.
ΥΓ: Πολλά είχαμε πει κάποτε, αλλά μπορούμε να πούμε κι άλλα … Αν θες …
-
Νομίζω αυτό έχω βάλει … να σου πω την αληθεια “ούτε που με νοιάζει”. Η άσκηση λύνεται ως ΧΙ κτλ και καταλήγουμε σε “εκεινο” το θέμα των πανελληνίων ( επί δεσμών ) που είχε τις ουσίες ( ή εννοούσε ότι είχε ) σε ισορροπία.
Το μόνο ενδιαφέρων που θα συζητούσα θα ήταν η ποιοτική μελέτη της σύγκρισης της τιμής της Qc ( 1 ) με την Kc ( 25 ). Μοιάζει αυτή η διαφορά να μην είναι αρκετή για να θεωρήσουμε μια ισορροπία ώς μονόδρομη ( μεταφέροντας το 10 % της αποδεκτής προσέγγισης της ισοντικής στη “μοριακή” ισορροπία ).
Θα το ψάξω ( λέμε τώρα ).
Για αρχή πρέπει να βρούμε την ανάρτηση που είχε αναδείξει το θέμα πριν από ( 100 ? ) χρόνια. Νομίζω συντάκτης ήταν ο Ελευθερίου ( ή ο Πολυνίκης ) με τίτλο “ανάμειξη ρυθμιστικων δ/των ).
Θα δώσω 5 min στην αναζήτηση … ( αλλά βαριέμαι :-).
-
Την βρήκα … 2010 !!! …. 15 χρόνια πριν …
Ακόμα ανακαλύπταμε τη χημεία ( Τι βλακείες γράφαμε ).
-
Μια συνάδελφος φιλόλογος, πιο έμπειρη από εμένα τότε, μου είχε πει πριν από χρόνια: “Αγοράκι μου, αν δεν βγάλεις ρυτίδες μερικά πράγματα δεν…” Αυτό που με ανησυχεί είναι ότι, ακόμα, δεν έχω βγάλει ρυτίδες! Χαχα
-
-
H/o Παναγιώτης Κουτσομπόγερας έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 1 μέρα
Πορφυρογέννητοι βασιλιάδες, ταπεινά κοχύλια και Br
 Το Βυζάντιο συνδέθηκε όσο λίγοι πολιτισμοί με το χρώμα και τον συμβολισμό του. Η περίφημη πορφύρα ήταν κάτι πολύ περισσότερο από βαφή: αποτελούσε […]
Το Βυζάντιο συνδέθηκε όσο λίγοι πολιτισμοί με το χρώμα και τον συμβολισμό του. Η περίφημη πορφύρα ήταν κάτι πολύ περισσότερο από βαφή: αποτελούσε […]-
Καλησπέρα Παναγιώτη. Πολύ ενδιαφέρουσες πληροφορίες. Το Br στον τίτλο που κολλάει; Στο βρώμιο αναφέρεσαι;
-
α, σόρι, τωρα κατάλαβα, υπάρχει βρώμιο στο μόριο της πορφύρας
-
Καλησπέρα αγαπητέ Πορφυρογέννητε Θοδωρή !
-
Γεια σου Παναγιώτη. Για το Tyrian Purple ένα άρθρο, που κατά σύμπτωση διάβασα χθες. Λέγεται ότι για να παραχθεί ένα γραμμάριο βαφής, έπρεπε να χρησιμοποιηθούν περίπου 12000 πορφύρες!
-
Καλησπέρα Αποστολε Παλαιολογε! Πολύ χρήσιμη η πληροφορία σου , δεν ήξερα την τόσο μεγάλη αξία της χρωστικής. Σ’ ευχαριστώ πολυ
……. Μήπως να κάνεις ένα τομέα για οικονομικά μαθηματα κατεύθυνσης στο Υλικονετ ; Καλό απόγευμα -
Παναγιώτη, είμαι ο τελευταίος που θα μπορούσε να κάνει κάτι τέτοιο. Ομολογώ ότι δεν σκαμπάζω τίποτε από οικονομικά, εκτός από αυτό: τα όμορφα πράγματα στη ζωή μας δεν αποτιμώνται με οικονομικούς όρους.
-
Αποστόλη τα είπες όλα με το ‘….τα όμορφα πράγματα στη ζωή μας δεν αποτιμώνται με οικονομικούς όρους.’
-
- Φόρτωσε Περισσότερα
Γειά σου Γιάννη. Παρέμεινε ίδια. Δεν ανταλλάσσει το αέριο ενέργεια με το περιβάλλον ούτε με το μηχανισμό του έργου ούτε με το μηχανισμό της θερμότητας . Συνεπώς η εσωτερική ενέργεια του παραμένει σταθερή (1ος θερμοδυναμικός Νομός), άρα και η θερμοκρασία του (U=3/2nRT). Ας τρέχει το αεροπλάνο όσο γρήγορα θέλει. Αρκεί να είναι σταθερή η ταχύτητα του (αδρανειακό σύστημα).
Καλησπέρα Γιάννη.
Η θερμοκρασία του αερίου συνδέεται με τη μέση μεταφορική κινητική ενέργεια των μορίων του εξαιτίας της άτακτης κίνησής τους. Της κίνησης που ονομάζουμε θερμική. Συνδέεται δηλαδή με την εσωτερική ενέργεια του αερίου.
Η κινητική ενέργεια λόγω κίνησης του δοχείου (ταχύτητα του αεροπλάνου) δεν είναι άτακτη κίνηση, αλλά οργανωμένη. Είναι μια μηχανική ενέργεια και όχι εσωτερική ενέργεια. Δεν συνδέεται με θερμοκρασία.
Καλησπέρα Γιώργο και Διονύση.
Ευχαριστώ για τη συμμετοχή και τα σχόλια.
Αν ήξερα την απάντηση δεν θα άνοιγα ίσως το θέμα.
Αλλά ο Γιαννακόπουλος με την περιστροφή του δοχείου και ο Μάλινχωφ με εκείνη την υπέροχη προσομοίωση!!.
Είπα λοιπόν να παραστήσω το Μάλινχωφ:
https://i.ibb.co/fdgTmZYQ/1.png
Βλέπουμε ένα δοχείο που τρέχει με 10 m/s και τα μόρια μέσα επίσης με 10m/s.
Ακίνητα ως προς το δοχείο.
Το αέριο έχει θερμοκρασία 0 Κ.
Το δοχείο φρενάρει. Λίγη ώρα μετά την ακινητοποίηση:
https://i.ibb.co/BVx8j4tP/22.png
Τα μόρια δεν είναι ακίνητα ως προς το δοχείο. Το αέριο δεν είναι στο απόλυτο μηδέν!!
Ο φοβερός Μάλινχωφ μας το είχε ξαναδείξει. Οργανωμένη κινητική ενέργεια μετατρέπεται σε ανοργάνωτη σε καθεστώς πλήρως ελαστικών κρούσεων σε εκείνη την εκπληκτική προσομοίωση.
Διονύση δεν υπάρχει πλαστική κρούση εδώ.
Η προσομοίωση:
Ξεκινάει με 300 οργανωμένη, δηλαδή μηδέν εσωτερική ενέργεια.
Καταλήγει με 600 ανοργάνωτη!!
Δεν είπα Γιάννη ότι είναι πλαστική κρούση!
Είπα ότι και σε μια πλαστική κρούση, όλη η κινητική ενέργεια μετατρέπεται σε θερμική αυξάνοντας την εσωτερική ενέργεια άρα και τη θερμοκρασία του σώματος…
Όπως βλέπεις στην προσομοίωση το δοχείο φρενάρει χωρίς πλαστικότητες σε τοίχο.
Το έβαλα να κάνει επιβραδυνόμενη κίνηση με α=-2m/s^2.
Τη μεταβολή της ενέργειας τη βλέπουμε καθαρά.
Δεν ξέρω ακόμα τι συμβαίνει με την περίπτωση της ερώτησης.
Όμως η προσομοίωση είναι εύγλωττη.
Να το πω με άλλα λόγια.
Και στην πλαστική κρούση έχουμε υποβάθμιση της ενέργειας, όπως και στο παράδειγμά σου με την προσομοίωση.
Γιάννη ένα σώμα κινείται με ταχύτητα υ και συγκρούεται με ένα τοίχο, όπου κολλάει (πλαστική κρούση).
Η οργανωμένη μηχανική ενέργεια (κινητική) του σώματος 1/2mυ^2 μετατρέπεται σε θερμική. Δεν είναι το ίδιο με την εικόνα που παρουσιάζεις;
Βέβαια το κονκόρντ δεν θα κτυπήσει σε τοίχο να ακινητοποιηθεί…
Γιάννη μάλλον το ; χάλασε το νόημα…
Ήθελα να γράψω: “Δεν είναι το ίδιο με την εικόνα που παρουσιάζεις;” και
έγραψα: “Δεν είναι το ίδιο με την εικόνα που παρουσιάζεις.”
Ναι έγραψες το σχόλιο όσο σουλούπωνα την προσομοίωση και δεν το είδα.
Εδώ βλέπουμε επίσης μετατροπή οργανωμένης σε ανοργάνωτη.
Να πούμε ότι το αέριο θερμαίνεται;
Πιθανόν…
Γιάννη οι νόμοι της φυσικής έχουν τη μορφή που γνωρίζουμε μόνο σε αδρανειακά συστήματα αναφοράς. Αυτό ισχύει για το πρώτο θερμοδυναμικό Νόμο και για τα συμπεράσματα της κινητικής θεωρίας. Για αυτό αναφέρθηκαν στο προηγούμενο σχόλιο μου σε αδρανειακό σύστημα. Βέβαια για μικρές επιταχύνσεις όπως αυτές ενός αεροπλάνου που μεταφέρει ανθρώπους πιθανώς να είναι αμελητέες οι τροποποιήσεις που προκαλούνται σε αυτούς τους νόμους. Όπως δεν λαμβάνουμε υπόψη τη βαρύτητα (g=10m/s^2- αρχή της ισοδυναμίας). Συνεπώς η απάντηση μου είναι η ίδια. Απάντησα βάσει του θέματος που θέτεις στην αρχική του διατύπωση.
Σωστα Γιάννη διοτι ενας παρατηρητης που κινειται μαζι με το δοχειο και βλεπει ολα τα μορια ακινητα,δηλαδη με εσωτερικη ενεργεια μηδεν,οταν αυτο αρχισει να επιταχυνεται,βλεπει να εμφανιζεται ενα πεδιο βαρυτητας το οποιο δρα πανω στα σωματιδια του αεριου και να τους δινει κινητικη ενεργεια δαπαναις της δυναμικης τους.Αρα η επιταχυνση οτι φορά και να εχει θα αυξησει τηνθερμοκρασια.
Καλησπέρα Γιάννη. Στην εκφωνηση γράφεις θερμοκρασία 273Κ. Στην συζήτηση που ακολουθεί όμως παίρνεις θερμοκρασία 0 Κ!
Γιώργο μια συμπλήρωση:
Οι νόμοι της Φυσικής ισχύουν και σε μη αδρανειακά συστήματα και έχουν την ίδια μορφή.
Πρέπει βέβαια να βάλουμε στο παιγνίδι της αδρανειακές δυνάμεις,
Μια επιβράδυνση του αεροσκάφους γεννά δυνάμεις D’ Alenbert και κάτι σαν πρόσθετο βαρυτικό πεδίο. Μεταβολή της συγκέντρωσης των μορίων του αερίου.
Όταν σταματήσει το αεροσκάφος εξαφανίζεται αυτό το βαρυτικό πεδίο και έχουμε μια ανακατανομή. Θα προκαλέσει θέρμανση;
Δεν το ξέρω.
Σίγουρα δεν μιλάμε για θερμάνσεις μεγάλες. Δεν γίνεται καυτό το αέριο.
Στο πρώτο σου σχόλιο λες:
Αρκεί να είναι σταθερή η ταχύτητα του (αδρανειακό σύστημα).
Δεν είναι. Τρέχει με 700 m/s στη μέση της διαδρομής και σταματάει λίγο πριν την αποβίβαση.
Κωνσταντίνε αυτό σκέφτομαι αλλά δεν έχω απάντηση.
Ούτε μπορώ να κάνω υπολογισμό με τα δεδομένα που έδωσα.
Ναι Γιώργο 0 Κ για να φανεί στην προσομοίωση χωρίς κανένα υπολογισμό η αύξηση.
Ότι συμβαίνει στους 0 Κ συμβαίνει και στους 273 Κ ;
Δεν ξέρω.
Γιάννη γιατί λες ότι δεν ξέρεις;
Η διατήρηση της ενέργειας δεν μας λέει ότι η κινητική ενέργεια του αερίου ίση με την κινητική ενέργεια του κέντρου μάζας, άρα ½ mυ^2, όπου m=4g και υ=υcm=700m/s, θα μηδενιστεί; Αλλά τότε θα έχουμε ίση αύξηση της εσωτερικής ενέργειας, άρα:
https://i.ibb.co/Pv1nCbqs/2026-02-19-194824.png
Δεν είναι έτσι;
Διονύση ας δούμε αυτό που είπες πιο αναλυτικά:
https://i.ibb.co/r2djSvyL/45.png
Όμως 104 βαθμοί είναι εξωφρενική διαφορά.
Τέτοιες διαφορές θα προκαλούσαν ανάφλεξη του αεροπλάνου.
Διατηρείται η ενέργεια του αερίου ή μειώνεται διότι δέχεται δυνάμεις από τα τοιχώματα που δεν είναι ίσες κατά τη διεύθυνση της κίνησης;
Η ώθηση της δύναμης D’ Alembert θα έδινε απάντηση;
Μήπως η όποια αύξηση σχετίζεται με το έργο των δυνάμεων D’ Alembert που προκαλούν μια μετατόπιση μικρή του κέντρου μάζας του αερίου;
Ο Γιαννακόπουλος μιλάει για μία έλικα που στρεφόμενη θερμαίνει το αέριο.
Ένα ταρακούνημα του δοχείου δεν έχει ανάλογο αποτέλεσμα;
Καλησπέρα Γιάννη και Διονύση. Είχα γράψει το εξής.Όταν το δοχείο κινείται μαζί με το concord τα μόρια του αερίου έχουν μεταφορική κινητική ενέργεια πέραν από αυτή εξαιτίας της άτακτης κίνησής τους. Όταν σταματήσει το αεροπλάνο η ενέργεια αυτή δεν μπορεί να δοθεί στο περιβάλλον λόγω της ποιότητας των τοιχωμάτων (αδιαβατικά και ακλόνητα). Αφού η ΚΥΥΡΙΑ, που έλεγε ο Αντρέας, δεν χάνεται θεωρώ ότι θα κατανεμηθεί στα ίδια τα μόρια μέσω των μεταξύ των κρούσεων Άρα μπορώ να πω. https://i.ibb.co/fdkGzX4t/Capture.jpgΠου δίνει ΔΤ≈78.6 Κ
Γεια σου Άρη.
Πολύ δεν είναι;
Ίσως Γιάννη φταίει η μεγάλη ταχύτητα του cocord, Αλλά σκεφτόμενος ενεργγειακά δεν μπορώ να δώ κάτι άλλο. Που να πάει η κινητική ενέργεια λόγω μεταφοράς.
Δεν ξέρω Άρη.
Μήπως μόνο αντιστέκεται στην επιβράδυνση;
Ήταν η τζάμπα εκδοχή του chatgpt.
Ερώτηση: Με την ίδια λογική και ο αερας που βρίσκεται μέσα σε εμας που είμαστε στο αεροπλάνο δεν θα αυξηθεί η θερμοκρασία του τόσο πολύ και θα μεταφερθεί στο σώμα μας;
Βεβαίως Γιώργο.
Μάλιστα με αύξηση 70 βαθμών στην καλύτερη περίπτωση θα το πάρουμε χαμπάρι, στη χειρότερη θα αποδημήσουμε εις Κύριον.
Έτσι μάλλον πρόκειται για πολύ μικρή αύξηση που (ίσως) οφείλεται στην ανάδευση λόγω D’ Alembert ή αν προτιμάμε λόγω επιβράδυνσης.
Πάρε ένα μπαλόνι και ταρακούνησέ το. Πόσο θα ζεσταθεί;
Θα το πάρουμε είδηση;
Αυτό είδα (μετα τις αναγκαίες πραξεις) και για αυτό αναρωτιέμαι. και κάνω τις ερωτήσεις. Κατι άλλο θα συμβαίνει. Θα το σκεφτω αργότερα .
Γιάννη χωρίς να μπορώ να βρω κάτι ουσιαστικά διαφορετικό έπαιξα με την ταχύτητα.Μέγιστη πραγματική ταχύτητα των concord ήταν 2180km/h ή 605m/sΤότε βγαίνει ΔΤ= 58.7 Κ πάλι μεγάλο θα πεις.Όμως δεν πάει από 2180km/h στα 0 km/h.Αν λοιπόν πούμε ότι προσγειώνεται με 100 km/h τότε βγαίνει ΔΤ= 1,59 Κ !!!!Υποθέτω γεν έκανα πατάτα στις πράξεις.
Άρη διατηρείται η ενέργεια;
Συνάδελφοι Καλησπέρα
Δεν ξέρω αν κάνω Λάθος , αλλά έχω την αίσθηση ότι στριφογυρίζουμε γύρω από τα ίδια θέματα . Θέματα που φέρνουν στα όριά τους μοντέλα όπως το μοντέλο του Ιδανικού αερίου και τη θέρμανσή του…
Ο Γιάννης είχε βάλει και ερωτήματα με τοξοβόλους επιταχυνόμενους και κανείς δεν έφερε αντίρρηση όταν καταλήξαμε πως η εσωτερική ενεέργεια ( η οποία αυτή -και μόνο αυτή – σχετίζεται με την θερμοκρασία ) υπολογίζεται σε κάθε περίπτωση ως προς το σύστημα του κέντρου Μάζας δηλαδή αδρανειακό.
Είτε ένα δοχείο με αέριο επιβραδυνθεί απότομα ( κρουστικά) είτε επιβραδυνθεί ημιστατικά ( πολύ αργά και ομαλά , παραμένοντας διαρκώς σε κατάσταση Ισορροπίας ) είναι παντελώς αδιαόρο … Διότι θα επιβραδυνθεί και η κίνηση του Κέντρου μαζας. Η εσωτερική ενέργεια και η θερμοκρασία παραμένει η ίδια .
Αλ(λο)ίμονο αν ήταν διαφορετικά τα πράγματα. Τότε αν βάζαμε στον πάγκο του εργαστηρίου ένα ακίνητο δοχείο με αέριο Ήλιο και του χώναμε και ένα θερμόμετρο να βλέπεουμε την θερμοκρασία του εμείς στο εργατήριο και ένας από τους Αστροναύτες του ΙSS που περνά πάνω από το εγαστήριο την ίδια στιγμή … Ε θα διαβάζαμε διαφορετικές θερμοκρασίες ; ! Όχι βεβαίως.
Η Κινητική Ενέργεια που μετρά κάθε παρατηρητής είναι σχετική δηλαδή είναι διαφορετική για κάθε παρατηρητή ( όχι οι μεταβολές της ) . Αλλά και τα ποσοστά μεταβολών είναι διαφορετικά για κάθε παρατηρητή. Η Εσωτερική Ενέργεια όμως ορίζεται μόνο ως το κέντρο μάζας και έχει ΜΙΑ τιμή ._
Να το πούμε και αλλιώς η v(rms) ΔΕΝ ΜΕΤΑΒΑΛΛΕΤΑΙ και αυτό στατιστικά αποδεικνυεται διότι εδώ δεν έχουμε συγκρούσεις μόνο με το μπροστά τοίχωμα αλλά με όλα τα τοιχώματα… διότι η τυχαία θερμική κίνηση είναι προς όλες τις κατευθύνσεις ( Το 0 Κ απόλυτη θερμοκρασία δεν παίζει και δεν θα μπω σε κουβέντα τώρα για το αν υπάρχει Ιδανικό αέριο σε απόλυτο μηδέν . Και πολύ καλά κάνει που το επισημαίνει το μποτάκι του ΚΥΡΓιάννη)
Άρη και βέβαια το έργο των εξωτερικών δυνάμεων πάνω στο δοχείο εκφράζει μόνο την μεταβολή της Κινητικής ενέργειας του δοχείου εενοούμενου ως μια οντότητα ως προς οποιονδήποτε παρατηρητή. Η Εσωτερική ενέργεια δεν μεταβάλλεται και αυτό είναι δεδομένο αν δεν συμβεί εσωτερικά αλλαγή του χημικού δυναμικού ή κάποια άλλη μεταβολή στο αέριο π.χ. μεταστοιχείωση . ( υπέθεσα ακλόνητα και αδιαβατικά τοιχώματα ) .
Ελπίζω η συζήτηση να μην φτάσει στο πόσο υπολόγισε ο Αϊνστάϊν ότι μειώνεται η μάζα ενός λίτρου νερού όταν την βάλω στην κατάψυξη …
Μια προσπάθεια απάντησης
Προφανώς η συνολική εξωτερική δύναμη που δέχεται το αέριο από τα τοιχώματα του δοχείου επιβραδύνει τι κέντρο μάζας του αερίου και με το έργο της μηδενίζει την μεταφορική κινητική του ενέργεια. Αυτή η ενέργεια μέσω του έργου της συνολικής δύναμης που ασκεί το αέριο στο δοχείο μεταβιβάζεται στο δοχείο και το αεροπλάνο και τελικά έχει την ίδια τύχη με την υπόλοιπη κινητική ενέργεια του αεροπλάνου: Θερμική ενέργεια μέσω του έργου των τριβών που σταματάνε το αεροπλάνο. Η υπόλοιπη ενέργεια του αερίου δηλ η εσωτερική του ενέργεια δεν επηρεάζεται. Οπότε δεν αλλάζει η θερμοκρασία του.