-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 19 ώρες, 5 λεπτά
Η κίνηση με την επίδραση δύο κάθετων δυνάμεων.
 Ένα σώμα μάζας 10kg ηρεμεί σε λείο οριζόντιο επίπεδο, στην αρχή ενός συστήματος οριζοντίων ορθογωνίων αξόνων x και y. Σε μια στιγμή t0=0, στο […]
Ένα σώμα μάζας 10kg ηρεμεί σε λείο οριζόντιο επίπεδο, στην αρχή ενός συστήματος οριζοντίων ορθογωνίων αξόνων x και y. Σε μια στιγμή t0=0, στο […] -
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 μέρα, 13 ώρες
Μέσα Μάνη: Γιατί είναι μια μοναδική γενετική «νησίδα» στην Ευρώπη
 Μια νέα γενετική μελέτη αποκαλύπτει ότι οι κάτοικοι της Μέσα Μάνης αποτελούν μια μοναδική γενετική «νησίδα» στην Ευρώπη, έναν από τους πιο ιδιαίτερους γ […]
Μια νέα γενετική μελέτη αποκαλύπτει ότι οι κάτοικοι της Μέσα Μάνης αποτελούν μια μοναδική γενετική «νησίδα» στην Ευρώπη, έναν από τους πιο ιδιαίτερους γ […] -
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 μέρες, 11 ώρες
Που να βάλουμε τη ράμπα;
 Έχουμε ένα κατακόρυφο ημικύκλιο ακτίνας 4 m. Θέλουμε από το σημείο Α που βρίσκεται στο επίπεδο του ημικυκλίου σε ύψος 8 m να οδηγήσουμε με μια λεία […]
Έχουμε ένα κατακόρυφο ημικύκλιο ακτίνας 4 m. Θέλουμε από το σημείο Α που βρίσκεται στο επίπεδο του ημικυκλίου σε ύψος 8 m να οδηγήσουμε με μια λεία […]-
Καλησπέρα Γιάννη. Το σημείο τομής τηςΑΟ με το ημικυκλιο;
-
Καλησπέρα Γιώργο.
Την χρονικά συντομότερη όχι την χωρικά συντομότερη. -
Γιάννη δεν το λες στην εκφώνηση για τον ελάχιστο χρόνο.
Έψαχνα να βρω γιατί να μην είναι οποιοδήποτε σημείο… -
Πιστεύω και χρονικά αφού η εφαπτομένη σε αυτό το σημείο κόβει τον άξονα ψ στον μικρότερη απόσταση από το Α.
-
Διονύση μου ξέφυγε.
Διόρθωσα τώρα, συμπληρώνω και την εκφώνηση της απάντησης. -
Γιώργο δεν έχουμε ίδιες επιταχύνσεις ούτε είναι στον ίδιο κύκλο.
-
Θα καθυστερήσω την ανάρτηση της απάντησης ώστε κάποιος φίλος να μπορέσει να ασχοληθεί. Ας ακολουθήσει την υπόδειξη αν θέλει.
-
Το σχήμα είναι απόλυτα ακριβές οπότε βρίσκεται η λύση με ένα χαρακάκι.
-
Σύμφωνα με την υπόδειξη t ΑΒ =t ΑΓ
Άρα όσο μικρότερο ΑΒ έχουμε τόσο μικρότερο χρόνο έχουμε
.
Στο σχήμα της άσκησης τώρα . Όσο μικρότερηαντιστοιχη διαδρομή στον ψ έχουμε τόσο μικρότερος χρόνος
Η διαδρομή στον Ψ είναι η υποτείνουσα του ορθογωνίου που σχηματίζεται από την ραμπα και τη κάθετο σε αυτή.
Η κάθετος αυτή τέμνει τον Ψ πιο κοντά στο Α όταν είναι εφαπτομένη στο σημείο τομής της ΑΟ με το ημικύκλιο. -
Όχι η υπόδειξη δεν λέει αυτό.
Λέει ότι δύο διαδρομές ΑΓ και ΑΖ είναι ισόχρονες αν τα Γ και Ζ ανήκουν στην ίδιο κύκλο που έχει κατακόρυφη διάμετρο.
Το σημείο που λες ανήκει σε κύκλο που έχει τη μικρότερη διάμετρο;
Όχι βέβαια.
Εξ άλλου βλέπεις από το απόλυτα ακριβές σχήμα ότι δεν είναι αυτό. -
Ναι πιστεύω ότι το σημείο που λέω είναι αυτο που έχει την μικρότερη διάμετρο( πάνω στον Ψ).
Το λέω από μνήμης επειδή δεν είμαι σπίτι και έτσι δεν χρησιμοποιώ μολύβι και χαρτί, αλλά έτσι πιστεύω. -
Γιώργο θα περιμένω και άλλους φίλους.
-
Καλησπέρα σας, ωραίο θέμα!
Αν δεν έχω λάθος . . .
Στο σχήμα συμπληρώνουμε το πάνω ημικύκλιο με το κάτω ημικύκλιο και έτσι έχουμε κύκλο με κέντρο Ο και ακτίνα 4m. Φέρνουμε την κατακόρυφη διάμετρο που περνά από το Ο. Τέμνει το πάνω ημικύκλιο στο σημείο Γ και το κάτω ημικύκλιο στο σημείο Δ. Φέρνουμε το τμήμα ΑΔ που τέμνει το πάνω ημικύκλιο σε ένα σημείο. Το σημείο αυτό είναι το Ε. -
Χρήστο με ένα χαρακάκι βρίσκεις το κέντρο γιατί το σχήμα είναι απολύτως ακριβές.
Η ακτίνα είναι σημαντικά μικρότερη από 4 m. -
Χρήστο θεώρησε άκυρο το σχόλιό μου.
Τώρα κατάλαβα.
Είναι πολύ σωστή η λύση σου και πιο όμορφη και σύντομη από τη δική μου.
Θα την αναρτήσω τώρα -
Η λύση αναρτήθηκε.
Βλέπουμε μια απόλυτη ταύτιση στο σημείο Ε με τη λύση του Χρήστου:
https://i.ibb.co/tTYTVsRY/87.png -
Με ενδιαφέρει η λύση σου Χρήστο.
Δύναμη σημείου; -
Ένα σχήμα:
-
https://i.ibb.co/8wMMbCF/page-0001-1.jpg
Να’σαι καλά Γιάννη! -
Χρήστο η λύση σου είναι κλάσεις καλύτερη από τη δική μου.
-
Σ’ ευχαριστώ πολύ Γιάννη, καλό σου βράδυ!
-
Καλησπερα Γιαννη. Επειδη ειμαστε στο Φορουμ και σου αρεσει η κουβεντουλα οπως και εμενα,εχω να πω τα εξης: Η ασκηση ειναι πολυ ωραια και αν δεν δοθει υποδειξη οτι μπορει να χρησιμοποιηθει το προβλημα της ισοχρόνου χορδης,μαλλον ειναι πολυ δυσκολο να σκεφτει κανεις αυτον τον τροπο. Μαλλον με με αναλυτικο τροπο θα το παει. Το προβλημα της ισοχρόνου χορδης το ειχα λυσει πιο παλια που το ειχε βαλει ο Μιλτος εδω.Ισόχρονη χορδήΚατοπιν ελυσα και το παρον προβλημα με τον ιδιο με τον δικο σου τρόπο,μεχρι το σημειο που γραφεις “ετσι τελειωσαμε” Στην συνεχεια χρειαζεται μια Ευκλειδεια κατασκευη την οποια διατυπωνω ως εξης:(Αναφερομαι στο σχημα που εχεις στα σχόλια)
Κατασκευη:Κατασκευαζω το σημειο Ζ και φερω την ΑΖ η οποια τεμνει το ημικυκλιο στο Ε.
Φερω την ευθεια την διερχομενη εκ των Ο,Ε η οποια τεμνει το ευθυγμαμμο τμημα ΑΒ στο Κ.
Γραφω κυκλο κεντρου Κ και ακτινας ΚΕ. Ο κυκλος Αυτος ειναι και ο ζητουμενος κυκλος.
Αποδειξη: Η διακεντρος ΟΚ εχει μηκος ισο με το αθροισμα των δυο ακτινων ,αρα το σημειο Ε ειναι σημειο επαφης των κυκλων. (ΟΕΔ).
Παρατηρηση: Eσυ Γιαννη απ οτι καταλαβα,εκτος αν κανω λαθος,δεν κανεις γεωμετρικη κατασκευη με την Ευκλειδεια εννοια,δηλαδη με κανονα και διαβητη. Βρισκεις με εξισωσεις το μηκος της ακτινας του ζητουμενου κυκλου και εν συνεχεία κατασκευαζεις ενα ευθυγραμμο τμημα το οποιο εχει μηκος ισο με την ακτινα του ζητουμενου κυκλου. Αυτο δεν ειναι Ευκλειδεια κατασκευη. Δεν εχεις κατασκευασει το κεντρο του. Δεν επιτρεπεται να μεταφερεις ευθυγραμμα τμηματα απο ενα μερος του επιπεδου σε ενα αλλο χρησιμοποιωντας εναν Ευκλειδειο διαβητη. Αυτοι ειναι οι κανονες. Ετσι αυτο που κανεις παραβιαζει τους κανονες μιας Ευκλειδειας κατασκευης.
Επιτρεπεται μονο να γραφεις κυκλους και να τραβας γραμμες και οταν σηκωσεις τον διαβητη απο το χαρτι,τοτε αυτος καταρρεει.
Η πιο πολιτισμενη μεθοδος επιλυσεως ενος προβληματος ειναι μια αγνη Ευκλειδεια κατασκευη.
Αν εχεις αντιρρηση πες μου να το συζητησουμε. -
Η τελευταία φράση:
Οι άλλοι απορούν:
-Πως το σκέφτηκε ο μπαγάσας: -
Ναι έχεις δίκιο.
Γι’ αυτό μου άρεσε πολύ περισσότερο η λύση του Χρήστου.
Επί τη ευκαιρία:
Η χρυσή τομή και η κλοπή:Πως κλέβεις δηλαδή και μετά το παρουσιάζεις εντελώς Ευκλείδια.
-
Καλησπέρα Γιαννη.
Επειδή θεωρησα ότι ο χωρικά συντομότερος δρομος είναι και ο χρονικά (απο μνημης) όταν επιασα μολύβι και χαρτί είδα ότι έχεις δικιο.
Σαν “απιστος Θωμας”ήθελα να το επιβαβαιωσω και μετρικά ,,, και το έκανα.
και αφου το ´κανα είπα να το ανεβασω:https://i.ibb.co/Psfv8sVx/SCAN-ian-50.png -
Πολύ όμορφη!
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 μέρες, 21 ώρες
Ένα πρωτόνιο εκτρέπεται από μαγνητικό πεδίο.
 Στο σχήμα βλέπουμε την τομή ενός ομογενούς μαγνητικού πεδίου στο επίπεδο της σελίδας, σχήματος τετράγωνου πλευράς α=0,4m, με ένταση Β=2∙10-4Τ, […]
Στο σχήμα βλέπουμε την τομή ενός ομογενούς μαγνητικού πεδίου στο επίπεδο της σελίδας, σχήματος τετράγωνου πλευράς α=0,4m, με ένταση Β=2∙10-4Τ, […]-
Ας δοκιμάσουμε λίγο, να δουλέψουμε με συντεταγμένες.
Μπορεί σε κάποιους μαθητές να δείξουν ενδιαφέρον… -
Καλημέρα Διονύση.
Ωραίο θέμα με αρκετή πρωτοτυπία!
(Μια οντότητα φορτωμένη με μια έννοια ή οντότητα (;) μπαίνει σε μια έννοια
και κάποια στιγμή βγαίνει …)Να είσαι καλά -
Καλό μεσημέρι Παντελή και σε ευχαριστώ για το σχολιασμό.
Όσον αφορά το έμμεσο σχόλιο περί οντότητας και έννοιας, να θυμίσω ένα παλιό σύνθημα;
“Συγκέντρωση δεν γίνεται χωρίς τον Αρκουδέα
αυτός δεν είναι άνθρωπος, είναι μια ιδέα” !
όπου Αρκουδέας, ο Αττικάρχης και στη συνέχεια αρχηγός της Αστυνομίας τη δεκαετία του 80…
Περισσότερα… -
Καλησπέρα Διονύση. Καλησπέρα Παντελή.
Πολύ καλή άσκηση Διονύση. -
Καλησπέρα Διονύση. Μόλις επιστρέψαμε στο σχολείο, με τη Γ τάξη, μετά από παρακολούθηση Καποδίστρια… Ο οποίος αν και ήταν οντότητα, παρουσιάστηκε ως έννοια. Ας μην επεκταθώ.
Ευτυχώς έπεσα στην ανάρτησή σου και ίσιωσα.
Πολύ όμορφη η χρήση των συντεταγμένων. Αισθητοποιεί τέλεια την τροχιά και την απόκλιση του πρωτονίου στο Μ.Π. Μάλιστα μου ήρθε και σχετική ιδέα… -
Διονύση Βλέπω μια σύμπλευση με τον Παντελή.
-
Καλό απόγευμα σε όλους.
Χριστόφορε, Ανδρέα και Γιάννη, σας ευχαριστώ για το σχολιασμό.
Ανδρέα, δεν είναι μόνο ο Αρκουδέας, ιδέα. Και ο Καποδίστριας είναι μια ιδέα 🙂
Γιάννη δεν άκουσα τη μάνα μου, που μου έλεγε να αποφεύγω τις κακές παρέες… 🙂 🙂 -
Καλημέρα σε όλους.
Μια μικρή παρατήρηση για το κλίμα της κουβέντας που υπάρχει στην παρούσα ανάρτηση.
Το χιούμορ μεταξύ μας είναι ωραίο και δίνει ζωντάνια, αλλά όταν μια ιδέα αντιμετωπίζεται με ειρωνεία στα όρια του χλευασμού— ακόμη και καλοπροαίρετη — οι νεότεροι ή πιο διστακτικοί αναγνώστες μπορεί να το εκλάβουν ως μήνυμα ότι δεν είναι ασφαλές να καταθέτουν απορίες ή διαφορετικές οπτικές.
Και είναι κρίμα, γιατί η Φυσική κερδίζει όταν ανοίγουμε χώρο για ερωτήματα, όχι όταν τα αποθαρρύνουμε άθελά μας.
Δεν είναι κακό να λέμε ξεκάθαρα ότι μια άποψη είναι λάθος. Αρκεί να το κάνουμε με επιχειρήματα και όχι με ειρωνείες. Έτσι βοηθάμε τη συζήτηση να μένει γόνιμη.
Το λέω με διάθεση να κρατήσουμε φιλόξενες τις συζητήσεις στο φ-ylikonet.
-
Ωραία ερώτηση — και σπάνια συζητιέται όσο θα έπρεπε.
Ένας διάλογος πάνω σε επιστημονικό θέμα είναι γόνιμος όταν δεν είναι απλώς ανταλλαγή απόψεων, αλλά διαδικασία κοινής αναζήτησης της αλήθειας. Αυτό φαίνεται από μερικά βασικά σημάδια:1. Στόχος είναι η κατανόηση, όχι η “νίκη”Αν οι συμμετέχοντες προσπαθούν να καταλάβουν το φαινόμενο καλύτερα — ακόμα κι αν χρειαστεί να αλλάξουν άποψη — τότε ο διάλογος προχωρά.
Αν ο στόχος είναι «να αποδείξω ότι έχω δίκιο», σταματά η επιστήμη και αρχίζει η ρητορική.2. Γίνονται σαφείς οι όροι και οι παραδοχέςΠολλές “διαφωνίες” είναι απλώς διαφορετικοί ορισμοί.
Γόνιμος διάλογος σημαίνει:- ξεκαθαρίζουμε τι εννοούμε με βασικές έννοιες
- λέμε ανοιχτά ποιες παραδοχές κάνουμε
- Έτσι αποφεύγεται να μιλάμε για διαφορετικά πράγματα νομίζοντας ότι μιλάμε για το ίδιο.
3. Υπάρχει αναφορά σε δεδομένα, όχι μόνο σε απόψειςΗ επιστήμη βασίζεται σε:
- παρατηρήσεις
- πειράματα
- μετρήσεις
- δημοσιευμένα ευρήματα
Όταν ο διάλογος γυρίζει μόνο σε “μου φαίνεται λογικό”, γίνεται φιλοσοφική κουβέντα — που μπορεί να είναι ενδιαφέρουσα, αλλά δεν είναι επιστημονική τεκμηρίωση.
4. Υπάρχει διανοητική ταπεινότηταΦράσεις όπως:
- «Μπορεί να κάνω λάθος»
- «Δεν το είχα σκεφτεί έτσι»
- «Αυτό αλλάζει την εικόνα»
είναι δείκτες ποιότητας, όχι αδυναμίας. Χωρίς τη δυνατότητα αναθεώρησης, δεν υπάρχει επιστημονική πρόοδος.
5. Γίνεται διάκριση ανάμεσα σε δεδομένα και ερμηνείαΔύο επιστήμονες μπορεί να συμφωνούν στα δεδομένα αλλά να διαφωνούν στην ερμηνεία.
Ο γόνιμος διάλογος:- αναγνωρίζει τι είναι παρατήρηση
- τι είναι μοντέλο
- τι είναι υπόθεση
Έτσι η διαφωνία γίνεται δημιουργική αντί για χαοτική.
6. Υπάρχει χρόνος για σκέψη (όχι μόνο άμεση αντίδραση)Η καλή επιστημονική συζήτηση έχει:
- παύσεις
- αναστοχασμό
- διάθεση να διαβαστεί κάτι και να επανέλθει η κουβέντα
Η βιασύνη γεννά επιφανειακές απαντήσεις.
7. Στο τέλος όλοι ξέρουν κάτι περισσότεροΑκόμα κι αν δεν υπάρξει συμφωνία, ο διάλογος είναι γόνιμος όταν:
- έχουν ξεκαθαρίσει τα σημεία διαφωνίας
- έχουν προκύψει νέες ερωτήσεις
- έχει βελτιωθεί η κατανόηση του προβλήματος
Η επιστήμη προχωρά συχνά περισσότερο με καλύτερες ερωτήσεις παρά με τελικές απαντήσεις.
Με μια φράση:
https://i.ibb.co/spVz2yPC/3-1.jpg Γόνιμος επιστημονικός διάλογος είναι αυτός που αυξάνει τη συλλογική κατανόηση, όχι τα εγώ των συμμετεχόντων. -
Έθεσα μια ερώτηση στο ChatGpt και πήρα την απάντηση:
Πότε ένας διάλογος πάνω σε ένα επιστημονικό θέμα είναι γόνιμος;
Ωραία ερώτηση — και σπάνια συζητιέται όσο θα έπρεπε.
Ένας διάλογος πάνω σε επιστημονικό θέμα είναι γόνιμος όταν δεν είναι απλώς ανταλλαγή απόψεων, αλλά διαδικασία κοινής αναζήτησης της αλήθειας. Αυτό φαίνεται από μερικά βασικά σημάδια:1. Στόχος είναι η κατανόηση, όχι η “νίκη”Αν οι συμμετέχοντες προσπαθούν να καταλάβουν το φαινόμενο καλύτερα — ακόμα κι αν χρειαστεί να αλλάξουν άποψη — τότε ο διάλογος προχωρά.
Αν ο στόχος είναι «να αποδείξω ότι έχω δίκιο», σταματά η επιστήμη και αρχίζει η ρητορική.2. Γίνονται σαφείς οι όροι και οι παραδοχέςΠολλές “διαφωνίες” είναι απλώς διαφορετικοί ορισμοί.
Γόνιμος διάλογος σημαίνει:- ξεκαθαρίζουμε τι εννοούμε με βασικές έννοιες
- λέμε ανοιχτά ποιες παραδοχές κάνουμε
- Έτσι αποφεύγεται να μιλάμε για διαφορετικά πράγματα νομίζοντας ότι μιλάμε για το ίδιο.
3. Υπάρχει αναφορά σε δεδομένα, όχι μόνο σε απόψειςΗ επιστήμη βασίζεται σε:
- παρατηρήσεις
- πειράματα
- μετρήσεις
- δημοσιευμένα ευρήματα
Όταν ο διάλογος γυρίζει μόνο σε “μου φαίνεται λογικό”, γίνεται φιλοσοφική κουβέντα — που μπορεί να είναι ενδιαφέρουσα, αλλά δεν είναι επιστημονική τεκμηρίωση.
4. Υπάρχει διανοητική ταπεινότηταΦράσεις όπως:
- «Μπορεί να κάνω λάθος»
- «Δεν το είχα σκεφτεί έτσι»
- «Αυτό αλλάζει την εικόνα»
είναι δείκτες ποιότητας, όχι αδυναμίας. Χωρίς τη δυνατότητα αναθεώρησης, δεν υπάρχει επιστημονική πρόοδος.
5. Γίνεται διάκριση ανάμεσα σε δεδομένα και ερμηνείαΔύο επιστήμονες μπορεί να συμφωνούν στα δεδομένα αλλά να διαφωνούν στην ερμηνεία.
Ο γόνιμος διάλογος:- αναγνωρίζει τι είναι παρατήρηση
- τι είναι μοντέλο
- τι είναι υπόθεση
Έτσι η διαφωνία γίνεται δημιουργική αντί για χαοτική.
6. Υπάρχει χρόνος για σκέψη (όχι μόνο άμεση αντίδραση)Η καλή επιστημονική συζήτηση έχει:
- παύσεις
- αναστοχασμό
- διάθεση να διαβαστεί κάτι και να επανέλθει η κουβέντα
Η βιασύνη γεννά επιφανειακές απαντήσεις.
7. Στο τέλος όλοι ξέρουν κάτι περισσότεροΑκόμα κι αν δεν υπάρξει συμφωνία, ο διάλογος είναι γόνιμος όταν:
- έχουν ξεκαθαρίσει τα σημεία διαφωνίας
- έχουν προκύψει νέες ερωτήσεις
- έχει βελτιωθεί η κατανόηση του προβλήματος
Η επιστήμη προχωρά συχνά περισσότερο με καλύτερες ερωτήσεις παρά με τελικές απαντήσεις.
Με μια φράση:
https://i.ibb.co/spVz2yPC/3-1.jpg Γόνιμος επιστημονικός διάλογος είναι αυτός που αυξάνει τη συλλογική κατανόηση, όχι τα εγώ των συμμετεχόντων. -
Καλημέρα Ανδρέα ,καλημέρα Διονύση.
Ελπίζω πως το αρχικό σχόλιο μου στην παρούσα ανάρτηση του Διονύση
(Μια οντότητα φορτωμένη με μια έννοια ή οντότητα (;) μπαίνει σε μια έννοια
και κάποια στιγμή βγαίνει …)
δεν υποκρύπτει ειρωνεία παρά μόνο ένα (;) για το φορτίο, με το δικό μου ,άχρωμο ίσως, να το πω χιούμορ.
Αν διακρίνονται ίχνη τέτοιας ειλικρινά ζητώ συγνώμη και εγώ. -
Καλημέρα Ανδρέα.
«Δεν είναι κακό να λέμε ξεκάθαρα ότι μια άποψη είναι λάθος. Αρκεί να το κάνουμε με επιχειρήματα και όχι με ειρωνείες. Έτσι βοηθάμε τη συζήτηση να μένει γόνιμη.»
Έχει και άλλες προϋποθέσεις μια συζήτηση για να είναι γόνιμη.
Πρώτα – πρώτα να είναι συζήτηση, να διατυπώνονται απόψεις και θέσεις με ξεκάθαρο τρόπο ώστε οι συμμετέχοντες να είναι φανερό για τι πράγμα μιλούν και πού στοχεύουν. Αλλά ταυτόχρονα οι απόψεις αυτές να στοχεύουν στην αναζήτηση της αλήθειας και όχι στην επιβολή μιας «αλήθειας» που ερχόμαστε να επιβάλλουμε στους συνομιλητές μας, αλλά και να την διδάξουμε, μέσω του δικτύου και στους μαθητές που μας παρακολουθούν
Μέρες τώρα αρνείσαι να ακούσεις ΕΝΑ, έστω ΕΝΑ επιχείρημα, από αυτά που οι φίλοι εδώ διατύπωσαν, ενάντια στην αρχική σου ανάρτηση.
Μια ανάρτηση που ο διαχειριστής του δικτύου, σου ζήτησε να μεταφέρεις στο φόρουμ. Τι πιο απλό και δημοκρατικό; Να συζητήσουμε ό,τι θέλουμε, αλλά να φαίνεται ότι συζητάμε και δεν δίνουμε στα παιδιά υλικό απαραίτητο για την πρόοδό τους. Ότι εδώ συζητάμε και προβληματιζόμαστε. Δεν διδάσκουμε από καθέδρας την απόλυτη αλήθεια. Και συ το αρνήθηκες πεισματικά!!!
Στηρίζεσαι στην ιδιαίτερα δημοκρατική στάση του Αποστόλη για να κάνεις το δικό σου και να επιβάλεις τη θέση σου, καπελώνοντας το δίκτυο και επιβάλλοντας μια λογική.
Και όχι μόνο αυτό, αλλά μετά από 46 σχόλια, αφήνεις την ανάρτηση για το φως ξεκινώντας μια νέα, με το ίδιο περιεχόμενο, ξανά απευθύνοντάς την στους μαθητές. Και ξανά αρνείσαι να την θεωρήσεις συζήτηση.
Την θεωρείς απόλυτη αλήθεια, έτοιμη για να διδαχτεί! Καμιά διάθεση διαλόγου και προβληματισμού.
Μετά από όλα αυτά, ο διάλογος εκφυλίζεται και έρχεται το χιούμορ να χαλαρώσει μια ήδη τεταμένη ατμόσφαιρα…
Ξέφυγε σε ειρωνεία;
Αν αυτό έγινε ζητάω συγνώμη προσωπικά, για την δική μου εκτροπή που ίσως παρέσυρε και άλλους φίλους σε ανάλογη ανάλαφρη αντιμετώπιση. -
Διονύση αρκούσε η τελευταία φράση σου.
Για όσα αναφέρεις πριν από αυτή, επειδή αφορούν την ανάρτησή μου ΘΕΜΑ Α και Β: Η έννοια φως – Υλικό Φυσικής – Χημείας θα γράψω τα σχόλιά μου κάτω από αυτή.
Σχετικά με το επόμενο σχόλιό σου, συμφωνώ με τη απάντηση του ChatGpt.
-
Παντελή καλημέρα
Με λίγα λόγια και σταράτα διέλυσες την παρεξήγηση.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 3 μέρες, 12 ώρες
Οι τρεις δρομείς.
 Τρεις δρομείς τρέχουν σε αγώνα 1.000 μ. Τρέχουν σε κάθε περίπτωση με την ίδια και σταθερή ταχύτητα ο καθένας. Για να τερματίσει ο Α ταυτόχρ […]
Τρεις δρομείς τρέχουν σε αγώνα 1.000 μ. Τρέχουν σε κάθε περίπτωση με την ίδια και σταθερή ταχύτητα ο καθένας. Για να τερματίσει ο Α ταυτόχρ […]-
Βρίσκουμε το πρόβλημα στο Mind your decisions.
Το λύνει αλγεβρικά. -
Καλησπέρα Γιάννη. Είναι ένα εύκολο πρόβλημα και βγαίνει αμέσως.Παρεπιπτοντως έκανα την 1η λύση. Ενδιαφέρουσες και οι άλλες. Πιστεύω ότι θα υπάρχουν και αρκετές άλλες λύσεις.
-
Καλησπέρα Γιώργο.
Ναι υπάρχουν πολλές λύσεις κυρίως αλγεβρικές.
Ένα πιθανό λάθος εντοπίζει το βίντεο στην αρχή. Να πεις ότι η διαφορά πρέπει να είναι 19 μέτρα. -
Ναι αυτή φαίνεται ότι είναι η παγίδα. Αλλά το ότι δίνει 69 αντί κάτι στρογγυλό (π.χ 70 ) όπως το 50 φαίνεται από την ανάγνωση ότι είναι παγίδα.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 4 μέρες, 19 ώρες
Μετρήσεις σε κύκλωμα με ιδανικά όργανα…
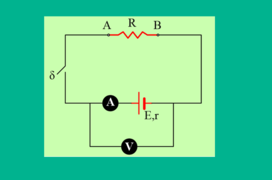 Δίνεται το κύκλωμα του διπλανού σχήματος, όπου η πηγή έχει ΗΕΔ Ε=10V και εσωτερική αντίσταση r=1Ω, ενώ μεταξύ των σημείων Α και Β μπορούμε να συνδ […]
Δίνεται το κύκλωμα του διπλανού σχήματος, όπου η πηγή έχει ΗΕΔ Ε=10V και εσωτερική αντίσταση r=1Ω, ενώ μεταξύ των σημείων Α και Β μπορούμε να συνδ […]-
Καλό μήνα σε όλους.
Αφιερωμένη στους συναδέλφους που διδάσκουν φυσική γ.π. στην Β΄ Λυκείου και επιμένουν να κάνουν μάθημα… -
Καλημέρα Διονύση και καλό μήνα.
Ο “μεγεθυντικός φακός” των ερωτήσεων που θέτεις στοχευμένα, δείχνει το δρόμο των απαντήσεων, χωρίς να αποκαλύπτει τη λύση , συμβάλλοντας στην κατανόηση του φαινομένου!
Βασικά πράγματα που πρέπει να διδάσκονται, προκειμένου να αφομοιώσει ο μαθητής βασικές έννοιες !
Τα θέματα που θέτεις προσομοιάζονται με ..τον παππού που πιάνει το εγγόνι του και του δείχνει τα αμπελοχώραφά του!
Νάσαι καλά. -
Καλημέρα Διονύση. Πολύ καλή. Οι μαθητές μαθαίνουν τη φυσική σημασία της ΗΕΔ και της εσωτερικής αντίστασης. Πραγματοποιείται και στο εργαστήριο αλλά και με την προσομοίωση του Phet. Αυτά μαθαίνονται στη Β΄Λυκείου και όχι στη Γ΄, όταν κάνουμε το νόμο Biot-Savart. Έχει πετάξει το πουλάκι. Ο διδάσκοντας πρέπει να κάνει άθλο να το εξηγήσει και να πείσει τους μαθητές.
-
Καλημέρα Διονύση . ‘Ομορφη και προπάντως διδακτική, όπως πάντα.
Ισως θα έπρεπε να αναφερθεί στο πρώτο ερώτημα και η απάντηση “η εξωτερική αντίσταση R να είναι πολύ μεγάλη , τόσο ώστε η ενταση του ρεύματος που δείχνει το αμπερόμετρο να είναι πολυ μικρότερη της μικροτερης ενδειξης στην κλιμακα του”, με σκοπό να γίνει κάποια συζητηση με αυτό (περισσότερο εργαστηριακού ενδιαφέροντος). -
Καλό απόγευμα συνάδελφοι.
Πρόδρομε, Ανδρέα και Γιώργο σας ευχαριστώ για το σχολιασμό.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 6 μέρες, 7 ώρες
Η ισχύς της αρχής της ανεξαρτησίας των κινήσεων.
 Ας δούμε τι λέει πότε ισχύει και πότε όχι. Συνέχεια:
Ας δούμε τι λέει πότε ισχύει και πότε όχι. Συνέχεια:-
Καλημερα Γιαννη.Θα ηθελα να ρωτησω κατι. Ποια ειναι η διατυπωση της περιβοητης αρχης ανεξαρτησιας των κινησεων?
Στην οριζοντια βολη η x κινηση και η y κινηση ειναι ανεξαρτητες μεταξυ τους?
Ναι διοτι η παραβολικη κινηση αναλυεται σε μια ευθυγραμη ομαλη στον x και μια ευθυγραμμη ομαλα επιταχυνομενη στον y και αν εφαρμοσουμε πρωτα την μια και μετα την αλλη βρισκουμε το σωμα στο σωστο σημειο.
Στην ομαλη κυκλικη κινηση οπως στον δορυφορο του μικρου πριγκιπα,η η x κινηση και η y κινηση ειναι ανεξαρτητες μεταξυ τους?
Ναι διοτι η ομαλη κυκλικη κινηση αναλυεται σε μια ΑΑΤ στον x και μια άλλη ΑΑΤ στον y και αν εφαρμοσουμε πρωτα την μια και μετα την αλλη βρισκουμε το σωμα στο σωστο σημειο.
Μαθηματικα ομως αν απαλειψεις τον χρονο απο τις δυο ανεξαρτητες κινησεις x(t) και y(t) βρισκεις σχεση μεταξυ x και y αρα οι δυο κινησεις ποτέ δεν ειναι ανεξαρτητες μεταξυ τους.
Για να καταλαβω το εννοει κανεις οταν λεει αρχη ανεξαρτησιας των κινησεων και οταν λεει οτι η αρχη αυτη ισχυει οταν δυο κινησεις ειναι ανεξαρτητες μεταξυ τους θελω σαφεις μαθηματικους ορισμους αυτων των εννοιων.
Εχω διαβασει τον Ανδρεα:
http://users.sch.gr/kassetas/yPrincipioIndipendenza3.htm
και δεν εχω καταλαβει τι ακριβως εννοει.
Θελω στην πρωτη σειρα να δω ορισμους τους οποιους δεν εχει.
Επισης διαβαζω το παραδειγμα σου με τον του πλανητάκο του μικρού πρίγκηπα,που το εχω δει και σε αναρτηση σου του 2018 και παλι δεν καταλαβαινω γιατι σε αυτην την περιπτωση η αρχη ανεξαρτησιας καταρριπτεται. Τι θα πει κλεινω το βαρυτικο πεδιο? Σε ποιες κινησεις αναλυουμε την κινηση του μπαλακιου-δορυφορου οι οποιες δεν ειναι ανεξαρτητες?Στον εφαπτομενικο αξονα το σωμα δεν κανει ΕΟΚ πως το παιρνεις να κανει ΕΟΚ?
Στην οριζοντια βολη το βαρος που ειναι και η μοναδικη δυναμη δεν εχει συνιστωσα στον x αλλα μονο στον y και για αυτολεμε οτι οι κινησεις στους x,y ειναι ανεξαρτητες?
Τελικα η αρχη της ανεξαρτησιας ειναι αρχη της κινηματικης ή της δυναμικης?Χρειαζομαι ορισμους πριν απο οτιδηποτε αλλο για να καταλαβαινω τα υπολοιπα και νομιζω και καθε αναγνωστης.Οταν λεμε κατι καινουργιο, δεν θεωρειται τιποτα δεδομενο χρειαζεται θεμελιωση.
Τα πιο πανω τα γραφω ως αποριες και οχι ως παρατηρησεις. Nα υποθεσεις οτι ενας μαθητης σου σου κανει αυτες τις ερωτησεις και περιμενει να τον ξεμπλεξεις 🙂 -
Καλημέρα Γιάννη, βλέπω να επιμένεις να διευκρινίσεις την αρχή!
Ας κάνω μια προσπάθεια να δώσω μια σύντομη απάντηση στον Κωνσταντίνο (καλημέρα Κωνσταντίνε), χωρίς αυτό να σημαίνει ότι τα ερωτήματα δεν περιμένουν δικές σου απαντήσεις.
Η διατύπωση της αρχής μιλάει για δυο κινήσεις ανεξάρτητες μεταξύ τους.
Ας το διερευνήσουμε σε κάποιες περιπτώσεις.
Στην οριζόντια βολή (εύκολο…) Το πόσο πέφτει το σώμα σε ορισμένο χρόνο, εξαρτάται από την ταχύτητα στον οριζόντιο άξονα; Όχι. Μήπως η ταχύτητα μια στιγμή στον άξονα x εξαρτάται από το αν πέφτει ή όχι και από την θέση ή την ταχύτητα στον άξονα y; Ξανά όχι. Έχουμε δηλαδή δύο κινήσεις ανεξάρτητες.
Πάμε στην ομαλή κυκλική κίνηση με την ανάλυση σε δύο κάθετες αρμονικές ταλαντώσεις. Η μία ταλάντωση εξαρτάται από την άλλη και με ποιο τρόπο; Είναι προφανές ότι δεν υπάρχει καμιά εξάρτηση… Ξανά ανεξάρτητες κινήσεις.
Πάμε στον πλανητάκο του Γιάννη ή στην μαθήτρια του Ανδρέα. Η σκέψη είναι να πάρουμε δύο κινήσεις, μια ΕΟΚ στη διεύθυνση της αρχικής ταχύτητας, όπου μεταφέρει το σώμα σε κάποιο σημείο μακριά από το σημείο εκτόξευσης και μια ελεύθερη πτώση στη συνέχεια που θα το επαναφέρει στην επιφάνεια.
Είναι ανεξάρτητες αυτές οι δύο κινήσεις;
Ας υποθέσουμε ότι το σώμα τις εκτελεί, πρώτα τη μία και ύστερα την άλλη:
1) Πρώτα λόγω ταχύτητας, φτάνει στο σημείο Α και στη συνέχεια πέφτει φτάνοντας στο σημείο Β, του σχήματος.https://i.ibb.co/v6HMWM2M/333.png
2) Αν αντιστρέψουμε τη σειρά των δύο κινήσεων; Αφήνουμε πρώτα το σώμα να “πέσει”. Δεν θα πάει πουθενά. Οπότε αν στη συνέχεια εκτελέσει την ΕΟΚ θα βρεθεί όχι στο σημείο Β, αλλά το σημείο Α.
Συνεπώς έχουμε διαφορετικές τελικές θέσεις ανάλογα με τη σειρά εκτέλεσης των δύο κινήσεων, πράγμα που μας λέει ότι οι δυο κινήσεις δεν είναι ανεξάρτητες… -
Kαλημερα Διονυση. Πρεπει να υπαρχει ενα θεωρητικο κριτηριο,το οποιο στην ουσια να ταυτιζεται με τον ορισμο δυο ανεξαρτητων κινησεων. Πως οριζονται αυτες οι κινησεις? Στην περιπτωση ης μαθητριας ο ΟΑ ειναι σταθερος αξονας ενω ο ΑΒ ειναι μεταβλητος αξονας. Μπορω να βρω πολλες περιπτωσεις και αλλων αξονων ωστε αν το σωμα εκτελεσει διαδοχικα τις κινησεις να μην βρεθει τελικα στο σωστο σημειο.
-
Κωνσταντίνε, στην περίπτωση του “πλανητάκου” οι δύο “κινήσεις” ορίζονται με βάση:
1) την αρχική ταχύτητα
2) την ασκούμενη δύναμη (εδώ το βάρος).
Αν είχαμε μόνο το ένα ή μόνο το άλλο 🙂 -
Αν κανουμε το ιδιο στην πλαγια βολη μεσα σε ομογενες πεδιο βαρυτητας δηλαδη αν παρουμε ΕΟΚ και ελευθερη πτωση τοτε αν τα κανουμε διαδοχικα,τοτε βρισκουμε το σωμα στο σωστο σημειο.Τοτε λεμε οτι οι δυο κινησεις ειναι ανεξαρτητες? Υπαρχει καποιο θεωρητικο κριτηριο το οποιο λογικα πρεπει να ειναι καποιος ορισμος,που να μας επιτρεπει να αποφανθουμε πριν κανουμε τον ελεγχο της διαδοχικης εφαρμογης των δυο κινησεων?
Και παντα πρεπει να υπαρχει μια αρχικη ταχυτητα που καθοριζει τον εναν αξονα και μια δυναμη που καθοριζει τον αλλο? Για αυτο ειπα οτι πριν απο οτιδηποτε χρειαζονται ορισμοι.
Νομιζω οτι με σαφη ορισμο των α) ανεξαρτητων κινησεων και β) Διατυπωση ης αρχης ανεξαρτησιας των κινησεων,ολα μετα γινονται πιο απλα.
Υπ οψιν οτι ολα αυτα τα εκφραζω ως αποριες και οχι ως παρατηρησεις,γνωριζοντας ηδη τις απαντησεις. -
Καποιες φορες βεβαια ενας μαθητης ρωταει κατι και εμεις οι καθηγητες δυσκολευομαστε να καταλαβουμε τι ειναι αυτο που δεν εχει καταλαβει.
Δεν ξερω μηπως ειναι τετοια και η περιπτωση μας με αυτα που ρωταω 🙂 -
Η αρχή της ανεξαρτησίας των κινήσεων λέει ότι αν x = f_1(t) και y = f_2(t), τότε (διάνυσμα) r = x* (διάνυσμα) x_0 + y*(διάνυσμα) y_0.
-
Κωνσταντίνε, αν ψάχνεις για ορισμό, τι λες να δούμε τι σημαίνει “ανεξάρτητες” κινήσεις; Ανεξάρτητες γλωσσικά, σημαίνει ότι η μια δεν επηρεάζει και δεν εξαρτάται από την άλλη…
Ας έρθουμε λοιπόν πάλι στο “πλανητάκο”. Το βάρος του σώματος κατά την πτώση, εξαρτάται από το ύψος που βρίσκεται από την επιφάνεια, που αυτό με τη σειρά του συνδέεται με την αρχική ταχύτητα εκτόξευσης. Δηλαδή η ταχύτητα (της μιας κίνησης) καθορίζει την επιτάχυνση της άλλης κινησης.
Ας το δούμε αυτό στην περίπτωση, κάτι ανάλογου.
Ένα φορτισμένο σωματίδιο εκτελεί ΟΚΚ σε ΟΜΠ, όπως στο σχήμα.https://i.ibb.co/FbnYnZdg/434.png
Αν πάρουμε δύο “κινήσεις” η μία λόγω ταχύτητας και η άλλη λόγω δύναμης, βλέπουμε ότι η δύναμη εξαρτάται από την ταχύτητα. Συνεπώς η επιτάχυνση της μιας κίνησης (και όλα τα επόμενα, υ, Δx…) εξαρτώνται από την ταχύτητα της άλλης κίνησης.
Δυο κινήσεις που η μία εξαρτάται από την άλλη. Μη ανεξάρτητες. -
Καλημέρα Κωνσταντίνε και Διονύση.
Ωραίο το παράδειγμα του Διονύση με τον πλανητάκο.
Κωνσταντίνε η αρχή της ανεξαρτησίας ισχύει σε κάθε περίπτωση διότι απορρέει από την αντιμεταθετική ιδιότητα της άθροισης διανυσμάτων και τη χρήση παρατηρητών. Έτσι το ερώτημα:
-Πότε ισχύει η αρχή της ανεξαρτησίας των κινήσεων;
είναι ρητορικό.
Υπάρχει μια παρεξήγηση που ταυτίζει την αρχή της ανεξαρτησίας με ένα χειρισμό:
-Κλείσε το βαρυτικό πεδίο και άσε το σώμα να κινηθεί για χρόνο t. Εκεί που θα πάει ακινητοποίησέ το και άνοιξε το διακόπτη του βαρυτικού πεδίου. Άσε το σώμα να πέσει για χρόνο t και έχεις βρει την τελική θέση.
Η παραπάνω συνταγή δεν είναι η αρχή της ανεξαρτησίας των κινήσεων και πολλές φορές αποτυγχάνει.
Η αρχή ουδέποτε αποτυγχάνει αν εφαρμοστεί σωστά. Φάνηκε αυτό στο παράδειγμα της μαθήτριας.
Όμως η λανθασμένη συνταγή σε κάποιες περιπτώσεις επιτυγχάνει. Ποιες;
Αυτό διερευνάται στο παρόν πόνημα.
Επιτυγχάνει π.χ. στην βολή με αντίσταση αέρα -b.υ αλλά όχι στην περίπτωση -b.υ^2.
Η αρχή επιτυγχάνει και στην περίπτωση -b.υ^2 διότι η Κινηματική αδιαφορεί για τις δυνάμεις.
Η αρχή της ανεξαρτησίας επιτυγχάνει ακόμα και στις στροφές ή στην κίνηση σε μη Ευκλείδειους χώρους.
Η συνταγή αποτυγχάνει στις στροφές και στην κίνηση σε μη Ευκλείδειους χώρους εκτός αν εφαρμοστεί τοπικά. Αποτυγχάνει διότι δεν είναι η αρχή αλλά μια λανθασμένη εφαρμογή της. Μια εφαρμογή που διδάσκεται στην τάξη όπου δεν θέλουμε να μπλέξουμε παρατηρητές.
Μια επιπόλαια εφαρμογή που όμως φάνηκε χρήσιμη στην απόδειξη του Αλεξόπουλου για την Coriolis και σ’ αυτήν για την κεντρομόλο.
Είμαι εκ των οπαδών της αρχής της ανεξαρτησίας των κινήσεων και όχι πολέμιος. -
Καλημέρα κύριε Βάρβογλη.
Γράφετε την (προφανώς ορθή) Καρτεσιανή περιγραφή.
Το ότι μια επίπεδη κίνηση έχει δύο συντεταγμένες.
Μια διατύπωση της αρχής της ανεξαρτησίας των κινήσεων είναι:
-Η μετατόπιση ενός σώματος ως προς παρατηρητή Α είναι το διανυσματικό άθροισμα της μετατόπισης του σώματος ως προς παρατηρητή Β και της μετατόπισης του Β ως προς τον Α.Απορρέει από την αντιμεταθετική ιδιότητα στην άθροιση διανυσμάτων. Δεν εφαρμόζεται εύκολα σε περιπτώσεις στροφών που δεν είναι διανύσματα.
Εφαρμόζεται εύκολα σε περιπτώσεις απειροστών στροφών που είναι διανύσματα. -
Κωνσταντίνε γράφεις:
Επισης διαβαζω το παραδειγμα σου με τον του πλανητάκο του μικρού πρίγκηπα,που το εχω δει και σε αναρτηση σου του 2018 και παλι δεν καταλαβαινω γιατι σε αυτην την περιπτωση η αρχη ανεξαρτησιας καταρριπτεται.
Δεν είπα ότι καταρρίπτεται. Το αντίθετο λέω ότι έχει καθολική ισχύ.
Είπα ότι δεν δουλεύει η συνταγή “Κλείσε τον διακόπτη του πεδίου και…”.
Ενώ η συνταγή δουλεύει στην διάβαση του ποταμού και στις βολές.Στην ανάρτηση με την άσκηση των Δεσμών φαίνεται άλλη μια κακή εφαρμογή της συνταγής και όχι φυσικά μια απόπειρα να καταρριφθεί κάτι που είναι σωστό όπως η αρχή αυτή.
-
Τι σημαίνει “ανεξάρτητες κινήσεις”;
Η Vx δεν εξαρτάται από το y και η Vy δεν εξαρτάται από το x. -
Φυσικά ισχύει πάντα είτε οι κινήσεις είναι ανεξάρτητες είτε όχι.
Αυτό λέω, ότι η αρχή ισχύει πάντα. Η αρχή δεν κάνει λάθος.
Κάποιες φορές κάνει λάθος μια συνταγή που κακώς ταυτίζεται με την αρχή.
Η συνταγή που λέει:
-Κλείσε το βαρυτικό πεδίο και άσε το σώμα να κινηθεί για χρόνο t. Εκεί που θα πάει ακινητοποίησέ το και άνοιξε το διακόπτη του βαρυτικού πεδίου. Άσε το σώμα να πέσει για χρόνο t και έχεις βρει την τελική θέση.Η συνταγή αυτή:
- Δεν είναι η υπό συζήτησιν αρχή.
- Είναι γενικώς λανθασμένη.
- Επιτυγχάνει κάποιες φορές όταν οι κινήσεις είναι ανεξάρτητες με την έννοια ότι οι x εξισώσεις δεν έχουν το y και οι y εξισώσεις δεν έχουν το x.
- Επιτυγχάνει σε μικρές μετατοπίσεις (παράδειγμα η απόδειξη Αλεξόπουλου για την Coriolis).
-
Για τον κύριο Κυριακόπουλο.
Η διανυσματική σχέση που γράφετε ισχύει πάντα, είτε οι κινήσεις είναι ανεξάρτητες είτε όχι. Ανεξάρτητες κινήσεις έχουμε αν μπορούνε να διαχωρίσουμε τη διαφορική εξίσωση της κίνησης σε 2 (ή 3) ανεξάρτητες διαφορικές εξισώσεις. Αυτό εννοώ γράφοντας x = f(t). Ότι η κίνηση ως προς x εξαρτάται ΜΟΝΟ από τον χρόνο και όχι από τις τιμές των y (και z). -
Επίσης κύριε Βάρβογλη να γενικεύσω κάτι που γράφετε για το x=f1(t) και y=f2(t).
Θα είχαμε ανεξαρτησία ακόμα και αν Vx=f1(x,t) και Vy=f2(y,t).
Τότε η (γενικώς λανθασμένη) συνταγή επιτυγχάνει.
Η αρχή επιτυγχάνει σε κάθε περίπτωση Vx=f1(x,y,t) και Vy=f2(x,y,t).
Επιτυγχάνει διότι είναι σωστή. -
Aρα η αρχη της ανεξαρτησιας των κινησεων λεει οτι αν δυο κινησεις ειναι μεταξυ τους ανεξαρτητες,εχοντας βεβαιως πρωτα οριστει τι σημαινει αυτο και το εχουμε καταλαβει τι σημαινει αυτο,η εφαρμογη διαδοχικα αυτων των κινησεων,και η αντιμεταθεση μεταξυ τους,η εφαρμογη τους δηλαδη με διαφορετικη σειρα,οδηγει στο ιδιο αποτελεσμα. Αυτο φυσικα ειναι θεωρημα.Αρα για να εφαρμοσουμε το θεωρημα αυτο,πρεπει να δουμε αν ικανοποιουνται οι συνθηκες κατω απο τις οποιες ισχυει. Αν ειχε παρουσιαστει το θεωρημα αυτο στην μαθητρια με τον σωστο τροπο απο την αρχη τοτε αυτη δεν θα εκανε αυτη την λανθασμενη εφαρμογη. Η συνταγη που λεει “Κλείσε το βαρυτικό πεδίο και άσε το σώμα να κινηθεί για χρόνο t. “ δημιουργει δυο κινησεις οι οποιες δεν ικανοποιουν τις συνθηκες του θεωρηματος.Γραφεις Γιαννη:Οι συνθηκες του θεωρηματος ειναι
“Η Vx δεν εξαρτάται από το y και η Vy δεν εξαρτάται από το x.”Εδω οι αξονες x,y ειναι ο εφαπτομενικος και ο πολικος,δεν εχουν καμια σχεση με τα γνωστα μας x,y.H ταχυτητα στον πολικο αξονα δεν μπορει να μην εξαρταται απο την θεση στον εφαπτομενικο διοτι επηρεαζεται ο προσανατολισμος του πολικου αξονα.Αρα το θεωρημα δεν ισχυει για αυτες τις κινησεις σε αυτους τους αξονες.Για αυτο λεω οτι πρεπει να προηγουνται σαφεις διατυπωσεις ορισμων και θεωρηματων.
Σε αυτα θα εδινα εμφαση αν εγραφα για την αρχη της ανεξαρτησιας των κινησεων.Αλλοιως προσπαθει ο μαθητης να βγαλει ακρη απο τα συμφραζομενα. Αν γνωριζουμε οτι τα τρια υψη τριγωνου συντρεχουν δεν θα πουμε οτι τα δυο υψη και μια διαμεσος πρεπει να συντρεχουν. -
Για τον κύριο Κυριακόπουλο.
Η πρώτη περίπτωση που γράφετε καταλήγει σε ό,τι έγραψα εγώ, επειδή η διαφορική εξίσωση κίνησης είναι διαχωρίσιμη και άρα αντιστοιχεί σε 2 ανεξάρτητες διαφορικές εξισώσεις. Η δεύτερη περίπτωση δεν οδηγεί σε ανεξαρτησία των κινήσεων. -
Κωνσταντίνε αντιλαμβάνομαι την αρχή της ανεξαρτησίας των κινήσεων ως:
-Η μετατόπιση ενός σώματος ως προς παρατηρητή Α είναι το διανυσματικό άθροισμα της μετατόπισης του σώματος ως προς παρατηρητή Β και της μετατόπισης του Β ως προς τον Α.Καταλαβαίνω από τον Ανδρέα ότι η λέξη “ανεξαρτησίας” έχει ιστορική προέλευση.
Το θέμα είναι πότε επιτυγχάνει η συνταγή και όχι η καθολικής ισχύος αρχή.
Η μαθήτρια του Ανδρέα κάνει ένα λάθος που έχουμε κάνει και εμείς στο παρελθόν διότι και δεν τα ξέρουμε όλα και συχνά ακολουθούμε συνταγές μηχανικά.
Αυτά που είπες για τις πολικές συντεταγμένες θα τα σκεφτώ. -
Συμφωνώ κύριε Βάρβογλη.
Η περίπτωση Vx=f1(x,y,t) και Vy=f2(x,y,t).δεν οδηγεί σε ανεξαρτησία κινήσεων.
Αναφέρω παραδείγματα στην ανάρτηση (λ.χ. κυκλική κίνηση, αερόστατο).
Η συνταγή τότε αποτυγχάνει.
Η αρχή ουδέποτε αποτυγχάνει. -
Πως αντιλαμβανόμαστε το “κάνει δύο κινήσεις” ;
https://i.ibb.co/X6jZtS1/image.png
https://i.ibb.co/wFzsN8Rc/image.png
https://i.ibb.co/sr2Gknx/image.png -
Θα πρέπει να είμαστε προσεκτικοί και να βεβαιωνόμαστε ότι οι παρατηρητές είναι αδρανειακοί. Όταν ένας παρατηρητής εκτελεί κυκλική ή κυκλοειδή κίνηση, επιταχύνεται.
-
Καλησπέρα κύριε Βάρβογλη.
Η έκφραση “αδρανειακός παρατηρητής” δεν έχει κανένα νόημα στην Κινηματική.
Έχει νόημα μόνο στη Δυναμική διότι αν δεν είναι αδρανειακός παρατηρητής και θέλουμε υπολογισμούς πρέπει να συμπεριλάβουμε κάποιες από τις αδρανειακές δυνάμεις.Πιστεύω πως καταλάβατε ότι τα προηγούμενα δεν είναι σχήματα.
Δεν είναι κάτι που έφτιαξα εγώ και απηχεί την άποψή μου (που μπορεί να είναι και λανθασμένη).
Είναι προσομοιώσεις καλής ακρίβειας,
Όντως π.χ το κοριτσάκι βλέπει την ευθύγραμμη κίνηση αυτήν:
https://i.ibb.co/0ptJBs0P/image.pngΌχι επειδή το λέω εγώ. Ο υπολογιστής σχεδίασε την τροχιά κάνοντας 200 υπολογισμούς το δευτερόλεπτο χωρίς κάποια οδηγία από μένα.
Φυσικά το κοριτσάκι δεν είναι αδρανειακός παρατηρητής.
Ούτε ο Ανδρέας Κασσέτας που σκέφτηκε την περίπτωση είπε ποτέ ότι είναι. -
Οι μη αδρανειακοί παρατηρητές δεν είναι αναξιόπιστοι όσον αφορά τις τροχιές που βλέπουν.
Για παράδειγμα όταν κάθεστε στην περιστρεφόμενη καρέκλα σας και περιστρέφεστε, βλέπετε ένα κάδρο να εκτελεί κυκλική κίνηση.
Δεν είστε αναξιόπιστος διότι όντως το κάδρο απέχει σταθερή απόσταση από εσάς.
Είστε απολύτως αξιόπιστος για την Κινηματική.Απλώς αν θέλετε να βρείτε τις δυνάμεις που δέχεται το κάδρο να μην ξεχάσετε τη φυγόκεντρο και ίσως τις Euler και Coriolis (αν δεν στρέφεστε με σταθερή γωνιακή ταχύτητα).
-
Κύριε Κυριακόπουλε, τα έχετε λίγο μπερδεμένα. Εσείς γράψατε για δυναμικό:
“Επίσης κύριε Βάρβογλη να γενικεύσω κάτι που γράφετε για το x=f1(t) και y=f2(t).
Θα είχαμε ανεξαρτησία ακόμα και αν Vx=f1(x,t) και Vy=f2(y,t).
Τότε η (γενικώς λανθασμένη) συνταγή επιτυγχάνει.
Η αρχή επιτυγχάνει σε κάθε περίπτωση Vx=f1(x,y,t) και Vy=f2(x,y,t).
Επιτυγχάνει διότι είναι σωστή.”Γι’ αυτό και δεν θα συνεχίσω.
-
Κύριε Βάρβογλη εγώ δεν απευθύνομαι σε συνομιλητές μου λέγοντας:
-Τα έχετε λίγο μπερδεμένα.
Έχω επιλέξει άλλο ύφος επικοινωνίας.Έστω. Ασχολήθηκα με δύο διαφορετικά θέματα. Το ένα ήταν πότε πετυχαίνει η συνταγή (ανεξαρτησία κινήσεων). Το άλλο ήταν το ότι κάθε κίνηση αναλύεται.
Μετά από παραδείγματα ανάλυσης κίνησης μου γράφετε:
Θα πρέπει να είμαστε προσεκτικοί και να βεβαιωνόμαστε ότι οι παρατηρητές είναι αδρανειακοί. Όταν ένας παρατηρητής εκτελεί κυκλική ή κυκλοειδή κίνηση, επιταχύνεται.
Σας απάντησα ότι δεν μας απασχολεί το αν οι παρατηρητές είναι αδρανειακοί ή όχι.
Τούτο διότι κινήσεις αναλύουμε και δεν εξετάζουμε το αν είναι ανεξάρτητες ούτε το ποιες δυνάμεις παρουσιάζονται. -
Καλημέρα Γιάννη. Εξαιρετική μελέτη, στο γνωστό ύφος που μας έχεις συνηθίσει. Με παραδείγματα και τα άκρως απαραίτητα Μαθηματικά. Ξεκαθαρίζει τα όρια της γνωστής αρχής.
Θα ήθελα επίσης να αναφερθώ στον τρόπο του Κου Βάρβογλη.
Προφανώς θεωρεί ότι αν δεν καταλάβει κάποιος τα λεγόμενά του σε δυο σχόλια, δεν μπορεί να χάσει περισσότερο το χρόνο του να εξηγήσει. Δεν έχουμε όλοι το ίδιο επίπεδο γνώσεων, αλλά αυτό οφείλεται στις επιλογές μας. Πολλοί από εμάς επιλέξαμε τη Β/θμια Εκπ/ση, οπότε σταματήσαμε να ασχολούμαστε με διαφορικές εξισώσεις και ανάδελτα. Όμως αν κάποιος με ανώτερες γνώσεις μας εξηγήσει κάτι υπομονετικά – όπως ακριβώς κάνουμε εμείς κάθε μέρα στο Σχολείο – θα το καταλάβουμε.Προσωπικά, από τον Κυριακόπουλο έχω μάθει – εκτός από Φυσική – πως μπορεί κάποιος να συνδιαλέγεται πάντα πολιτισμένα και κυρίως ψύχραιμα και με επιχειρήματα, ακόμα και σε περιπτώσεις που ο συνομιλητής είναι ερειστικός. Ο Γιάννης αν δεν ήταν Φυσικός θα μπορούσε να είναι πρέσβης η κυβερνητικός εκπρόσωπος…
-
Καλημέρα Ανδρέα.
Ευχαριστώ.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 6 μέρες, 21 ώρες
Η απόσταση του πρωτονίου σε μαγνητικό πεδίο.
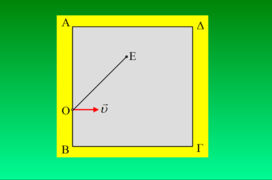 Ένα πρωτόνιο κινούμενο με ταχύτητα υ=2km/s εισέρχεται τη στιγμή t=0, σε ένα ομογενές μαγνητικό πεδίο έντασης Β=10-4Τ, η τομή του οποίου είναι τετράγ […]
Ένα πρωτόνιο κινούμενο με ταχύτητα υ=2km/s εισέρχεται τη στιγμή t=0, σε ένα ομογενές μαγνητικό πεδίο έντασης Β=10-4Τ, η τομή του οποίου είναι τετράγ […]-
Καλημέρα Διονύση.
Όμορφη και ουσιαστική με την έννοια ότι παρέχει βασικά στην ίδια συσκευασία. -
Καλημέρα Διονύση.
Απ’αυτές που μ’αρέσουν !
Ερωτήματα “μαστορικά” δοσμένα !
Να είσαι καλά -
Καλημέρα Διονύση. Ωραίο θέμα, με τον ρυθμό μεταβολής της απόστασης να θέλει την προσοχή του, αφού διαφέρει από το ρυθμό μεταβολής της θέσης…
-
Γεια σας συνάδελφοι.
Γιάννη, Παντελή και Αποστόλη σας ευχαριστώ για το σχολιασμό.
Αποστόλη και γω αυτό το έβαλα σαν κερασάκι 🙂 ξέροντας ότι θα δυσκολέψει… -
Καλησπέρα Διονύση. Ωραία άσκηση, με ιδιαίτερη έμφαση στην ορμή και το ρυθμό της.
Το ερώτημα Iv πήγα να το απαντήσω με παραμετρικές εξισώσεις κύκλου και πήγε πολύ μακριά η βαλίτσα. Πανέξυπνη ιδέα η ανάλυση της ταχύτητας. -
Καλό απόγευμα Ανδρέα.
Σε ευχαριστώ για το σχολιασμό.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα
Ένα πρόβλημα από το βιβλίο των Δεσμών.
 Στο βιβλίο των Δεσμών βρίσκουμε το πρόβλημα 20: Ένα αερόστατο ανεβαίνει από την επιφάνεια της γης με σταθερή κατακόρυφη ταχύτητα υο. Ταυτόχρ […]
Στο βιβλίο των Δεσμών βρίσκουμε το πρόβλημα 20: Ένα αερόστατο ανεβαίνει από την επιφάνεια της γης με σταθερή κατακόρυφη ταχύτητα υο. Ταυτόχρ […]-
Καλησπερα Γιαννη. Δεν ειδα ακομα τι εχεις γραψει στις λυσεις αλλα οι συνθηκες που δινεις ειναι ιδιες με της οριζοντιας βολής αφου στην γνωστη μας οριζοντια βολη με το παραδοσιακο setting στους αξονες,υx=υ0 και υy=gt=(g/υ0)x=Κx οποτε αν αλλαξουμε το ρολο των x,y εχουμε υy=υ0 και υx =Ky που ειναι ακριβως αυτο που δινεις.Η τροχια ειναι παραβολικη.
-
Καλησπέρα Κωνσταντίνε.
Η άσκηση δεν είναι δύσκολη.
Ούτε το να βρούμε ποια λύση είναι σωστή είναι δύσκολο.
Δυσκολότερο είναι το “γιατί;”
Γιατί οι δύο λύσεις βγάζουν τα ίδια στην περίπτωση μιας βολής αλλά εδώ όχι.
Γιατί στο παράδειγμα με το ποτάμι δουλεύουν και οι δύο;
https://i.ibb.co/x8DkmWYL/32.pngΜπορούμε να βρούμε μια βοηθητική συνταγή που να μας λέει πότε δουλεύει το:
-Άστο να κάνει αρχικά την πρώτη κίνηση και στη συνέχεια τη δεύτερη. -
Θυμαμαι που ειχαμε συζητησει πιο παλια κατι σχετικο για τον Ανδρεα και την ερωτηση της μαθητριας.
-
Βεβαίως έχει σχέση.
Στον Ανδρέα οφείλω το ότι κατάλαβα τι λέει η Αρχή της Ανεξαρτησίας των Κινήσεων.
Το καίριο ερώτημά του με έβαλε τότε να κάνω μια προσομοίωση και είδα τι συμβαίνει σε ένα κινούμενο σχέδιο που προέκυψε.
Η συζήτηση όμως είναι παλιά και δεν είναι άσκοπο να ξαναθυμηθούμε κάποια πράγματα. -
Θα προσπαθήσω να φτιάξω μία προσομοίωση για το παρόν θέμα.
Αύριο όμως. -
Γεια σας παιδιά. Μια γρήγορη σκέψη: οι δύο κινήσεις δεν είναι ανεξάρτητες, διότι η υχ εξαρτάται από την κίνηση στον κατακόρυφο άξονα.
-
Συμφωνώ Αποστόλη.
Παλιότερο σχετικό: -
Το προηγούμενο παραείναι γενικό, παραείναι μαθηματικό και περιπλέκει τη Δυναμική.
Σκέφτομαι κάτι καλύτερο, απλούστερο και ενταγμένο αποκλειστικά στην Κινηματική, όπως άλλωστε και το παρόν θέμα που δεν εμπλέκει δυνάμεις. -
Καλημέρα Γιάννη, καλημέρα σε όλους.
Μια υπενθύμιση:
Σύνθετη κίνηση – Αρχή της ανεξαρτησίας. Και είπεν ο κύριος. -
Καλημέρα Διονύση.
Μία από τις προσφορές του Ανδρέα. -
Μία προσομοίωση:
Αερόστατο.Πατώντας “Ακίνητος” ή “ιπτάμενος” βλέπετε ότι βλέπει κάθε παρατηρητής.
(Δουλεύει σε υψηλή ανάλυση) -
Αν δεν έχετε το Interactive physics:
https://i.ibb.co/DfHCc5kR/image.pngΗ θέαση του ακίνητου παρατηρητή.
-
Και η θέαση του ιπτάμενου:
https://i.ibb.co/3y7ZC640/image.pngΒλέπει επιταχυνόμενη κίνηση με μηδενική αρχική ταχύτητα.
-
Αν εφαρμόσουμε λανθασμένα την αρχή της ανεξαρτησίας των κινήσεων.
Το βάζουμε να κάνει την πρώτη κίνηση και να ανέβει σε κάποιο ύψος:
https://i.ibb.co/whCK5DVG/77.png
Μαζί του ανεβαίνει και ο παρατηρητής.Εκεί αποκτά κάποια ταχύτητα και του λέμε να κινηθεί για ίδιο χρόνο με αυτή την ταχύτητα.
Ο παρατηρητής το βλέπει να κάνει ομαλή κίνηση και όχι ομαλά επιταχυνόμενη!Αυτό δεν γίνεται διότι ο παρατηρητής μας πρέπει να βλέπει επιταχυνόμενη κίνηση.
Αυτά δεν συμβαίνουν στην περίπτωση αυτήν:
https://i.ibb.co/x8DkmWYL/32.png -
Γιάννη και Διονύση ευχαριστώ για το σύνολο
των σημαντικών εξορύξεων! -
Καλημέρα Παντελή.
Πέρασαν χρόνια και πολλοί φίλοι μπορεί να μην τα έχουν δει. -
Καλημέρα σε όλους. Όταν διάβασα για πρώτη φορά τα κείμενα του Ανδρέα, κατάλαβα ότι δεν είχα αντιληφθεί την αρχή ανεξαρτησίας και ότι σε κάποιες περιπτώσεις απλά τύχαινε να προκύπτει το σωστό αποτέλεσμα. Οι παραπομπές του Γιάννη και του Διονύση αξίζει να μελετηθούν από συναδέλφους. Γιάννη η προσομοίωση είναι διαφωτιστικότατη.
-
Σε ποιες περιπτώσεις πιάνει η συνταγή:
-Άσε να ανέβει για χρόνο t, ακινητοποίησέ το και βάλτο να κινηθεί οριζόντια για χρόνο t ;
Ένα απόσπασμα από κάτι που γράφω ακόμα:
https://i.ibb.co/ZzLRyc50/88.png -
Γειά σου Γιάννη . Γειά χαρά σε όλους. Το λάθος βρίσκεται στην 1η λύση. Η σχέση χ=υx t δεν ισχύει γιατί η ταχύτητα υx δεν παραμένει σταθερή στο χρόνο .Είναι υx=K υ0 t . Αν βάζαμε τη μέση τιμή της υx σε αυτό το χρονικό διάστημα θα οδηγούμασταν στο ίδιο αποτέλεσμα με τον άλλο τρόπο. Αυτό το λάθος δεν έχει να κάνει με την ισχύ ή όχι της αρχής ανεξαρτησίας των κινήσεων αλλά με το ότι θεωρούμε σταθερή την ταχύτητα υx ενώ δεν είναι! Η αρχή ανεξαρτησίας των κινήσεων δεν ισχύει εδώ . Ο λόγος που δεν ισχύει είναι ότι οι δύο κινήσεις ,στον άξονα x αφενός και στο y αφετέρου, δεν είναι ανεξάρτητες. Αυτό οφείλεται στο ότι το x εξαρτάται από το y. Δεν είναι θέμα σωστής ή λανθασμένης εφαρμογής της εν λόγω αρχής. Η σχέση όμως r=xi + yj και οι αντίστοιχες για την ταχύτητα και την επιτάχυνση ισχύουν σε κάθε περίπτωση. Είτε οι κινήσεις είναι ανεξάρτητες είτε όχι. Με άλλα λόγια η τελευταία σχέση ισχύει είτε ισχύει η αρχή της ανεξαρτησίας των κινήσεων είτε όχι.
-
Ξέφυγε από την προσοχή μου το ότι η αρχή ανεξαρτησίας των κινήσεων ισχύει! Τα x και y είναι συναρτήσεις του χρόνου και μόνο! Άλλωστε στον άξονα x ενεργεί σταθερή δύναμη. Όπως το βάρος στην οριζόντια βολή στον άξονα y.
-
Καλησπέρα Γιώργο.
Καλά τα λες στο πρώτο σχόλιο.
Επιφυλάσσομαι στο δεύτερο.
Υπάρχουν δύο προτάσεις.
Η πρώτη:
-Η μετατόπιση ενός σώματος ως προς παρατηρητή Α είναι το διανυσματικό άθροισμα της μετατόπισης του σώματος ως προς παρατηρητή Β και της μετατόπισης του Β ως προς τον Α.Η δεύτερη:
-Κλείσε το πεδίο και άσε το σώμα να κινηθεί για χρόνο t. Εκεί που θα πάει ακινητοποίησέ το και άνοιξε το διακόπτη του πεδίου. Άσε το σώμα να κινηθεί για χρόνο t και έχεις βρει την τελική θέση.Ποια από της δυο είναι η καλουμένη “Αρχή της ανεξαρτησίας των κίνήσεων”;
Με αφορμή το παρόν πρόβλημα η ανάρτηση:
Η ισχύς της αρχής της ανεξαρτησίας των κινήσεων. -
Γιάννη από όσα αντιλαμβάνομαι η πρώτη διατύπωσή σου είναι κάτι γενικότερο της αρχής ανεξαρτησίας των κινήσεων. Η δεύτερη ισχύει όταν οι κινήσεις είναι ανεξάρτητες. Στο ομογενές βαρυτικό πεδίο είναι ανεξάρτητες και στο μη ομογενές- πλανητάκος – δεν είναι. Αυτό εύκολα διαπιστώνεται στο ομογενές . Στο ανομοιογενές η αρχική διαπίστωσή μου προέκυψε από συγκεκριμένο παράδειγμα. Μια εξήγηση στη περίπτωση της οριζόντιας βολής είναι ότι στον άξονα x της αρχικής ταχύτητας στο ομογενές η βαρυτική δύναμη δεν δίνει συνιστώσα ενώ στο ανομοιογενές δίνει. Και η συνιστώσα αυτή στη περίπτωση του ανομοιογενούς εξαρτάται από το y. Συνεπώς θα εξαρτάται από το y και το x όπως προκύπτει από τη λύση της διαφορικής εξίσωσης στον άξονα x. Στην περίπτωση του αεροστάτου εύκολα διαπιστώνεται ότι στον οριζόντιο άξονα x ενεργεί σταθερή δύναμη συνεπώς είναι η περίπτωση της οριζόντιας βολής με τις προφανείς επουσιώδεις διαφοροποιήσεις. Αν βρω χρόνο θα αναφερθώ αναλυτικότερα.
-
Γιώργο στο πρώτο μου σχόλιο θα συμφωνήσω μαζί σου επί της ουσίας, ότι δηλαδή η πρώτη πρόταση είναι γενικότερη.
Στο δεύτερο θα εντοπίσω ένα λάθος που κάνω συστηματικά.
Η πρώτη πρόταση λέει :
-Η μετατόπιση ενός σώματος ως προς παρατηρητή Α είναι το διανυσματικό άθροισμα της μετατόπισης του σώματος ως προς παρατηρητή Β και της μετατόπισης του Β ως προς τον Α.
Οδηγεί στην:
Θέλεις να βρεις τη θέση τη στιγμή t ενός σημείου (υλικού ή όχι υλικού) που κάνει δύο κινήσεις ταυτόχρονα;
Βάλε το να εκτελέσει την πρώτη κίνηση για χρόνο t. Από το σημείο Β που θα πάει βάλε το να εκτελέσει τη δεύτερη κίνηση. Θα βρεθεί στο σημείο Γ. Αυτή είναι η ζητούμενη θέση.
Το τι σημαίνει όμως «Η πρώτη κίνηση» και «Η δεύτερη κίνηση» στο επόμενο σχόλιο με το λάθος μου. -
Ποιο είναι το λάθος που κάνω συστηματικά;
Θεωρώ ότι όλοι έχουν διαβάσει και έχουν ενστερνιστεί όσα συζητούσαμε το 2010.
Και είπεν ο κύριος.
Κάτι φυσικά εντελώς παράλογο μια και ουδείς μπορεί να απαιτήσει να έχουν όλοι διαβάσει και ενστερνιστεί μια συζήτηση που αυτός συμμετείχε.
Την εποχή εκείνη όλοι ταυτίζαμε την «Αρχή της ανεξαρτησίας των κινήσεων» με τη δεύτερη πρόταση:
-Κλείσε το πεδίο και άσε το σώμα να κινηθεί για χρόνο t. Εκεί που θα πάει ακινητοποίησέ το και άνοιξε το διακόπτη του πεδίου. Άσε το σώμα να κινηθεί για χρόνο t και έχεις βρει την τελική θέση.
Καταλήγαμε στην προϋπόθεση της ανεξαρτησίας των κινήσεων και αμφισβητούσαμε την καθολικότητα της ισχύος της, ούτως ειπείν, «αρχής».
Ο Ανδρέας Κασσέτας παρενέβη με το περίφημο ερώτημα της μαθήτριας και κάποιοι καταλάβαμε τι σημαίνει το «Κάνει δύο κινήσεις».
Κινείται πάνω σε κινούμενο όχημα. Ο παρατηρητής Β ουσιαστικά κάνει τη μία κίνηση και το σώμα την άλλη ως προς τον Β.
Κινηματική (Γεωμετρία μετά χρόνου) και όχι Δυναμική.
Δύο κινήσεις που δεν ταυτίζονται σε κάθε περίπτωση με συντεταγμένες. Που μπορεί να είναι από εξόχως απλές ως εξαιρετικά πολύπλοκες. Λόγου χάριν μια κυκλική κίνηση αναλύεται σε μια ευθύγραμμη ομαλή και μία με τροχιά κυκλοειδές! (Η περίπτωση της μαθήτριας).
Είχα δηλώσει τότε ότι κατάλαβα. Χρωστώ πολλά στον Ανδρέα και αυτό είναι ένα από αυτά.
Εν τούτοις βλέπω και σήμερα διαφωνίες και επιφυλάξεις. Βλέπω το «κάνει δύο κινήσεις» να ταυτίζεται με το «έχει δύο συντεταγμένες», κάτι που δεν με ενοχλεί βέβαια αλλά δεν είναι η μοναδική περίπτωση. -
Γιάννη μπήκα πολύ αργά στο υλικό και έχω χάσει αυτές τις ωραίες συζητήσεις. Θα ήθελα όμως να συμμετέχω όπως είμαι τώρα .Του τώρα που ξεκινάει από την σχετική δήλωση – υπόσχεση μου. Με σεβασμό στον κάθε συνομιλητή στο κοινό πρωταρχικό σκοπό της βαθύτερης κατανόησης της φυσικής. Το “γηράσκω αεί διδασκόμενος” να ισχύει σε όλες του τις εκφάνσεις…
-
Αυτό είναι το λάθος μου Γιώργο.
Λάθος που κάνουν και άλλοι από τους παλιούς του υλικονέτ (με εξαίρεση τον Διονύση).
Πρέπει να λέμε καθαρά τι εννοούμε λέγοντας “Κάνει δύο κινήσεις” ή οτιδήποτε άλλο. -
Θα πω Γιάννη το προφανές . Κανείς μας δεν έχει το αλάθητο. Και χρειάζεται γενναιότητα για να αναγνωρίσει κανείς το λάθος του! Και εσύ την έχεις και το κάνεις με ευθύτητα και παρρησία! Δεν το κάνουν όλοι…Όταν κάποιος αναλαμβάνει δημόσια την ευθύνη να ασχοληθεί με διάφορα ιδιαίτερα απαιτητικά θέματα της επιστήμης μας, ελλοχεύει πάντα το ενδεχόμενο του λάθους! Το έκανα κι εγώ και μεσολάβησε χρόνος για να το κατανοήσω. Όλους τους προσωπικούς εγωισμούς τους υπερβαίνουμε ευκολότερα όταν σκοπός μας είναι να κατανοήσουμε βαθύτερα την επιστήμη μας. Δηλαδή το πως λειτουργεί η φύση.
-
Καλημέρα Γιώργο.
Σωστά.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα
Ένα ταξίδι στο ποτάμι.
 Έχουμε ένα ποτάμι με στρωτή ροή. Έχει παντού το ίδιο βάθος και οι όχθες του είναι ευθύγραμμες. Στενεύει όπως φαίνεται στο κάτω σχήμα έτσι ώστε […]
Έχουμε ένα ποτάμι με στρωτή ροή. Έχει παντού το ίδιο βάθος και οι όχθες του είναι ευθύγραμμες. Στενεύει όπως φαίνεται στο κάτω σχήμα έτσι ώστε […]-
Γειά σου Γιάννη. Δεν αξιολόγησα ότι το στένωμα είναι γραμμική συνάρτηση του αρχικού εμβαδού, θεωρώντας ακαριαία μεταβολή στο μέσο της ΑΒ στο μισό.Έτσι ο συνολικός χρόνος προέκυψε 10,5 min
-
Γεια σου Θύμιο.
Αν κατάλαβα καλά είπες ότι η ταχύτητα γίνεται στο δεύτερο μισό διπλάσια και ο χρόνος μισός (3,5 λεπτά). Συνολικά 10,5 λεπτά. -
Γεια σου Θοδωρή.
Πηγές Αχέροντα:
https://i.ibb.co/fVWj19B9/22.pngΔεν βλέπεις κράνη μια και είναι εύκολη διαδρομή.
-
Γεια σου Γιάννη, Εύηνος 2003, γέφυρα Μπανιά
-
Γιάννη, καλησπέρα (και καλή χρονιά αν δεν τα είπαμε).
Ευφυείς οι λύσεις σου. Ειδικά στην πρώτη αποφεύγεις εντέχνως το ολοκλήρωμα με υπολογίσιμο εμβαδόν. Και με τον τυφλοσούρτη (ολοκλήρωμα για το χρόνο μέχρι τη μέση και σε ολόκληρο και με σύγκριση μεταξύ τους) καταλήγουμε στο ίδιο αποτέλεσμα. -
Καλησπέρα Ντίνο.
Ευχαριστώ. -
Καλησπέρα Γιάννη. Πολύ όμορφη!
Ειπα να αρχίσω με τυχαία θεση του Μ και τυχαιο λογο διατομών και βγηκε το παρακάτω. Στην 3η σελιδα δινεται η λυση για τις τιμές που εχεις.https://i.ibb.co/7JXpp9r0/SCAN-ian-30.png -
Ευχαριστώ Γιώργο.
Ωραία λύση!
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 1 μέρα
Η τελική απόσταση των δύο αγωγών.
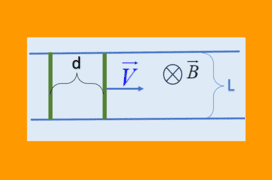 Το επίπεδο είναι οριζόντιο. Οι μπλε αγωγοί δεν έχουν αντίσταση και οι πράσινοι έχουν μαζί αντίσταση R. Κάθε πράσινος έχει μάζα m και μήκος L […]
Το επίπεδο είναι οριζόντιο. Οι μπλε αγωγοί δεν έχουν αντίσταση και οι πράσινοι έχουν μαζί αντίσταση R. Κάθε πράσινος έχει μάζα m και μήκος L […]-
Γεια σου Γιάννη, πολύ όμορφη άσκηση.
Μια παρόμοιας λογικής αλλά με νούμερα εδώ . -
Ευχαριστώ Παύλο. Όμορφη η άσκησή σου
-
Ευχαριστώ Γιάννη.
-
Καλημερα σε ολους .Και για να μην ξεχναμε οτι ειμαστε και λιγο μυστήριοι,η αποσταση των δυο αγωγων δεν γινεται ποτε μέγιστη. Η αποσταση που εχουμε βρει ο Γιάννης,ο Γιώργος και εγώ, ειναι η οριακη αποσταση,η οποια δεν ανηκει στο συνολο των αποστασεων. Ειναι το ελαχιστο ανω φραγμα αυτου του συνολου και οι μαθηματικοι το ονομαζουν Supremum.
-
Καλημέρα και από εδώ παιδιά.
Ωραίες λύσεις βάλατε. -
Καλημερα Γιαννη. Ξενυχταω και σου στελνω λυσεις Zulu. 🙂 Στο κυριως ερωτημα που λεει και ο τιτλος γιατι τα αλλα ειναι τελειως απλα. Πολυ ωραια ασκηση.Κατι παρομοιο ειχε ρωτησει και ο Παρμενίων και τοτε ηταν και η πρωτη φορα που μιλησαμε μαζι στο Υλικο και ειχαμε ωραια συζητηση.
Μια άσκηση και ένας προβληματισμός
Περνάνε τα χρόνια…
Τοτε υπηρχαν διαφωνιες για το αν μια τετοια ασκηση ειναι νομιμη ή οχι.
https://i.ibb.co/gb5pphPQ/5654.jpg -
Kαλημέρα παιδιά.
Ανεβάζω κάποιες επικίνδυνες σκέψεις που κάνει ο αρχικά ακινητος αγωγός για τον πρόσθιο αλλά μην τον κράξετε. -
Καλημέρα σε όλους. Ωραίες και οι δύο Γιάννη. Παλιά κάναμε και τέτοια, τώρα η οδηγία είναι σαφής
-
Καλημέρα Αποστόλη.
Ευχαριστώ.
Οπότε έχει θέση μόνο στο φόρουμ.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 1 μέρα
Ένα πλαίσιο βάλλεται.
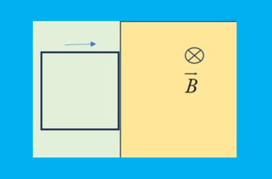 Έχουμε ένα τετράγωνο κλειστό αγώγιμο πλαίσιο με σχήμα τετραγώνου πλευράς L. Έχει ολική αντίσταση R και μάζα m. Ποια η ελάχιστη ταχύτητα με την ο […]
Έχουμε ένα τετράγωνο κλειστό αγώγιμο πλαίσιο με σχήμα τετραγώνου πλευράς L. Έχει ολική αντίσταση R και μάζα m. Ποια η ελάχιστη ταχύτητα με την ο […]-
Καλησπέρα Γιάννη. Πολύ καλή. Η άθροιση βέβαια δεν είναι και το καλύτερο για τους μαθητές Υγείας, αλλά είναι στην ύλη τους-π.χ. Ampere.
Θα μπορούσαμε να πάρουμε και το ΘΩΟ
Ω = Σ(Fdt) (ολοκλήρωμα) = Β^2L^2/RΣυdt = Β^2L^2/RΣdx = Β^2L^3/R
0 – mυ0 = Β^2L^3/R
υ0 = Β^2L^3/mR -
Καλησπέρα Ανδρέα.
Ευχαριστώ.
Ναι δεν είναι εύκολη. -
Καλημέρα Γιάννη.
Βλέπω να μπήκες πολύ δυναμικά στην επαγωγή.
Με τον υπολογισμό του ολοκληρώματος (έστω και πλαγίως…) δεν ξέρω τι γίνεται… -
Μια επι πλέον ερώτηση αφού ο Γιάννης έχει οργώσει το έδαφος και δεν απαιτεί μαθηματικούς υπολογισμούς.
Αν το πλαίσιο που έχει διάσταση L βληθεί με ταχύτητα 2V0 και το πεδίο έχει ίδια μήκος L θα τα καταφέρει να εξέλθει? -
Καλημέρα παιδιά.
-
Καλημέρα
Διονύση έχω ανακαλύψει(φσσσ) τρόπο για να αποφεύγω τα αθροίσματα που τρομοκρατούν.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 1 μέρα
Μια ισορροπία σε κεκλιμένο επίπεδο
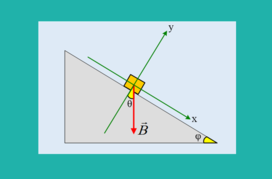 Ένα σώμα βάρους 50Ν ισορροπεί σε κεκλιμένο επίπεδο κλίσεως φ, όπου ημφ=0,6 και συνφ=0,8. i) Να σχεδιάσετε την δύναμη Α που το επίπεδο α […]
Ένα σώμα βάρους 50Ν ισορροπεί σε κεκλιμένο επίπεδο κλίσεως φ, όπου ημφ=0,6 και συνφ=0,8. i) Να σχεδιάσετε την δύναμη Α που το επίπεδο α […]-
Καλημέρα Διονύση.
Καλά κάνεις και βάζεις το:
Να αποδείξετε ότι η γωνία που σχηματίζει το βάρος με τον άξονα y, είναι ίση με την κλίση του επιπέδου (θ=φ).
Οι μαθητές κάνουν μηχανικά τη μεταφορά (ακολουθούν οδηγίες) και σε άλλες περιπτώσεις αγνοούν το ότι δύο οξείες με κάθετες πλευρές είναι ίσες. Η απόδειξη που παραθέτεις θα βοηθήσει σε άλλες ασκήσεις και όχι μόνο Στατικής. -
Καλημέρα παιδιά. Μου έχει συμβεί να ρωτήσω μαθητές, για ποιο λόγο η γωνία του κεκλιμένου μεταφέρεται μεταξύ Β και Βy και να πάρω απάντηση: γιατί μας έχουν πει ότι πάντα εκεί μεταφέρεται…
-
Καλό απόγευμα Γιάννη και Αποστόλη, σας ευχαριστώ για το σχολιασμό.
Είπα να το πάμε σιγά – σιγά από τα βασικά…
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 2 μέρες
Πότε άρχισε να χιονίζει;
 Μια μέρα αρχίζει να πέφτει πολύ χιόνι με σταθερό ρυθμό. Ένα εκχιονιστικό ξεκινάει να το μαζεύει το μεσημέρι. Διανύει την πρώτη ώρα 2 km και τη δεύτερ […]
Μια μέρα αρχίζει να πέφτει πολύ χιόνι με σταθερό ρυθμό. Ένα εκχιονιστικό ξεκινάει να το μαζεύει το μεσημέρι. Διανύει την πρώτη ώρα 2 km και τη δεύτερ […]-
Καλημέρα Γιάννη, Δυο ώρες πριν; Δηλαδή στις 10;
-
Καλό μεσημέρι Γιάννη.θεωρώντας τις ώρες διαδοχικούς όρους γεωμετρικής προόδου προκύπτει μισή ώρα πριν.
-
Μια πρωτη σκέψη:
Την 1η ωρα μαζεύει : m1= mαρχ + m
mαρχ : η αρχικη ποστητα χιονού που υπάρχει το μεσημέρι
m : η ποσότητα που πεφτει την 1η ώρα
Την 2η ώρα μαζεύει: m2= mαρχ/2 +2m
Αν μαζεύει με τον ίδιο ρυθμό m1=m2
αρα mαρχ +m= mαρχ/2+2m => mαρχ = 2m
Αρα είχε αρχικό χιόνι για 2 ώρες. -
Καλημέρα Γιώργο.
Όχι
Δυστυχώς το πρόβλημα θέλει μια απλή ΔΕ . Έχει λογαρίθμους στην πορεία. -
Παρ’όλο που λες ότι λυνεται αλλιώς ,διορθώνω την αρχική λύση (ας είναι και αυτη λάθος):
Την 1η ωρα μαζεύει : m1= mαρχ+ m
mαρχ : η αρχικη ποστητα χιονού που υπάρχει το μεσημέρι
m : η ποσότητα που πεφτει την 1η ώρα
Την 2η ώρα μαζεύει: m2= mαρχ/2 +3m/2
Αν μαζεύει με τον ίδιο ρυθμό m1=m2
αρα mαρχ +m= mαρχ/2+3m/2 => mαρχ = m
Αρα είχε αρχικό χιόνι για 1 ώρα. -
Θύμιο είναι περίπου 37 λεπτά.
-
Ισως πρέπει να χρησιμοποιήσουμε τους ρυθμούς πτωσης και μαζέματος χιονιου.
Πιθανόν δεν διανύει το μισό διαστημα την 2η ώρα (δεν έχει σταθερή ταχύτητα)
Θα το δω αργότερα. -
Γεια σου Γιαννη. Ετσι οπως την διαβαζω δεν την βλεπω να λυνεται αν δεν βαλω και δικα μου δεδομενα στο προβλημα.
-
Λύνεται Κωνσταντίνε.
Έχω γράψει μια λύση. Θα τη στείλω μαζί με το βίντεο.
Αυτό που γράφω τώρα είναι η εμπλοκή της χρυσής τομής και του αριθμού φ στο πρόβλημα. -
Η λύση έχει μπει μετά την εκφώνηση.
Το βίντεο που δίνει το πρόβλημα:Δεν ξέρω αν υπάρχει γεωμετρική λύση που δεν βλέπω.
-
Καλημερα Γιαννη. Στο βιντεο που αναφερεσαι εχει μια επιπλεον υποθεση την οποια ανομαζει modeling assumpsion.Oτι η ταχυτητα της μηχανης ειναι αντιστροφως αναλογη του υψους χιονιου. Αν δεν υποθεσεις κατι τετοιο τοτε η ασκηση δεν λυνεται.
Στα δεδομενα που δινεις κανείς καταλαβαινει οτι απλως η ταχυτητα μειωνεται αφου την πρώτη ώρα διανυει 2 km και τη δεύτερη 1 km.Δεν ξερουμε ομως τιποτα για τον ρυθμο μειωσης.Αν μας ελεγε οτι ο ρυθμος με τον οποιο η μηχανη μαζευει το χιονι ειναι σταθερος,που ειναι ισοδυναμη υποθεση, τοτε θα ξεραμε τι να κανουμε.Βεβαια δεν διαφωνω οτι αυτη ειναι μια λογικη υποθεση που καποιος μαλλον πρεπει να την κανει. Εγω παντως δεν την εκανα. 🙂 -
Καλημέρα Κωνσταντίνε.
Γράφω στη λύση:
https://i.ibb.co/d4XS2mJZ/Screenshot-1.pngΔηλαδή ας πούμε ότι μαζεύω 2 κέρματα το δευτερόλεπτο και προχωρώ σε μια γραμμή που έχουν τοποθετηθεί κέρματα. Η ταχύτητά μου είναι αντιστρόφως ανάλογη της πυκνότητας των κερμάτων.
-
Γιαννη δεν με καταλαβες.Το οτι το εκχιονιστικο μαζευει χιονι με σταθερο ρυθμο,ειναι κατι που το γραφεις στην λυση αλλα ειναι δικη σου υποθεση. Δεν το γραφει στην εκφωνηση. Θα επρεπε να το γραφει κατα την γνωμη μου. Δεν προκυπτει απο καπου.
-
Κωνσταντίνε είναι μια υπόθεση που πρέπει να κάνουμε στο παρόν θέμα.
Μια αντλία αφαιρεί νερό με κάποιο ρυθμό. Ένα περιστέρι τρώει σποράκια με κάποιο ρυθμό.
Αν ο ρυθμός εκχιονισμού ήταν μεταβλητός τότε η ταχύτητα θα ήταν οποιαδήποτε.
Τώρα βέβαια ένα τεράστιο εκχιονιστικό που θέλει να καθαρίσει ένα δρόμο με χιόνι μερικές παλάμες μπορεί να κινείται με σταθερή ταχύτητα π.χ. 10 km/h όποιο και να είναι το ύψος του χιονιού που συναντά. Τότε ο ρυθμός εκχιονισμού αυξάνεται.
Κράτησα την εκφώνηση όμως ήταν. -
Μου θυμησες ενα ανεκδοτο.
Κυρία : Ενας εργατης που σκαβει με σταθερο ρυθμο,για να σκαψει ενα χωραφι θελει τρεις μερες. Τρεις εργατες αν σκαβουν μαζι,το σκαβουν σε μια μερα. Τo καταλαβατε;
Παιδακια : Ναι Ναι
Κυρία : Μπορει καποι παιδακι να μου πει ενα αλλο παραδειγμα;
Tοτός: Kυρία Κυρία…
Κυρία : Πες Τοτέ
Tοτός: Ενα πλοιο που φευγει για την Αμερική φτανει σε τρεις μερες. Αν φυγουν τρια πλοια μαζι φτανουν σε μια μέρα! -
Γεια σου Γιάννη.
Ξεκίνησα να την κοιτάζω από το video. Μα βάση τους συμβολισμούς του έγραψα περίπου ως προφανή την h(t)=k1(t+b) και εκεί έμεινα. Και νομίζω ότι δεν θα έφτανα ποτέ στην X’(t) h(t)=Κ2 διότι συμφωνώντας με τον Κωνσταντίνο θεωρώ ότι δεν προκύπτει από την εκφώνηση.Έχω την άποψη ότι αν κανείς δώσει την άσκηση με την προσθήκη «το εκχιονιστικό με σταθερό ρυθμό δηλαδή ο όγκος του χιονιού που μαζεύει είναι ανάλογος του χρόνου» την κάνει προσβάσιμη χωρίς αυτή να χάνει το ξάφνιασμα που προκαλεί γενικά
-
Άρη μετάφραση έκανα.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 3 μέρες
Βρείτε το μαγνητικό πεδίο.
 ΟΙ τρεις αγωγοί είναι κάθετοι στο επίπεδο . Διαρρέονται από ρεύματα ίσα με 1 Α. Περνάνε από τα σημεία A, B, Γ. και (ΑΒ)=2cm, (ΑΓ) = 3 […]
ΟΙ τρεις αγωγοί είναι κάθετοι στο επίπεδο . Διαρρέονται από ρεύματα ίσα με 1 Α. Περνάνε από τα σημεία A, B, Γ. και (ΑΒ)=2cm, (ΑΓ) = 3 […]-
Η απάντηση γράφτηκε.
Πρόκειται για άσκηση Φυσικής;; -
Όχι δεν είσαι Καρδινάλιος 🙂
-
Κι εγώ Γιάννη πιστεύω πως μεσογειακός τύπος είσαι όχι όμως “Καρδινάλιος” όπως τούτο
https://i.ibb.co/7Jbnh44D/image.png -
Παντελή δεν ήξερα πως υπάρχει τέτοιο ψάρι.
-
Προφανώς.
Βλέπεις όμως Διονύση ότι οι προσπάθειες εμπλουτισμού των συλλογών ασκήσεων σημειώσεων και βιβλίων. έχουν δημιουργήσει ένα καλό πλήθος τέτοιας λογικής ασκήσεων.
Ο Ηλεκτρομαγνητισμός είναι βολικό πεδίο για τέτοιες κατασκευές.
Έκανες εδώ ακριβώς το αντίθετο. Η Φυσική κυριαρχεί απόλυτα και σε δύο σημεία επικαλείται κάποια γεωμετρικά με το τελευταίο λιγότερο συνηθισμένο από το πρώτο. -
Γεια σας παιδιά. Γιάννη η Φυσική της άσκησης, τώρα που υπάρχει και το τυπολόγιο, περιορίζεται στην εφαρμογή του κανόνα του δεξιού χεριού…
-
Καλησπέρα Γιάννη, Σιγουρα δεν είναι μια όμορφη άσκηση και καθόλου ελκυστική για τους μαθητές μας(στην εποχή μας θα την βλεπαμε ´πιο φυσιολογική¨)’
¨Ομως θα κάνω τον δικηγόρο του διαβόλου.
Αυτη η άσκηση ως προς την Φυσική εξετάζει τις φορές των μαγνητικών πεδίων , εκτος από τα μέτρα τους, την συμμετρία μεταξύ των Β,Γ (που αρκετος λογος γινεται εδω τωρα) και τον τύπο του μετρου της εντασης του μαγνητικού πεδίου/
Αν η εκφωνηση ελεγε μονο ¨βρείτε την φορά του μαγνητικού πεδίου από τα Α,Β,Γ” δεν θα ήταν ασκηση Φυσικής και μάλιστα όχι τοσο κακή; -
Αποστόλη συνταξιοδοτηθείς δεν πρόλαβα το τυπολόγιο.
Έχεις δίκιο. -
Γιώργο ο υπολογισμός της γωνίας είναι ένα ακόμα γεωμετρικό πρόβλημα.
Δεν είναι άσχημες ασκήσεις αλλά ξεφεύγουν από τις προδιαγραφές που πρέπει να έχουν οι ασκήσεις Φυσικής.
Εμείς όντως τις είχαμε συνηθίσει μια και η Γεωμετρία ήταν το πιο βαρύ από τα μαθήματα που δίναμε τότε. -
Παρ’ όλα αυτά επειδή αν η εκφωνηση ελεγε μονο ¨βρείτε την φορά του μαγνητικού πεδίου από τα Α,Β,Γ” και τότε δεν θα ήταν κακή ασκηση Φυσικής ,
έχει ¨αρωμα” Φυσικής. -
Άλλωστε είπα: Να κάνω τον δικηγόρο του διαβόλου……
-
Θα συμφωνήσω με τον Γιώργο, θα μπορούσε να είναι ένα εξαιρετικό, κατά τη γνώμη μου, Θέμα Α το οποίο θα έδινε 4 διαφορετικές εκδοχές για το διάνυσμα Β στο σημείο Μ. Δεν θέλει υπολογισμούς, είναι ανάκληση γνώσης και αξιολογεί στο μέγιστο βαθμό την ικανότητα αντίληψης στη σχεδίαση των διανυσμάτων.
Γιάννη γλυτώνεις το ταξίδι στο Βατικανό, επειδή ζητάς μέτρο του Β και το Απολλώνιο Θεώρημα μόνο εσύ και ο Παντελής το θυμάστε
Ας δώσω λοιπόν και εγώ τον κόκκινο καρδινάλιο -
Τέτοια θέματα με αριθμητικούς υπολογισμούς του μέτρου του διανύσματος σε πιο light εκδοχές όπου το μήκος (ΑΜ) υπολογίζεται normal δεν είναι “γοητευτικά” θέματα φυσικής, σε επίπεδο πανελλαδικών.
Είναι θέματα για “αμερικανάκια” που χρησιμοποιούν άκριτα έτοιμους τύπους και δεν κάνουν αρχικά διερεύνηση αν υπάρχει τέτοιο τρίγωνο….
Οι καλόπιστοι μαθητές οφείλουν να γνωρίζουν να τα διαχειρίζονται από τη Β’ Λυκείου, όταν εκεί πρέπει να τους διδάσκουμε κατά το ΙΕΠ μόνο συγγραμμικά διανύσματα …..
Χωρίς κανένα αριθμητικό δεδομένο με μόνο δεδομένο ότι Ι1=Ι2=Ι3 και σχεδίαση του διανύσματος Β στο Μ, είναι καθαρή φυσική, ιδανική για θέμα Α σε “ρωσάκια” την εποχή της ΕΣΣΔ….
Ο Γιάννης grand master στη χρήση γεωμετρικών ξεχασμένων θεωρημάτων, έστησε κάτι κραυγαλέα αποκρουστικό για φυσική, κάτι βαριά “σταλινικό” … με άρωμα από το Βατικανό…
Ο Γιώργος πρόβαλε μία “αναθεωρητική” άποψη την οποία πρόθυμα υποστήριξα….
Ενδιαφέρον θα είχε και η γνώμη του άλλου Γιώργου, του ψηλού, που “σνομπάρει”…
και κάνει μόνο έρευνα επιστημολογικών χαρακτηριστικών…Καλημέρα παιδιά, σε λίγο θα έχω ρεαλιστικά στοιχεία
-
Καλημέρα παιδιά.
Επειδή ο Γιώργος και ο Θοδωρής βάλθηκαν να χειροτονήσουν το Γιάννη και μάλιστα σε ανώτατο αξίωμα 🙂 να επιχειρηματολογήσω υπέρ του.
Αν δεν ζητούσε την ένταση στο μέσον Μ της ΒΓ και δεν έδινε τις πλευρές του τριγώνου που έδωσε, απλά εστίαζε στην κατεύθυνση του Β ή ακόμη και δίνοντας το μήκος της διαμέσου, ζητούσε το μέτρο του Β, τότε ναι, θα είχαμε ένα Α ή έστω Β θέμα κατάλληλο και για εξετάσεις.
Αλλά τότε δεν θα ήταν το παραπάνω θέμα, αλλά κάτι άλλο! -
Καλημέρα παιδιά.
Φυσικά υπάρχουν πολύ όμορφα θέματα Φυσικής με τρεις αγωγούς.
Αυτό του Διονύση για παράδειγμα.
Δεν ήθελα να κατασκευάσω ένα τέτοιο αλλά να εντοπίσω ότι πολλά θέματα Ηλεκτρομαγνητισμού διολισθαίνουν προς Γεωμετρία. -
Τα ρεαλιστικά στοιχεία που υποσχέθηκα από τμήμα αμιγώς Γθετ
60% των μαθητών σχεδίασαν με ακρίβεια, άνεση και γρήγορα το διάνυσμα της έντασης στο μέσο Μ με μοναδικό δεδομένο πως τα ρεύματα είναι ίσα
15% των μαθητών γνώριζαν το θεώρημα των διαμέσων ώστε να βρουν το μήκος της ΑΜ και στη συνέχεια το μέτρο της έντασης στο Μ
-
Καλημέρα παιδιά.
Θοδωρή χαίρομαι που κάποια παιδιά γνωρίζουν Γεωμετρία και με αιφνιδίασε το ποσοστό (έστω και σε καλό σχολείο).
Ασχολούμαι χομπυστικώς με τη Γεωμετρία αλλά δεν έχω διδάξει Γεωμετρία ποτέ εκτός από τότε που βοηθούσα τους γιους μου σε ασκήσεις. Χρόνια πολλά πριν.
Έτσι δεν έχω ούτε γνώση του τι διδάσκεται σήμερα ούτε τι βαρύτητα έχουν τα θεωρήματα διαμέσων.
Για να βάλεις θέματα πρέπει όχι μόνο να γνωρίζεις το αντικείμενο αλλά να έχεις και την αίσθηση του πόσο θεμελιώδη είναι όσα ζητάς.
Αν δεν την έχεις στήνεις θέματα τύπου PISA.Έτσι βέβαια απέφευγα σε Εξετάσεις τέτοια θέματα βάζοντάς τα μόνο εδώ στο υλικονέτ και δη στο φόρουμ. Για παιγνιώδεις λόγους.
Για παιγνιώδεις λόγους μπορούμε να ανοίξουμε ένα βιβλίο Γεωμετρίας και να μετατρέψουμε σχεδόν κάθε άσκηση σε άσκηση Φυσικής.
Ένα τέτοιο παιγνίδι ήταν:
Κινδυνεύει; Ένα δύσκολο κουίζ.Τη δύναμη σημείου τη διδάχτηκε ο μεγάλος γιός μου αλλά όχι ο “μικρός” μια και τότε είχε εξαιρεθεί από την ύλη. Τον Απολλώνιο κύκλο ουδείς των γιών μου διδάχτηκε, έτσι το παραπάνω θέμα δεν είναι για μαθητές. Το ανάρτησα για παιγνιώδεις λόγους.
Η παρούσα ανάρτηση έχει σατιρική διάθεση. Είχε πρόθεση να σατιρίσει την τάση κατασκευής ασκήσεων με ελάχιστη Φυσική και περισσότερα Μαθηματικά.
Μια τάση που εμφανίζεται κυρίως στον Ηλεκτρομαγνητισμό. Ο Ηλεκτρομαγνητισμός είναι βολικό πεδίο αν θέλεις να ανοίξεις ένα βιβλίο Γεωμετρίας και να μετατρέψεις μια άσκηση σε άσκηση Φυσικής. Παράγεις έτσι ασκήσεις με άρωμα Φυσικής αλλά όχι ασκήσεις Φυσικής.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 3 μέρες
Τρεις αγωγοί και τα μαγνητικά πεδία τους.
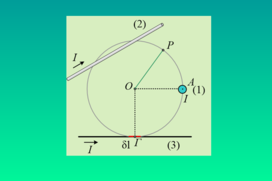 Στο επίπεδο της σελίδας δίνεται ένας κύκλος κέντρου Ο. Στο χώρο έχουμε τρεις ευθύγραμμους αγωγούς (1), (2) και (3), μεγάλου μήκους, οι οποί […]
Στο επίπεδο της σελίδας δίνεται ένας κύκλος κέντρου Ο. Στο χώρο έχουμε τρεις ευθύγραμμους αγωγούς (1), (2) και (3), μεγάλου μήκους, οι οποί […]-
Καλημέρα Διονύση.
Πολύ καλά όλα τα ερωτήματα!
Στέκουν και αυτόνομα. -
Καλημέρα Διονύση. Εξόχως διδακτική! Ιδιαίτερα το iii ερώτημα που εμπλέκεται και η Γεωμετρία!
Να είσαι πάντα καλά. -
Καλημέρα συνάδελφοι.
Γιάννη και Πρόδρομε σας ευχαριστώ για το σχολιασμό
Πρόδρομε, μιλώντας για Γεωμετρία, νομίζω φανέρωσες και το λόγο που άρεσε και στο Γιάννη 🙂
Η Γεωμετρία είναι η αιτία!!! -
Αντίθετα Διονύση. Είναι καλόγουστη και δεν διολισθαίνει στη Γεωμετρία έχοντας τη Φυσική σαν πρόφαση.
Η δεύτερη οδός (η διολίσθηση) είναι η εύκολη τελικά και ένα σύμπτωμα τα τελευταία χρόνια. -
Δηλαδή άλλο να χρησιμοποιείς γεωμετρικές γνώσεις και άλλο να μετατρέπεις ασκήσεις Γεωμετρίας σε ασκήσεις Ηλεκτρομαγνητισμού.
-
Συμφωνώ Γιάννη, ότι πρέπει να μελετάμε Φυσική με την βοήθεια Γεωμετρίας και όχι να εξασκούμαστε στη Γεωμετρία με πρόφαση τη Φυσική.
-
Ας κάνω το αντίθετο από σένα σε μια παιγνιώδη ανάρτηση που κάνει Γεωμετρία με πρόφαση τη Φυσική. Θα ονομασθεί:
Βρείτε το μαγνητικό πεδίο. -
Νομίζω ότι οφείλω μια διευκρίνηση, πάνω σε ένα σημείο στο ερώτημα ii) που μου επεσήμανε φίλος, σε μήνυμα του.
“Δεν μπορεί η ένταση του πεδίου, σε ένα σημείο πάνω στην ακτίνα ΟΡ, εξαιτίας του αγωγού (1) να βρίσκεται πάνω στην ακτίνα, οπότε μηδενίζετααι το γινόμενο BΔlσυνφ”;
Ναι αυτό μπορεί να συμβεί, αλλά μόνο για ένα στοιχειώδες τμήμα Δl πάνω στην ακτίνα.
Αλλά δεν ζητάει αυτό το ερώτημα. Ζητάει το άθροισμα για όλα τα Δl, κατά μήκος της ακτίνας. Και αν για ένα τέτοιο τμήμα η γωνία μεταξύ Δl και Β είναι π/2, για όλα τα άλλα η γωνία είναι αμβλεία και συνφ<0, οπότε και η κυκλοφορία θα προκύψει αρνητική. -
Καλημέρα και καλή εβδομάδα.
Διονύση την έχω δει από εχθές αλλά δεν είχα χρόνο να σχολιάσω.
Οι ασκήσεις με την εύρεση των εντάσεων των Μ.Π. σε σημεία στην κοντινή περιοχή των αγωγών μπορούν να δώσουν ωραίους προβληματισμούς. Χρειάζονται τόσο την γεωμέτρια όσο και τη δυνατότητα χειρισμών που αφορούν τα διανύσματα.
Μου άρεσε και το ερώτημα που σχετίζεται με το νόμο του Ampere μιας και δεν χρειάζεται ιδιαίτερα δύσκολη σκέψη για να απαντηθεί .
Να είσαι καλά!
-
Καλημέρα Κώστα.
Ευχαριστώ για το σχολιασμό.
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 4 μέρες
Ένα εύκολο κουίζ στις ταλαντώσεις.
 Το σώμα κρέμεται από το ταβάνι με ελατήριο. Η ιδιοσυχνότητα του ταλαντωτή είναι ωο. Το πιάνουμε με το χέρι και το αναγκάζουμε να εκτελεί αρμον […]
Το σώμα κρέμεται από το ταβάνι με ελατήριο. Η ιδιοσυχνότητα του ταλαντωτή είναι ωο. Το πιάνουμε με το χέρι και το αναγκάζουμε να εκτελεί αρμον […]-
Αφιερωμένη στον Θοδωρή που έριξε την ιδέα με την ανάρτησή του τη σχετική με τα όρια μοντελοποίησης.
-
Ευχαριστώ Γιάννη, εννοείς αν καταλαβαίνω σωστά πλάτη Α1, Αο , Α2 για ω1, ωο, ω2…
ή εννοείς Α ασχέτως γωνιακής συχνότητας; -
Το δεύτερο. Δεδομένο πλάτος Α.
Κουνάω το χέρι μου όπως θέλω. -
Υπάρχει διαφορά αν το χέρι πιάνει την πάνω άκρη του ελατηρίου.
Τότε το χέρι ταλαντεύεται με πλάτος 2 πόντους και προκαλεί πλάτος 20 πόντους στον συντονισμό και 10 πόντους σε άλλη συχνότητα.
Όταν το χέρι κρατάει το σώμα τότε το πλάτος της ταλάντωσης είναι το ίδιο. -
Γιάννη, γιατί βλέπω ίδια ενέργεια, σε κάθε περίπτωση;
Αν το χέρι σου δίνει κάποια ενέργεια, πρέπει κάπου να την αναζητήσουμε.
Αν εξαιρέσουμε την πρώτη ταλάντωση που το σύστημα κερδίζει ενέργεια 1/2 KA^2, ϊδια και για τις τρεις ταλαντώσεις, από κει και πέρα θερμότητα δεν βλέπω να παράγεται, ούτε κάποια άλλη μετατροπή ενέργειας βλέπω.
Κάνω λάθος; -
Διονύση αν η απόσβεση είναι μηδέν δεν προσφέρουμε.ενέργεια. Η ερώτηση έχει νόημα μόνο αν υπάρχει απόσβεση με συντελεστή b. Σε κάθε ρεαλιστική περίπτωση έχουμε απόσβεση.
-
Δηλαδή ψάχνουμε για το έργο W=πbωΑ^2;
-
Δεν είναι δεύτερο θέμα αλλά αφορμή για συζήτηση πάνω στην εξαναγκασμένη και τον συντονισμό.
-
Ναι γι αυτό σε μία περίοδο και κάτι ανάλογο σε δεδομένο διάστημα. Γράφαμε μαζί.
-
Μια απάντηση προστέθηκε.
Τίθεται το ερώτημα αν μπορούμε να μιλάμε για εξαναγκασμένη ταλάντωση και συντονισμό.
Η σχέση με την ανάρτηση του Θοδωρή προφανής. -
Γιαννη τωρα ειδα οτι εβαλες απαντηση θα την δω
-
Καλησπέρα Κωνσταντίνε.
Ναι όσο μεγαλύτερη η συχνότητα τόσο μεγαλύτερη η προσφερόμενη ενέργεια.
Έχω γράψει μια λύση μετά την εκφώνηση. -
Καλησπερα σε ολους.Εδω εχουμε τρεις δυναμεις ,βαρος χερι ελατηριο. Οι δυο ειναι συντηρητικες αρα ειναι σαν να μην υπαρχουν αφου εχουν εργομηδεν ανα περιοδο. Αρα εχουμε μονο το χερι μας. Ο ορος ιδιοσυχνοτητα εδω δεν νομιζω οτι παιζει ρολο,κουναμε απλως ενα σωμα μεσα σε ενα ρευστο και τρεις συχνοτητες διατεταγμενες.Προφανως για οσο περισσοτερο χρονο το κουναμε ,τοσο πιο πολυ εργο παραγουμε. Αρα με την μεγαλη συχνοτητα.Αν η δυναμη αποσβεσης ειναι αναλογη του τετραγωνου της ταχυτητας τοτε και ανα περιοδο παραγουμε περισσοτερο εργο.
-
Αν η δυναμη αποσβεσης ηταν αναλογη του ριζαυ?
-
Τότε αλλάζουν οι μαθηματικοί υπολογισμοί (δυσκολότεροι) αλλά παραμένει η ίδια ουσία:
Μεγαλύτερη συχνότητα => μεγαλύτερες ταχύτητες στην ίδια θέση => μεγαλύτερες δυνάμεις απόσβεσης στην ίδια θέση =>μεγαλύτερες απώλειες. -
Θα συμφωνήσω με το τελικό συμπέρασμα που καταλήγεις Γιάννη.
Αυτή δεν είναι η γνωστή μας εξαναγκασμένη ταλάντωση και δεν μπορούμε να την αντιμετωπίζουμε΄σαν την γνωστή μας κυρία 🙂 και να καταλήγουμε στα γνωστά συμπεράσματα από την θεωρία…
Ούτε συντονισμό έχουμε, ούτε τίποτα από τα γνωστά.
Και να το πάω και ένα βήμα παραμέρα; Το ότι κρατώ ένα δίσκο με το χέρι μου και τον κινώ πάνω – κάτω, δεν σημαίνει ότι έχουμε τη γνωστή μας ΑΑΤ με δυναμική ενέργεια κλπ…, έστω και αν η απομάκρυνση είναι αρμονική συνάρτηση του χρόνου. -
Συμφωνώ σε όλα και φυσικά για τα σχετικά με δυναμική ενέργεια.
Ξαναδές το ερέθισμα:
https://i.ibb.co/k2YtFYYw/33.pngΤί σόι συντονισμός είναι αυτός;
-
Γιάννη, έγραψα δίπλα:
Άστο καλύτερα…
Προφανώς θέλω να πω ότι όλο αυτό το ευφάνταστο σενάριο, ξέφυγε και δεν χρειάζεται να μας απασχολεί… -
Απλως σκεφτομαι το εξης. Αν η συχνοτητα μεγαλωνει,τοτε προφανως η περιοδος μικραινει αρα ανα περιοδο το εργο που προσφερουμε ειναι μικροτερο διοτι κινουμαστε για λιγοτερο χρονο.Ομως οι ταχυτητες μεγαλωνουν οποτε η δυναμη αποσβεσης μεγαλωνει και το εργο που προσφερουμε ανα περιοδο μεγαλωνει. Ποιο απο τα δυο υπερισχυει? Αυτο προφανως εξαρταται απο το με ποια δυναμη της ταχυτητας ειναι αναλογη η αποσβεση. Δ εν ξερω αν ακαταλαβες τι θελω να πω.
-
Διονύση η πρόθεση του κατασκευαστή του θέματος ίσως ήταν να δει αν ξέρει ο μαθητής να υπολογίσει τη συχνότητα από ταχύτητα και μήκος κύματος και ακόμα αν ξέρει πόση είναι η ιδιοσυχνότητα.
Μια διόρθωση θα ήταν “Ταλαντώνεται με συχνότητα ίση με την ιδιοσυχνότητά του”.
Χωρίς αναφορές σε συντονισμό. -
Κατάλαβα Κωνσταντίνε.
Πάντως η ισχύς αντίστασης θα έχει εκθέτη μεγαλύτερο της μονάδας.
Στην περίπτωση που προανέφερες 3/2. -
Καλησπέρα σας
Γιάννη ενδιαφέρον θέμα
Μια εξέταση για διάφορες δυνάμεις απόσβεσης:
https://i.ibb.co/fdh5vD5y/page-0001.jpg -
Ωραίο Χρήστο!
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 1 εβδομάδα, 5 μέρες
Μεταβολές με το κλείσιμο του διακόπτη.
 Στο διπλανό κύκλωμα, με τον διακόπτη δ ανοικτό, ο αντιστάτης R διαρρέεται από ρεύμα έντασης Ι και πάνω παράγεται θερμότητα με ρυθμό Ρ. Αν κλείσουμε το […]
Στο διπλανό κύκλωμα, με τον διακόπτη δ ανοικτό, ο αντιστάτης R διαρρέεται από ρεύμα έντασης Ι και πάνω παράγεται θερμότητα με ρυθμό Ρ. Αν κλείσουμε το […]-
Καλησπέρα Διονύση. Πολύ καλή.
Ας υποθέσουμε ότι η ίδια άσκηση βρίσκεται στη Γ΄και αντί για 2 αντιστάσεις έχει δυο σωληνοειδή, μετά τη μεταβατική κατάσταση. Τότε θα “πλακωθούν” να τη λύσουν οι μαθητές γιατί είναι στην ύλη των Πανελλαδικών! Η μελέτη όμως του κυκλώματος στο ηλεκτρικό ρεύμα πρέπει να έχει γίνει στον καιρό της, δηλαδή στη Β΄τάξη. Αλλιώς βράσε ρύζι. -
Καλημέρα Ανδρέα και καλή Κυριακή.
Λες να αντικαταστήσω τους αντιστάτες με πηνία για… να πουλήσει το προϊόν; 🙂 -
https://i.ibb.co/ksqc2Lhz/Ohm.png
Αν το έβλεπα “ξέμπαργκο” δεν θα το αναγνώριζα…
Η μείωση της ισχύος στον αντιστάτη R νομίζω Διονύση, πως πρέπει να αναφερθεί
σε αντιδιαστολή με την αύξηση της ισχύος που δίνει η πηγή…Και ένα σωληνοειδές παράλληλα σε αντιστάτη φθάνει Ανδρέα
-
Καλημέρα Θοδωρή και σε ευχαριστώ για το σχολιασμό.
Και γω αν έβλεπα την εξίσωσή σου, στο ξεκάρφωτο, θα ξαφνιαζόμουν!
Εξάλλου δεν την έγραψα στην απάντηση, αφού δεν έχουμε ανάγκη από μια ακόμη εξίσωση, αλλά ευλυγισία, ώστε να εφαρμόζουμε το νόμο του Οhm, για μια αντίσταση, όπως και το νόμο του Οhm για κλειστό κύκλωμα… -
Καλημέρα Παντελή, σε ευχαριστώ για το σχολιασμό.
Το “μεταφορικό μέσον” τάση, είναι ένας ισοδύναμος άλλος τρόπος για να φτάσει κάποιος στα κατάλληλα συμπεράσματα.
Να είσαι καλά. -
Καλημέρα Διονύση της ΓΠ!
Χρησιμοποιώντας άλλο …μεταφορικό μέσο
https://i.ibb.co/DHCqwKbT/R.png
https://i.ibb.co/v4Sk8Wj5/2026-01-26-120413.png
Καλή εβδομάδα
-
-
H/o Γιάννης Κυριακόπουλος έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες
Η πιθανότητα για την απόσταση δύο ταλαντωτών.
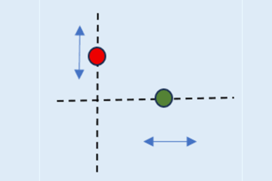 Η εξίσωση θέσης του κόκκινου ταλαντωτή είναι y = ημt. Του πράσινου είναι x = 2 + συνt. Ποια είναι η πιθανότητα να απέχουν οι δύο ταλαντωτές απόσταση μικρότερη από ρίζα(3) m ; Δυο απαντήσεις:
Η εξίσωση θέσης του κόκκινου ταλαντωτή είναι y = ημt. Του πράσινου είναι x = 2 + συνt. Ποια είναι η πιθανότητα να απέχουν οι δύο ταλαντωτές απόσταση μικρότερη από ρίζα(3) m ; Δυο απαντήσεις:-
Καλησπερα Γιαννη. Ωραιο ερωτημα. Αυτο που εχει το μεγαλυτερο ενδιαφερον ειναι πως αν δεις μια μεθοδο, μπορεις να την κανεις εργαλειο σου και να την χρησιμοποιησεις στο μελλον. Aυτο σημαινει μαθαινω.Ετσι εχοντας δει την μεθοδο στο Ο μέγιστος ρυθμός αύξησης της απόστασης. oπου ο ενας βλεπει τον αλλον να γραφει κυκλο,μπορεσα και ελυσα και αυτην,με τον δευτερο τροπο σου 🙂
-
Καλησπέρα Κωνσταντίνε.
Ευχαριστώ.
-
-
H/o Διονύσης Μάργαρης έγραψε ένα νέο άρθρο πριν από 2 εβδομάδες
Μια ερώτηση στο νόμο Biot-Savart.
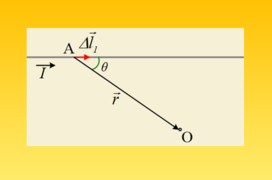 Στο σχήμα ένας ευθύγραμμος ρευματοφόρος αγωγός, μεγάλου μήκους, διαρρέεται από ρεύμα έντασης Ι. Έστω ένα μικρό τμήμα Δl1, του αγωγού αυτού στη θέση Α, εξαιτ […]
Στο σχήμα ένας ευθύγραμμος ρευματοφόρος αγωγός, μεγάλου μήκους, διαρρέεται από ρεύμα έντασης Ι. Έστω ένα μικρό τμήμα Δl1, του αγωγού αυτού στη θέση Α, εξαιτ […]-
Καλό μεσημέρι Διονύση.
Απλό και ωραίο για εξετάσεις.
Μια ερώτηση να κάνω: πέραν της μεγιστοποίησης του ημθ ,
δεν πρέπει να αναφερθούμε στη σύγχρονη ελαχιστοποίηση της r
που συνηγορεί για max και που βέβαια είναι συνεπακόλουθο;
Να είσαι πάντα καλά -
Καλό απόγευμα Παντελή και σε ευχαριστώ για το σχολιασμό.
Έχεις βέβαια δίκιο για την ελάχιστη απόσταση και γι΄ αυτό άλλωστε τελικά προκύπτει και ο οκταπλασιασμός της έντασης, διαφορετικά θα μέναμε στον διπλασιασμό της.
Κάνω την προσθήκη. -
Διονύση, καλησπέρα (χαθήκαμε). Καλή χρονιά (αν δεν τα ξαναείπαμε).
Πολύ καλή ως Β θέμα.
Αν και από τη σχέση του Β το πηλίκο (ημθ/r^2) φαίνεται εύκολα ότι αυξάνεται καθώς το Δl μετατοπίζεται δεξιότερα (αύξηση αριθμητή και μείωση παρανομαστή), νομίζω ότι προτιμότερο θα ήταν μια αλλαγή του r με d/ημθ, οπότε καταλήγουμε σε μια σχέση του Β με (ημ^3/d^2), δηλ. με μια μόνο μεταβλητή (το ημ^3). -
Καλησπέρα Ντίνο και καλή χρονιά.
Ο κύβος του ημιτόνου, προέκυψε στην μαθηματική επεξεργασία για την ένταση, στη λύση.
Η αρχική διατύπωση με λόγια, είναι μια ποιοτική πρώτη ερμηνεία, χωρίς επεξεργασία, απλά ερμηνεύοντας την εξίσωση που δίνει το νόμο των B-S.
-
- Φόρτωσε Περισσότερα
Αφιερωμένη στον Παύλο Αλεξόπουλο, ο οποίος προηγήθηκε χρονικά με ανάλογο θέμα…
Καλημέρα. Διονύση σε ευχαριστώ πολύ για την αφιέρωση, η άσκηση είναι εξαιρετική!